Which Is Greater 3/4 Or 1/2
pythondeals
Nov 26, 2025 · 10 min read
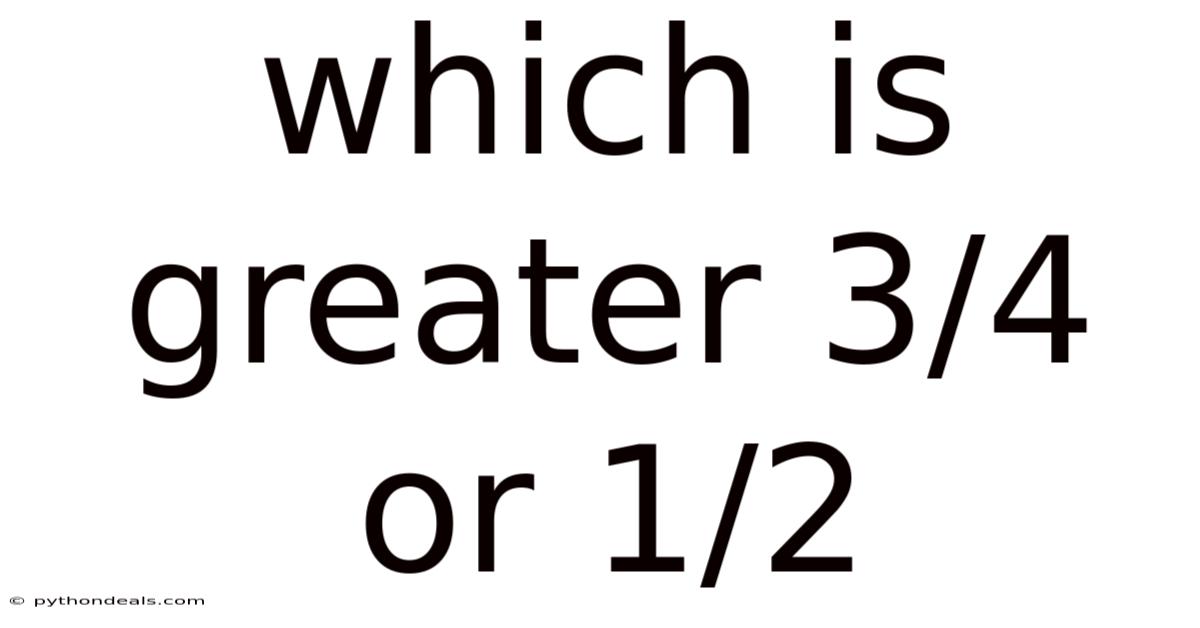
Table of Contents
Let's embark on a mathematical journey to definitively answer the age-old question: which is greater, 3/4 or 1/2? At first glance, these fractions might seem deceptively similar. However, delving into their fundamental meanings and employing a variety of comparison methods will reveal a clear and undeniable victor. This article will not only provide the straightforward answer but will also illuminate the underlying mathematical principles that make the conclusion irrefutable. We'll cover everything from basic definitions to advanced comparison techniques, ensuring a thorough understanding for readers of all backgrounds. So, buckle up and prepare to explore the fascinating world of fractions!
Fractions, at their core, represent parts of a whole. The fraction a/b (where a and b are integers, and b is not zero) signifies that a whole has been divided into b equal parts, and we are considering a of those parts. Understanding this fundamental definition is crucial to grasping the magnitude and relationship between different fractions. Now, with this baseline understanding, we can delve into comparing 3/4 and 1/2.
Demystifying Fractions: A Comprehensive Overview
Before we directly compare 3/4 and 1/2, it's essential to solidify our understanding of what fractions represent and the ways we can manipulate them. This section will cover key aspects of fractions, including their definition, different types, and basic operations.
What is a Fraction?
As briefly mentioned above, a fraction represents a part of a whole. It is written as a/b, where:
- a is the numerator, representing the number of parts we are considering.
- b is the denominator, representing the total number of equal parts the whole has been divided into.
For example, if we have a pizza cut into 8 slices and we eat 3 slices, we have eaten 3/8 of the pizza.
Types of Fractions
Fractions can be categorized into several types:
- Proper Fractions: The numerator is less than the denominator (e.g., 1/2, 3/4, 5/8). These fractions represent a value less than 1.
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 4/3, 5/5, 7/2). These fractions represent a value greater than or equal to 1.
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 1/2, 2 3/4). Mixed numbers are essentially another way to represent improper fractions. For example, 1 1/2 is equivalent to 3/2.
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 2/4).
Basic Operations with Fractions
Understanding how to perform basic operations (addition, subtraction, multiplication, and division) with fractions is crucial for comparing them.
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator. For example, to add 1/2 and 1/4, we convert 1/2 to 2/4, resulting in 2/4 + 1/4 = 3/4.
-
Multiplication: To multiply fractions, simply multiply the numerators and the denominators: (a/b) * (c/d) = (ac) / (bd). For example, 1/2 * 3/4 = 3/8.
-
Division: To divide fractions, multiply the first fraction by the reciprocal of the second fraction: (a/b) / (c/d) = (a/b) * (d/c) = (ad) / (bc). For example, 1/2 / 3/4 = 1/2 * 4/3 = 4/6 = 2/3.
With these foundational concepts in place, we can now proceed to directly compare 3/4 and 1/2 using various methods.
Comparing Fractions: The Techniques Unveiled
Several methods can be employed to compare fractions, each offering a slightly different perspective and level of clarity. We will explore three of the most common and effective methods:
-
Finding a Common Denominator: This is perhaps the most intuitive and widely used method. The idea is to convert both fractions to equivalent fractions with the same denominator. Once the denominators are the same, comparing the numerators becomes straightforward.
-
Converting to Decimals: Every fraction can be expressed as a decimal by dividing the numerator by the denominator. Comparing decimals is often easier than comparing fractions directly, especially for those more comfortable with decimal representation.
-
Cross-Multiplication: This is a shortcut method that directly compares the products of the numerator of one fraction and the denominator of the other. The larger product indicates the larger fraction.
Let's apply each of these methods to our specific problem: comparing 3/4 and 1/2.
1. Finding a Common Denominator
The least common multiple (LCM) of 4 and 2 is 4. Therefore, we want to convert both fractions to have a denominator of 4.
-
3/4 already has the desired denominator.
-
To convert 1/2 to an equivalent fraction with a denominator of 4, we multiply both the numerator and denominator by 2: (1 * 2) / (2 * 2) = 2/4.
Now we can directly compare 3/4 and 2/4. Since 3 is greater than 2, we can conclude that 3/4 is greater than 2/4, and therefore 3/4 is greater than 1/2.
2. Converting to Decimals
To convert a fraction to a decimal, we simply divide the numerator by the denominator.
-
3/4 = 3 ÷ 4 = 0.75
-
1/2 = 1 ÷ 2 = 0.5
Comparing the decimals, we see that 0.75 is greater than 0.5. Therefore, 3/4 is greater than 1/2.
3. Cross-Multiplication
To cross-multiply, we multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
-
3/4 vs. 1/2
-
3 * 2 = 6
-
1 * 4 = 4
Since 6 is greater than 4, we can conclude that 3/4 is greater than 1/2.
Conclusion from Comparison Methods
All three methods consistently demonstrate that 3/4 is greater than 1/2. This provides a robust confirmation of our initial hypothesis.
Real-World Applications: Why Fraction Comparison Matters
The ability to compare fractions extends far beyond the realm of abstract mathematics. It's a practical skill with numerous applications in everyday life and various professional fields.
Everyday Life Examples
- Cooking and Baking: Recipes often use fractional measurements. Knowing how to compare fractions allows you to easily adjust recipes, double or halve ingredients, or determine which container is larger. For example, if a recipe calls for 2/3 cup of flour and you only have a 1/2 cup measuring cup, you need to understand that 2/3 is greater than 1/2 to adjust accordingly.
- Shopping and Sales: Comparing discounts expressed as fractions or percentages (which are essentially fractions) helps you determine which deal offers the best savings. For instance, a 1/4 off sale compared to a 1/5 off sale requires you to know that 1/4 is greater than 1/5 to choose the better deal.
- Time Management: Breaking down tasks into fractional components of time allows for better planning and prioritization. Comparing fractions of time helps you allocate resources efficiently. For example, if you need to spend 1/3 of your day on work and 1/4 of your day on errands, knowing that 1/3 is greater than 1/4 helps you allocate more time to work.
- Sharing and Dividing: Dividing resources or tasks fairly often involves fractions. Comparing fractions ensures equitable distribution. For instance, dividing a pizza among friends requires an understanding of fractions to ensure everyone gets a fair share.
- Understanding Data and Statistics: Fractions are often used to represent proportions and ratios in data analysis. Comparing these fractions provides insights into trends and relationships. For example, if 3/5 of students prefer math and 2/5 prefer science, knowing that 3/5 is greater than 2/5 allows you to understand the overall preference.
Professional Applications
- Finance: Comparing interest rates, investment returns, and debt ratios often involves working with fractions and percentages. Financial analysts need to accurately compare these values to make informed decisions.
- Engineering: Calculating material strengths, load distributions, and tolerances often requires precise calculations with fractions. Engineers rely on accurate comparisons to ensure structural integrity.
- Science: Experiments often involve measuring and comparing fractional quantities. Scientists need to understand these values to interpret results and draw conclusions.
- Construction: Measuring dimensions, calculating material requirements, and estimating project costs all involve working with fractions. Construction workers need to be proficient in fraction comparison to ensure accurate and efficient project execution.
- Medicine: Dosage calculations, interpreting lab results, and understanding statistical data often require a strong understanding of fractions. Medical professionals rely on these skills to provide accurate diagnoses and treatments.
These examples illustrate the pervasive nature of fractions and the importance of being able to compare them accurately and efficiently. Whether it's in the kitchen, the boardroom, or the laboratory, a solid understanding of fractions is an invaluable asset.
Addressing Common Misconceptions
Despite the relatively simple nature of fraction comparison, several common misconceptions can lead to errors and confusion. Addressing these misconceptions is crucial for developing a deeper and more accurate understanding of fractions.
Misconception 1: Larger Denominator Means Larger Fraction
A common mistake is to assume that a fraction with a larger denominator is always greater than a fraction with a smaller denominator. This is incorrect. The denominator represents the number of parts the whole is divided into. A larger denominator means the whole is divided into more parts, making each individual part smaller. For example, 1/10 is smaller than 1/2, even though 10 is greater than 2.
Misconception 2: Focusing Only on the Numerator
Another error is to only consider the numerator when comparing fractions. While the numerator does represent the number of parts we are considering, it's meaningless without considering the size of those parts, which is determined by the denominator. For example, 5/10 is smaller than 1/2 (which is equivalent to 5/10), even though the numerators are equal.
Misconception 3: Difficulty with Improper Fractions and Mixed Numbers
Some students struggle to compare improper fractions or mixed numbers. It's important to remember that improper fractions represent values greater than or equal to 1, and mixed numbers are simply another way to represent improper fractions. To compare them, either convert them to equivalent fractions with a common denominator or convert them to decimals.
Misconception 4: Incorrectly Applying Cross-Multiplication
Cross-multiplication is a useful shortcut, but it can be misused if not applied correctly. Remember that the larger product indicates the larger fraction. It's easy to get confused and incorrectly associate the larger product with the smaller fraction.
How to Avoid Misconceptions
- Visual Aids: Using visual aids like pie charts or number lines can help students visualize fractions and understand their relative sizes.
- Real-World Examples: Connecting fractions to real-world examples makes the concepts more concrete and relatable.
- Practice and Repetition: Regular practice with various fraction comparison problems reinforces the concepts and helps identify and correct misconceptions.
- Focus on the Meaning: Emphasize the underlying meaning of fractions as parts of a whole, rather than just memorizing rules and procedures.
By addressing these common misconceptions and promoting a deeper understanding of fractions, we can empower students and individuals to confidently navigate the world of fractional quantities.
Conclusion: The Verdict is In!
After thorough examination and employing multiple comparison methods, the answer is clear: 3/4 is greater than 1/2. This conclusion is supported by finding a common denominator, converting to decimals, and using cross-multiplication. Understanding the fundamental principles of fractions and mastering the techniques for comparing them is crucial for success in mathematics and in everyday life.
The journey through the world of fractions doesn't have to end here. There are always new mathematical landscapes to explore and discoveries to be made. What other fractional comparisons intrigue you? Are you interested in exploring more complex operations with fractions, such as simplifying or converting between fractions, decimals, and percentages? The world of mathematics awaits!
Latest Posts
Latest Posts
-
How To Find Lsrl On Ti 84
Nov 26, 2025
-
When To Use Independent T Test
Nov 26, 2025
-
Which Is Greater 3 4 Or 1 2
Nov 26, 2025
-
How To Sketch An Angle In Standard Position
Nov 26, 2025
-
How To Solve Ordinary Differential Equations
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about Which Is Greater 3/4 Or 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.