Which Is Greater 3/4 Or 5/8
pythondeals
Nov 20, 2025 · 8 min read
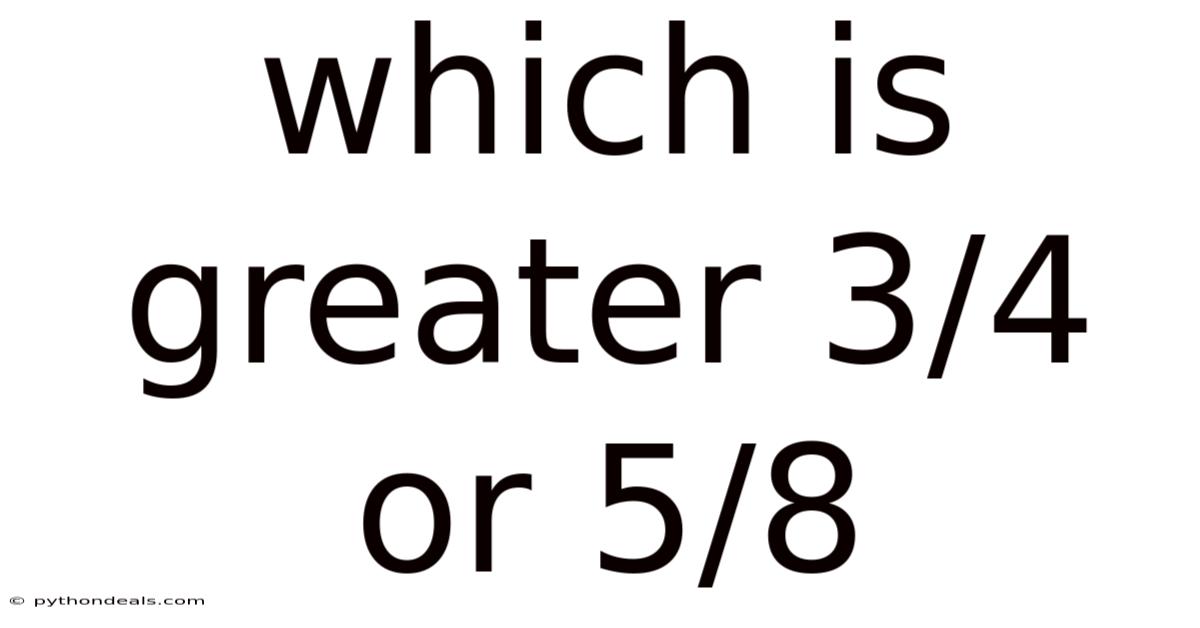
Table of Contents
Let's embark on a journey to unravel a common mathematical puzzle: determining which fraction is greater, 3/4 or 5/8. This seemingly simple comparison forms the foundation of more complex mathematical operations and is crucial for everyday problem-solving. Understanding how to compare fractions not only sharpens your math skills but also enhances your critical thinking abilities.
Fractions are an integral part of our daily lives, appearing in recipes, measurements, and financial transactions. Knowing how to accurately compare them ensures that we make informed decisions and avoid errors. This article will delve into several methods to compare these fractions, providing clear, step-by-step instructions to help you master this skill.
Understanding Fractions
Before diving into the comparison of 3/4 and 5/8, let's briefly revisit what fractions represent. A fraction consists of two parts: the numerator (the number above the line) and the denominator (the number below the line). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts that make up a whole.
For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 parts out of a total of 4 equal parts. Similarly, in the fraction 5/8, the numerator is 5, and the denominator is 8, meaning we have 5 parts out of a total of 8 equal parts.
Method 1: Finding a Common Denominator
One of the most straightforward methods to compare fractions is by finding a common denominator. The common denominator is a number that both denominators can divide into evenly. Once both fractions have the same denominator, it becomes easier to compare them simply by looking at their numerators.
Step-by-Step Instructions
- Identify the Denominators: In our case, the denominators are 4 and 8.
- Find the Least Common Multiple (LCM): The LCM of 4 and 8 is the smallest number that both 4 and 8 can divide into without leaving a remainder. The multiples of 4 are 4, 8, 12, 16, and so on. The multiples of 8 are 8, 16, 24, 32, and so on. The smallest number that appears in both lists is 8, so the LCM is 8.
- Convert the Fractions: Now, we need to convert both fractions to have the common denominator of 8.
- For 3/4, we need to multiply both the numerator and the denominator by the same number so that the denominator becomes 8. Since 4 multiplied by 2 equals 8, we multiply both the numerator and the denominator by 2:
(3 * 2) / (4 * 2) = 6/8 - For 5/8, the denominator is already 8, so we don't need to change this fraction.
- For 3/4, we need to multiply both the numerator and the denominator by the same number so that the denominator becomes 8. Since 4 multiplied by 2 equals 8, we multiply both the numerator and the denominator by 2:
- Compare the Numerators: Now that both fractions have the same denominator, we can compare their numerators. We have 6/8 and 5/8. Since 6 is greater than 5, 6/8 is greater than 5/8.
- Conclusion: Therefore, 3/4 (which is equivalent to 6/8) is greater than 5/8.
Method 2: Cross-Multiplication
Cross-multiplication is a quick and efficient method to compare two fractions without needing to find a common denominator. This method involves multiplying the numerator of one fraction by the denominator of the other and comparing the results.
Step-by-Step Instructions
- Write Down the Fractions: We have 3/4 and 5/8.
- Cross-Multiply:
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (8):
3 * 8 = 24 - Multiply the numerator of the second fraction (5) by the denominator of the first fraction (4):
5 * 4 = 20
- Multiply the numerator of the first fraction (3) by the denominator of the second fraction (8):
- Compare the Results: Compare the two products obtained from cross-multiplication.
- We have 24 and 20.
- Since 24 is greater than 20, the first fraction (3/4) is greater than the second fraction (5/8).
- Conclusion: Therefore, 3/4 is greater than 5/8.
Method 3: Converting to Decimals
Another effective method to compare fractions is by converting them into decimal form. This involves dividing the numerator by the denominator to obtain a decimal value. Once both fractions are in decimal form, comparing them becomes straightforward.
Step-by-Step Instructions
- Convert 3/4 to a Decimal: Divide 3 by 4.
3 ÷ 4 = 0.75
- Convert 5/8 to a Decimal: Divide 5 by 8.
5 ÷ 8 = 0.625
- Compare the Decimals: Compare the decimal values obtained.
- We have 0.75 and 0.625.
- Since 0.75 is greater than 0.625, 3/4 is greater than 5/8.
- Conclusion: Therefore, 3/4 is greater than 5/8.
Method 4: Visual Representation
Visual representation can often provide an intuitive understanding of fraction comparison. By drawing diagrams, you can visually see which fraction represents a larger portion of a whole.
Step-by-Step Instructions
- Draw Two Identical Rectangles: Represent each fraction with a rectangle of the same size.
- Divide the First Rectangle into Four Equal Parts: Since the denominator of 3/4 is 4, divide the first rectangle into four equal parts. Shade three of these parts to represent 3/4.
- Divide the Second Rectangle into Eight Equal Parts: Since the denominator of 5/8 is 8, divide the second rectangle into eight equal parts. Shade five of these parts to represent 5/8.
- Compare the Shaded Areas: Visually compare the shaded areas in both rectangles. You will notice that the shaded area in the rectangle representing 3/4 is larger than the shaded area in the rectangle representing 5/8.
- Conclusion: Therefore, 3/4 is greater than 5/8.
Real-World Applications
Understanding how to compare fractions is not just a theoretical exercise; it has numerous real-world applications. Here are a few examples:
- Cooking: When following a recipe, you might need to adjust ingredient quantities. For instance, if a recipe calls for 3/4 cup of flour, but you only have a 5/8 cup measuring tool, you need to know which amount is greater or if you need to add more.
- Construction: In construction, measurements often involve fractions. Comparing fractions ensures that materials are cut to the correct size and that structures are built accurately.
- Finance: When dealing with investments or loans, interest rates are often expressed as fractions or percentages, which are essentially fractions. Comparing these rates helps you make informed financial decisions.
- Shopping: Discounts are frequently expressed as fractions or percentages. Knowing how to compare these values allows you to determine which offers the best savings.
Common Mistakes to Avoid
When comparing fractions, it's easy to make mistakes if you're not careful. Here are some common errors to avoid:
- Comparing Numerators Directly Without a Common Denominator: This is a frequent mistake. You cannot accurately compare fractions unless they have the same denominator. For example, you can't simply say that 5/8 is greater than 3/4 because 5 is greater than 3.
- Incorrectly Finding the Least Common Multiple: A wrong LCM will lead to incorrect conversions and, consequently, a wrong comparison. Always double-check your LCM calculations.
- Arithmetic Errors: Mistakes in multiplication or division can lead to incorrect results. Take your time and double-check your calculations.
- Misinterpreting Visual Representations: Ensure that your visual representations are accurate and to scale. Otherwise, you might draw the wrong conclusion.
Advanced Techniques
For more complex fractions or when dealing with a large number of fractions, more advanced techniques might be necessary.
- Using Prime Factorization to Find the LCM: Prime factorization involves breaking down each denominator into its prime factors. This can be particularly useful for finding the LCM of larger numbers.
- Using Calculators or Software: Modern calculators and software tools can quickly convert fractions to decimals and compare them. These tools are particularly helpful in professional settings where accuracy and speed are essential.
Historical Context
The concept of fractions dates back to ancient civilizations. The Egyptians and Babylonians used fractions in their systems of measurement and accounting. The Egyptians, for example, used unit fractions (fractions with a numerator of 1) extensively. The Babylonians, on the other hand, used a base-60 system, which made dealing with fractions relatively straightforward.
The development of modern fractional notation and techniques for comparing fractions evolved over centuries. Mathematicians like Fibonacci played a crucial role in popularizing the use of fractions in Europe.
FAQ Section
Q: Why is it important to find a common denominator when comparing fractions?
A: Finding a common denominator ensures that you are comparing fractions with equal-sized parts. This allows you to accurately compare the numerators and determine which fraction represents a larger portion of the whole.
Q: Can I always use cross-multiplication to compare fractions?
A: Yes, cross-multiplication is a reliable method for comparing two fractions. However, it's essential to remember that this method only works for comparing two fractions at a time.
Q: Is converting to decimals always the best method for comparing fractions?
A: Converting to decimals can be a quick and accurate method, especially when using a calculator. However, some fractions result in repeating decimals, which can make comparison slightly more challenging.
Q: What if I need to compare more than two fractions?
A: If you need to compare more than two fractions, the easiest approach is to find a common denominator for all the fractions and then compare the numerators. Alternatively, you can convert all the fractions to decimals and compare the decimal values.
Conclusion
Comparing fractions is a fundamental skill with widespread applications in everyday life. Whether you choose to find a common denominator, use cross-multiplication, convert to decimals, or use visual representations, the key is to understand the underlying principles and practice regularly.
In the case of 3/4 and 5/8, we have demonstrated through multiple methods that 3/4 is indeed greater than 5/8. Mastering these techniques will not only enhance your mathematical abilities but also empower you to make more informed decisions in various real-world scenarios.
How do you prefer to compare fractions, and what other mathematical concepts would you like to explore further?
Latest Posts
Latest Posts
-
Which Class Of Elements Best Conducts Electricity
Nov 20, 2025
-
How Does A Mutation Affect A Protein
Nov 20, 2025
-
How To Find 95 Confidence Interval On Excel
Nov 20, 2025
-
Cathode And Anode X Ray Tube
Nov 20, 2025
-
Find Eigenvalues And Eigenvectors Of A 3x3 Matrix
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about Which Is Greater 3/4 Or 5/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.