What Is The Derivative Of Sin X 2
pythondeals
Nov 10, 2025 · 8 min read
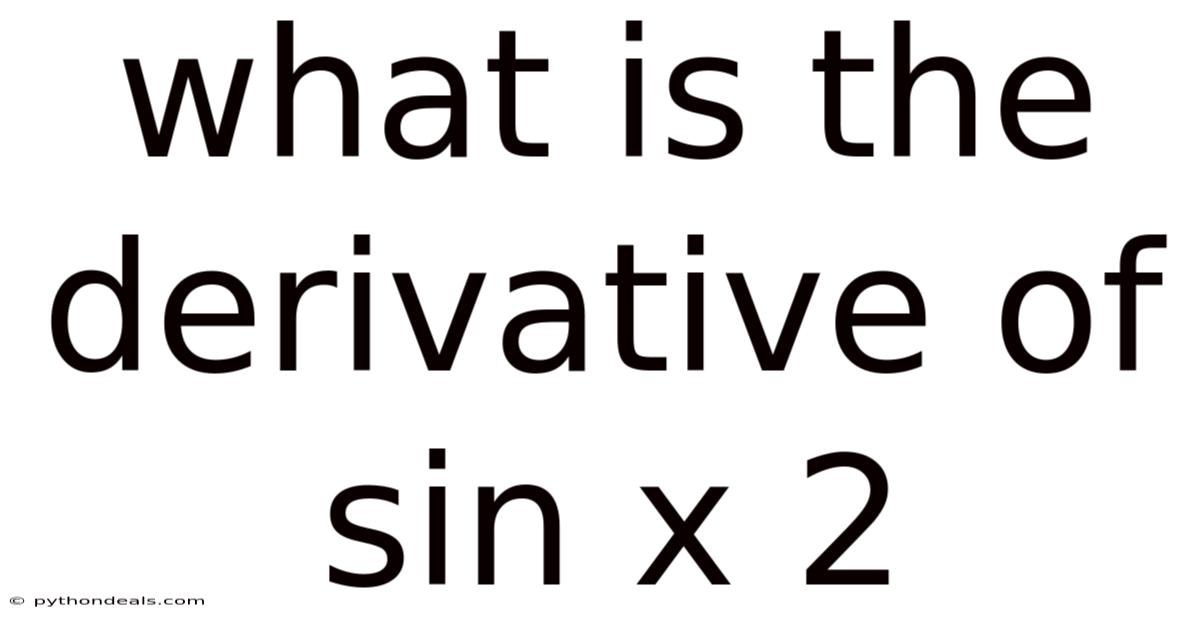
Table of Contents
Let's explore the derivative of sin(x²). It's a topic that combines fundamental concepts of calculus with a bit of algebraic manipulation. Understanding this derivative is crucial for anyone delving into more advanced areas of mathematics, physics, or engineering. It's not just about memorizing a formula; it's about grasping the underlying principles of differentiation.
The derivative of a function represents the instantaneous rate of change of that function. In simpler terms, it tells us how much a function changes as its input changes by an infinitesimally small amount. For sin(x²), we're interested in understanding how the sine of the square of x changes as x itself changes.
Comprehensive Overview
Understanding the Basic Concepts
Before diving into the specific derivative of sin(x²), let's revisit some foundational concepts:
- The Derivative of sin(x): The derivative of sin(x) with respect to x is cos(x). This is a fundamental result that forms the basis for many other derivative calculations involving trigonometric functions.
- The Chain Rule: The chain rule is a crucial concept in calculus that allows us to differentiate composite functions. A composite function is a function that is composed of another function, like our sin(x²). The chain rule states that if we have a function y = f(g(x)), then the derivative of y with respect to x is given by dy/dx = f'(g(x)) * g'(x). In essence, we differentiate the outer function while keeping the inner function unchanged, and then multiply by the derivative of the inner function.
Applying the Chain Rule to sin(x²)
Now, let's apply these concepts to find the derivative of sin(x²). Here, we have a composite function where:
- The outer function is f(u) = sin(u).
- The inner function is g(x) = x².
So, our function is y = f(g(x)) = sin(x²).
To find the derivative dy/dx, we follow these steps:
- Differentiate the outer function: The derivative of f(u) = sin(u) with respect to u is f'(u) = cos(u).
- Differentiate the inner function: The derivative of g(x) = x² with respect to x is g'(x) = 2x.
- Apply the chain rule: According to the chain rule, dy/dx = f'(g(x)) * g'(x). Substituting our results, we get dy/dx = cos(x²) * 2x.
Therefore, the derivative of sin(x²) with respect to x is 2x * cos(x²).
Deeper Dive into the Chain Rule
The chain rule is more than just a formula; it's a fundamental principle that reflects how rates of change propagate through composite functions. Let's break it down further:
Imagine you're adjusting the volume on a sound system. The volume you hear (y) depends on the amplifier setting (u), and the amplifier setting depends on the position of the volume knob (x). If you turn the knob slightly (changing x), it affects the amplifier setting (changing u), which in turn affects the volume (changing y).
The chain rule helps us quantify these relationships. It tells us that the rate at which the volume changes with respect to the knob position (dy/dx) is equal to the rate at which the volume changes with respect to the amplifier setting (dy/du) multiplied by the rate at which the amplifier setting changes with respect to the knob position (du/dx).
This principle applies to many real-world situations, from calculating the speed of a chemical reaction to modeling the population growth of a species. It's a powerful tool for understanding how different variables interact and influence each other.
Visualizing the Derivative
The derivative of sin(x²) is a function that describes the slope of the tangent line to the graph of sin(x²) at any given point. Graphically, it represents how steeply the curve is rising or falling.
To visualize this, imagine drawing a tangent line to the graph of sin(x²) at a particular value of x. The slope of that tangent line is equal to the value of the derivative 2x * cos(x²) at that same value of x.
By plotting the graph of the derivative, we can gain insights into the behavior of the original function. For example, where the derivative is positive, the original function is increasing; where the derivative is negative, the original function is decreasing; and where the derivative is zero, the original function has a local maximum or minimum.
Tren & Perkembangan Terbaru
While the derivative of sin(x²) has been known for centuries, its applications continue to evolve with advances in technology and scientific understanding. Here are some current trends and developments:
- Machine Learning: Derivatives play a crucial role in machine learning algorithms, particularly in the training of neural networks. The chain rule is used extensively to calculate gradients during the backpropagation process, which allows the network to learn from its mistakes and improve its performance.
- Physics Simulations: Derivatives are essential for modeling physical phenomena, such as the motion of objects, the flow of fluids, and the propagation of waves. In complex simulations, numerical methods are often used to approximate derivatives, allowing scientists and engineers to study systems that are too difficult to analyze analytically.
- Financial Modeling: Derivatives are used in financial modeling to assess risk, price options, and develop investment strategies. The derivative of a financial instrument can provide insights into its sensitivity to changes in market conditions, helping investors make informed decisions.
- Symbolic Computation Software: Software packages like Mathematica, Maple, and SymPy can automatically compute derivatives of complex functions, including sin(x²). These tools are invaluable for researchers and engineers who need to perform intricate calculations quickly and accurately.
- Online Educational Resources: Platforms like Khan Academy, Coursera, and edX offer comprehensive courses on calculus, including detailed explanations and interactive exercises on derivatives. These resources make it easier than ever for students to learn and master the fundamental concepts of calculus.
Tips & Expert Advice
Here are some tips and expert advice to master the concept of differentiating sin(x²):
- Master the Basics: Before tackling complex derivatives, make sure you have a solid understanding of the basic differentiation rules, such as the power rule, the product rule, and the quotient rule. Also, familiarize yourself with the derivatives of common functions like sin(x), cos(x), e^x, and ln(x).
- Practice, Practice, Practice: The best way to become proficient at differentiation is to practice solving problems. Start with simple examples and gradually work your way up to more complex ones. There are many online resources and textbooks that offer a wide range of practice problems with solutions.
- Visualize the Concepts: Try to visualize the concepts of derivatives and the chain rule graphically. This can help you develop a deeper understanding of what's actually happening when you differentiate a function. Use graphing software to plot the function and its derivative, and observe how they relate to each other.
- Break Down Complex Functions: When dealing with complex functions, break them down into simpler components. Identify the inner and outer functions, and apply the chain rule step by step. This will make the differentiation process more manageable and less prone to errors.
- Use Symbolic Computation Software: Don't hesitate to use symbolic computation software like Mathematica or Maple to check your work and explore more complex derivatives. These tools can save you time and effort, and they can also help you gain insights into the behavior of functions.
- Understand the Applications: Learning about the applications of derivatives in various fields can make the topic more engaging and relevant. Explore how derivatives are used in physics, engineering, economics, and other areas to see the real-world impact of calculus.
- Seek Help When Needed: If you're struggling with a particular concept or problem, don't be afraid to seek help from your teacher, professor, or classmates. There are also many online forums and communities where you can ask questions and get assistance from experts.
FAQ (Frequently Asked Questions)
Q: What is the derivative of sin(x)?
A: The derivative of sin(x) with respect to x is cos(x).
Q: What is the chain rule?
A: The chain rule is a rule for differentiating composite functions. If y = f(g(x)), then dy/dx = f'(g(x)) * g'(x).
Q: What is the derivative of x²?
A: The derivative of x² with respect to x is 2x.
Q: How do you apply the chain rule to sin(x²)?
A: Let f(u) = sin(u) and g(x) = x². Then, f'(u) = cos(u) and g'(x) = 2x. Applying the chain rule, the derivative of sin(x²) is cos(x²) * 2x, or 2x * cos(x²).
Q: Why is understanding derivatives important?
A: Derivatives are essential for understanding rates of change, optimization problems, and modeling physical phenomena in various fields like physics, engineering, economics, and computer science.
Q: Can symbolic computation software help with derivatives?
A: Yes, software like Mathematica, Maple, and SymPy can automatically compute derivatives of complex functions, saving time and effort.
Conclusion
The derivative of sin(x²) is 2x * cos(x²), a result obtained through the application of the chain rule. This simple yet powerful example illustrates the fundamental principles of calculus and highlights the importance of understanding composite functions. By mastering these concepts, you unlock the ability to analyze and model a wide range of real-world phenomena.
Remember that calculus is not just about memorizing formulas; it's about developing a deep understanding of how things change and interact. So, keep practicing, keep exploring, and keep asking questions. The more you delve into the world of calculus, the more you'll appreciate its beauty and its power.
How do you feel about applying these principles to more complex functions? Are you ready to tackle more challenging derivatives?
Latest Posts
Latest Posts
-
Symmetric With Respect To The Y Axis
Nov 10, 2025
-
Plant Species In The Tropical Rainforest
Nov 10, 2025
-
Can You Graph Points On A Ti 84 Plus
Nov 10, 2025
-
Structures And Molecules Involved In Translation
Nov 10, 2025
-
The Basic Structural And Functional Unit Of The Kidney
Nov 10, 2025
Related Post
Thank you for visiting our website which covers about What Is The Derivative Of Sin X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.