What Is 1 X 1 2
pythondeals
Nov 08, 2025 · 8 min read
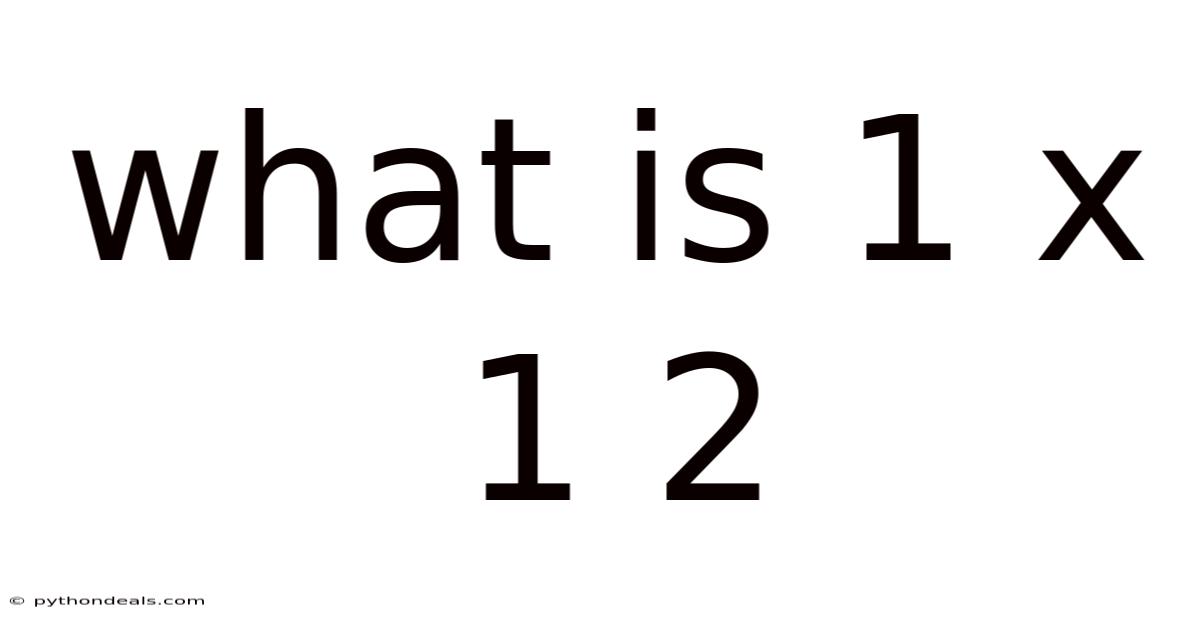
Table of Contents
Let's dive into the seemingly simple, yet surprisingly nuanced question of what 1 x 1/2 is. While the immediate answer might seem obvious, a deeper exploration reveals the underlying principles of multiplication, fractions, and their applications in everyday scenarios. This article will break down the concept step-by-step, offering a comprehensive understanding that goes beyond just arriving at the answer.
Introduction
Mathematics often presents us with problems that appear deceptively straightforward. "What is 1 x 1/2?" falls squarely into this category. At its core, this is a multiplication problem involving a whole number and a fraction. Understanding how these two interact is crucial for grasping more complex mathematical concepts later on. This article will serve as a guide, walking you through the fundamentals, providing real-world examples, and addressing common questions.
Multiplication, at its simplest, is repeated addition. When we multiply 1 by 1/2, we're essentially asking, "What is one group of one-half?" This question can be visualized in various ways, from slicing a pizza to measuring ingredients for a recipe. The answer, of course, is one-half. But the journey to understanding why that's the answer is what we'll explore in detail.
Unpacking Multiplication and Fractions
Before we delve deeper, let's establish a solid foundation by reviewing the basics of multiplication and fractions.
Multiplication: Repeated Addition
Multiplication is a fundamental arithmetic operation representing repeated addition. For example, 3 x 4 means adding the number 4 three times (4 + 4 + 4), which equals 12. Similarly, 5 x 2 means adding the number 2 five times (2 + 2 + 2 + 2 + 2), resulting in 10. This understanding of multiplication as repeated addition is crucial when dealing with fractions.
Fractions: Parts of a Whole
A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the number of parts we have) and 'b' is the denominator (the total number of equal parts the whole is divided into).
- Numerator: Indicates how many parts of the whole you are considering.
- Denominator: Indicates the total number of equal parts the whole is divided into.
For instance, the fraction 1/2 signifies one part out of a total of two equal parts. If you cut a pizza into two equal slices and take one, you have 1/2 of the pizza. Similarly, 3/4 means three parts out of four.
The Calculation: 1 x 1/2
Now, let's directly address the question: What is 1 x 1/2?
As we discussed earlier, multiplication can be thought of as repeated addition. In this case, we're taking one group of 1/2. Mathematically, this can be expressed as:
1 x 1/2 = 1/2
This is because multiplying any number by 1 results in the same number. This is known as the identity property of multiplication. The number 1 is considered the multiplicative identity. Therefore, multiplying 1/2 by 1 simply gives us 1/2.
Visual Representation
Imagine you have a single cookie. You want to give away half of that cookie. This means you are giving away 1/2 of one cookie. Therefore, 1 x 1/2 = 1/2.
Another way to visualize this is with a number line. If you start at 0 and move 1/2 of a unit in a single step, you end up at 1/2. This represents one step of size 1/2, or 1 x 1/2.
Real-World Applications
Understanding 1 x 1/2 might seem elementary, but it forms the basis for many practical applications in everyday life.
Cooking and Baking:
Recipes often involve fractions. For example, a recipe might call for 1/2 cup of sugar. If you are making only one batch of the recipe, you need 1 x 1/2 = 1/2 cup of sugar. This concept extends to measuring various ingredients, helping you scale recipes accurately.
Construction and Measurement:
In construction, measurements frequently involve fractions. A carpenter might need to cut a piece of wood that is 1/2 inch thick. If they only need one such piece, they need 1 x 1/2 = 1/2 inch of wood.
Time Management:
Consider time management. If you allocate 1/2 hour for a task and perform it only once, you are spending 1 x 1/2 = 1/2 hour on that task.
Financial Calculations:
Even in finance, this basic understanding is useful. If you own 1 share of a company and that share pays a dividend of $0.50 (which can be represented as 1/2 dollar), your dividend income from that one share is 1 x $0.50 = $0.50.
Example Problems:
-
Problem: You have one pizza, and you eat half of it. How much pizza did you eat?
- Solution: 1 x 1/2 = 1/2 of the pizza.
-
Problem: You are running a 1-mile race. You run half a mile. How much of the race have you completed?
- Solution: 1 x 1/2 = 1/2 of the race.
-
Problem: A piece of cloth is 1 meter long. You cut off half of it. How long is the piece you cut off?
- Solution: 1 x 1/2 = 1/2 meter.
Exploring More Complex Scenarios
While 1 x 1/2 is straightforward, it's a stepping stone to understanding more complex multiplication involving fractions. Let's briefly touch upon some related scenarios.
Multiplying Fractions by Fractions:
To multiply fractions, you multiply the numerators together and the denominators together. For example, 1/2 x 1/3 = (1 x 1) / (2 x 3) = 1/6.
Multiplying Whole Numbers by Mixed Numbers:
A mixed number consists of a whole number and a fraction (e.g., 2 1/2). To multiply a whole number by a mixed number, you can convert the mixed number into an improper fraction first. For example, 2 1/2 can be converted to 5/2. Then you can multiply. 3 x 2 1/2 = 3 x 5/2 = 15/2 = 7 1/2.
Dividing by Fractions:
Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 1/2 is 2/1 or simply 2. So, dividing by 1/2 is the same as multiplying by 2.
Common Misconceptions and Clarifications
Even with a seemingly simple calculation like 1 x 1/2, some misconceptions can arise.
Misconception 1: Multiplying Always Makes the Result Bigger
This is not always true, especially when dealing with fractions less than 1. Multiplying by a fraction less than 1 actually makes the result smaller. For example, 10 x 1/2 = 5, which is smaller than 10.
Misconception 2: Fractions are Difficult to Understand
Fractions can seem daunting, but they are simply a way to represent parts of a whole. Visual aids and real-world examples can greatly aid in understanding fractions.
Clarification: 1 x 1/2 means taking one group of one-half. It doesn't mean dividing 1 by 2. While the numerical result is the same, the underlying concept is different.
The Mathematical Significance
Understanding 1 x 1/2 isn't just about getting the correct answer; it's about grasping the foundational principles that underpin more advanced mathematics. This simple calculation demonstrates the identity property of multiplication, the nature of fractions, and the relationship between multiplication and division.
This understanding is crucial for learning algebra, calculus, and other advanced mathematical topics. These concepts build upon the basic understanding of numbers and operations.
Tips for Teaching and Learning
Here are some helpful tips for teaching and learning this concept:
- Use Visual Aids: Diagrams, number lines, and physical objects can make the concept more concrete and easier to understand.
- Real-World Examples: Relate the concept to everyday situations like cooking, sharing, and measuring.
- Hands-on Activities: Engage students with hands-on activities like cutting paper or using fraction manipulatives.
- Practice Problems: Provide plenty of practice problems to reinforce the concept and build confidence.
- Address Misconceptions: Be aware of common misconceptions and address them directly.
Tren & Perkembangan Terbaru
While the core concept of 1 x 1/2 remains constant, its application and teaching methods continue to evolve with advancements in technology and pedagogy. Educational apps and interactive simulations are increasingly used to make learning more engaging and accessible. Online resources provide a wealth of information and practice problems.
Furthermore, there is a growing emphasis on conceptual understanding rather than rote memorization. Educators are focusing on helping students understand why the math works, not just how to do it.
Conclusion
The question "What is 1 x 1/2?" may appear simple, but it opens the door to a deeper understanding of fundamental mathematical principles. It illustrates the essence of multiplication, the nature of fractions, and their relevance in everyday life. By grasping this basic concept, we lay a solid foundation for exploring more complex mathematical ideas. So, the next time you encounter a seemingly simple math problem, remember that there's often more to it than meets the eye. Embrace the opportunity to delve deeper, explore the underlying principles, and expand your understanding of the mathematical world.
How do you use fractions in your daily life? Have you ever encountered any surprising applications of basic math? I'd love to hear your thoughts and experiences!
Latest Posts
Latest Posts
-
T Test One Tailed Vs Two Tailed
Nov 08, 2025
-
Example Of Main Idea In A Paragraph
Nov 08, 2025
-
Which Of The Following Organisms Are Unicellular
Nov 08, 2025
-
How Do You Calculate The Square Footage Of A Triangle
Nov 08, 2025
-
What Is Absolute Value Of 7
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.