What Is Absolute Value Of -7
pythondeals
Nov 08, 2025 · 11 min read
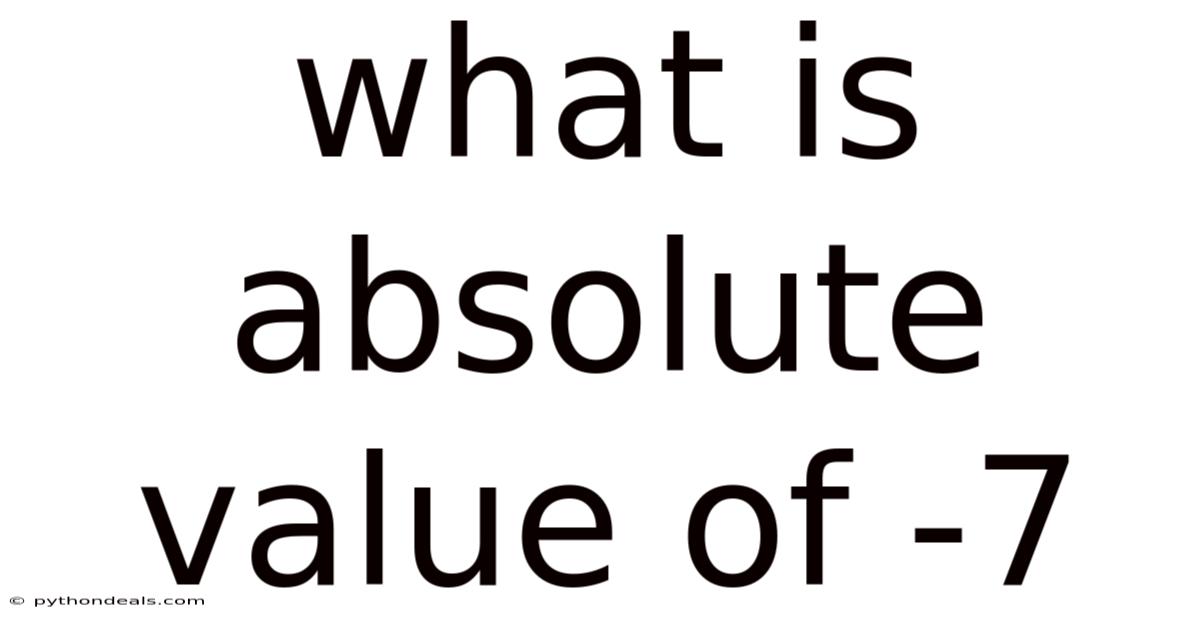
Table of Contents
The concept of absolute value might seem simple on the surface, but it's a cornerstone of mathematical understanding and has practical applications in numerous fields. When someone asks, "What is the absolute value of -7?" the immediate answer is 7. But diving deeper into why that's the case reveals a world of fundamental mathematical principles. Let's explore this concept, from its definition to its uses, and even tackle some common misconceptions along the way.
Absolute value is more than just dropping the negative sign. It represents the distance of a number from zero on the number line, regardless of direction. This might seem like a subtle distinction, but it's crucial for understanding its applications in more complex mathematical problems.
Understanding Absolute Value
The absolute value of a number, denoted by |x|, is its distance from zero on the number line. Because distance is always non-negative, the absolute value of any number will always be either positive or zero. Mathematically, we can define it as follows:
|x| = x, if x ≥ 0 |x| = -x, if x < 0
This definition tells us that if the number is already positive or zero, its absolute value is simply the number itself. However, if the number is negative, we take its opposite (which is positive) to find its absolute value.
Historical Context
The concept of absolute value has evolved over time, becoming more formalized as mathematics advanced. While the idea of magnitude or size has always been intuitive, the formal notation and application of absolute value as a distinct function arose in the 19th century. Mathematicians like Karl Weierstrass contributed significantly to its rigorous definition, helping to solidify its place in mathematical analysis.
The Absolute Value of -7: A Detailed Explanation
So, what is the absolute value of -7? Let's break it down:
- Identify the number: We are dealing with the number -7.
- Apply the definition: Since -7 is less than 0, we use the second part of the absolute value definition: |-7| = -(-7).
- Simplify: -(-7) equals 7.
Therefore, the absolute value of -7 is 7. This means that -7 is 7 units away from zero on the number line.
Visualizing on the Number Line
Imagine a number line stretching infinitely in both directions. Zero is at the center. The number -7 is located 7 units to the left of zero. The absolute value of -7 is simply the distance from -7 to zero, which is 7 units. The same logic applies to the number 7, which is located 7 units to the right of zero. Its absolute value is also 7.
Why is Absolute Value Important?
Absolute value is not just an abstract mathematical concept. It is essential in various fields, including:
- Physics: When dealing with vectors, speed (which is the magnitude of velocity) is often calculated using absolute value. The direction doesn't matter; only the magnitude does.
- Engineering: In error analysis, absolute value is used to determine the magnitude of the error, regardless of whether it's an overestimation or underestimation.
- Computer Science: Absolute value is used in algorithms for distance calculations, such as finding the distance between two points on a screen.
- Economics: When analyzing deviations from a target value, absolute value can be used to measure the size of the deviation, irrespective of whether it's above or below the target.
- Everyday Life: Consider scenarios like measuring temperature differences. The difference between 20°C and 25°C is the same in magnitude as the difference between 25°C and 20°C, even though the direction (increase or decrease) is different. Absolute value helps quantify this magnitude.
Mathematical Properties of Absolute Value
Understanding the properties of absolute value is crucial for solving equations and inequalities involving it. Here are some key properties:
- Non-negativity: |a| ≥ 0 for all real numbers 'a'. This is because distance cannot be negative.
- Symmetry: |-a| = |a| for all real numbers 'a'. A number and its negative are equidistant from zero.
- Product: |ab| = |a| |b| for all real numbers 'a' and 'b'. The absolute value of a product is the product of the absolute values.
- Quotient: |a/b| = |a| / |b| for all real numbers 'a' and 'b', where b ≠ 0. The absolute value of a quotient is the quotient of the absolute values.
- Triangle Inequality: |a + b| ≤ |a| + |b| for all real numbers 'a' and 'b'. This property is widely used in various mathematical proofs and has significant implications in fields like analysis and topology.
Solving Equations and Inequalities with Absolute Value
Absolute value can make solving equations and inequalities a bit trickier. This is because the absolute value function effectively splits the problem into two cases: the case where the expression inside the absolute value is positive or zero, and the case where it's negative.
Solving Equations
Consider the equation |x| = 5. This equation has two solutions:
- Case 1: x ≥ 0: In this case, |x| = x, so x = 5.
- Case 2: x < 0: In this case, |x| = -x, so -x = 5, which means x = -5.
Therefore, the solutions to the equation |x| = 5 are x = 5 and x = -5.
Solving Inequalities
Consider the inequality |x| < 3. This inequality means that the distance of 'x' from zero must be less than 3. This leads to the following:
- -3 < x < 3
This means that 'x' must be greater than -3 and less than 3. The solution set is the open interval (-3, 3).
Now consider the inequality |x| > 2. This inequality means that the distance of 'x' from zero must be greater than 2. This leads to the following two cases:
- Case 1: x > 2
- Case 2: x < -2
The solution set is the union of the intervals (-∞, -2) and (2, ∞).
General Strategies
When solving equations or inequalities involving absolute value, it's crucial to:
- Isolate the absolute value expression: Before splitting into cases, isolate the absolute value term on one side of the equation or inequality.
- Split into cases: Consider the two possible cases: the expression inside the absolute value is non-negative, and the expression inside the absolute value is negative.
- Solve each case: Solve the resulting equation or inequality for each case.
- Check solutions: It's crucial to check the solutions obtained in each case to ensure they satisfy the original equation or inequality. This is particularly important when dealing with inequalities, as extraneous solutions can arise.
Common Misconceptions About Absolute Value
Despite its seemingly straightforward definition, absolute value is often misunderstood. Here are some common misconceptions:
- Absolute value always makes a number positive: This is true for negative numbers, but the absolute value of a positive number is the number itself, and the absolute value of zero is zero. So, absolute value doesn't always make a number positive; it ensures the result is non-negative.
- Absolute value is the same as removing the negative sign: While this works for negative numbers, it's important to understand the underlying concept of distance. Simply removing the negative sign doesn't explain why the absolute value is what it is.
- |a + b| = |a| + |b|: This is not generally true. This equality holds only when 'a' and 'b' have the same sign (or at least one of them is zero). The correct relationship is given by the triangle inequality: |a + b| ≤ |a| + |b|.
- Absolute value is only used in pure mathematics: As mentioned earlier, absolute value has numerous applications in physics, engineering, computer science, economics, and even everyday life.
Absolute Value in Real-World Applications: A Deeper Dive
Let's explore some real-world applications of absolute value in more detail:
1. Physics: Calculating Speed
In physics, velocity is a vector quantity, meaning it has both magnitude (speed) and direction. Speed, on the other hand, is a scalar quantity and only refers to the magnitude of the velocity. When calculating speed, we often use absolute value.
For example, if an object has a velocity of -10 m/s (moving to the left), its speed is |-10| = 10 m/s. The negative sign indicates the direction, but the absolute value gives us the magnitude of the motion.
2. Engineering: Error Analysis
In engineering, it's crucial to quantify errors in measurements and calculations. Absolute value is used to determine the magnitude of the error, regardless of whether the measured value is higher or lower than the true value.
For example, if the true length of a beam is 5 meters and a measurement gives a length of 4.95 meters, the absolute error is |5 - 4.95| = |0.05| = 0.05 meters. Similarly, if the measurement gives a length of 5.05 meters, the absolute error is |5 - 5.05| = |-0.05| = 0.05 meters. In both cases, the absolute error tells us the magnitude of the deviation from the true value.
3. Computer Science: Distance Calculations
In computer graphics and game development, calculating the distance between two points is a fundamental operation. If two points are on a single axis (e.g., the x-axis), the distance between them can be found using absolute value.
For example, if point A has an x-coordinate of 2 and point B has an x-coordinate of 7, the distance between them is |7 - 2| = |5| = 5 units. This calculation works regardless of which point is considered the "starting" point. The distance is also |2-7| = |-5| = 5.
4. Economics: Measuring Deviations
In economics, absolute value is used to measure deviations from a target value or benchmark. This is particularly useful when analyzing economic indicators like inflation rates or unemployment rates.
For example, if the target inflation rate is 2% and the actual inflation rate is 2.5%, the deviation from the target is |2 - 2.5| = |-0.5| = 0.5 percentage points. This tells us how far the actual inflation rate is from the target, regardless of whether it's above or below the target.
5. Signal Processing
In signal processing, absolute value is used in rectification, a process that converts an alternating current (AC) signal to a direct current (DC) signal. A full-wave rectifier uses absolute value to flip the negative portions of the AC signal to positive, resulting in a pulsating DC signal.
Trends and Recent Developments
While the fundamental concept of absolute value remains unchanged, its application in advanced mathematical and computational fields continues to evolve. Here are some recent trends and developments:
- Machine Learning: Absolute value is increasingly used in machine learning algorithms, particularly in loss functions like the L1 loss (Mean Absolute Error). L1 loss is less sensitive to outliers compared to the L2 loss (Mean Squared Error), making it suitable for datasets with noisy data.
- Optimization: Absolute value functions can be challenging to optimize due to their non-differentiability at zero. Researchers are developing new optimization algorithms specifically designed to handle absolute value functions and other non-smooth functions.
- Quantum Computing: While still in its early stages, quantum computing utilizes concepts related to absolute value in defining quantum states and measuring probabilities. The absolute square of a complex number represents the probability of finding a quantum system in a particular state.
Expert Advice and Tips
- Master the Definition: A solid understanding of the definition of absolute value is crucial for solving problems correctly. Don't just memorize the "remove the negative sign" rule; understand the concept of distance from zero.
- Practice Solving Equations and Inequalities: Solving equations and inequalities involving absolute value requires careful attention to detail and a systematic approach. Practice a variety of problems to build your skills.
- Visualize on the Number Line: When dealing with absolute value, visualizing the numbers on the number line can be helpful for understanding the concept and solving problems.
- Be Aware of Common Mistakes: Avoid common misconceptions about absolute value. Remember that |a + b| is not always equal to |a| + |b|, and that absolute value doesn't always make a number positive.
- Use Absolute Value in Real-World Applications: Applying absolute value to real-world scenarios can help you appreciate its importance and relevance.
FAQ (Frequently Asked Questions)
-
Q: What is the absolute value of 0?
- A: The absolute value of 0 is 0.
-
Q: Can the absolute value of a number be negative?
- A: No, the absolute value of a number is always non-negative (positive or zero).
-
Q: How do you solve an equation with absolute value?
- A: Isolate the absolute value expression, split the equation into two cases (positive and negative), solve each case, and check your solutions.
-
Q: What is the triangle inequality?
- A: The triangle inequality states that |a + b| ≤ |a| + |b| for all real numbers 'a' and 'b'.
-
Q: What is the difference between absolute error and relative error?
- A: Absolute error is the magnitude of the difference between a measured value and the true value. Relative error is the absolute error divided by the true value, often expressed as a percentage.
Conclusion
Understanding the absolute value of -7, which is 7, is more than just knowing a simple fact. It's about grasping the fundamental concept of distance from zero and its broader implications in mathematics and beyond. From physics to computer science, absolute value plays a crucial role in quantifying magnitude, analyzing errors, and solving a wide range of problems. By mastering the definition, properties, and applications of absolute value, you'll be well-equipped to tackle more advanced mathematical concepts and real-world challenges.
What other mathematical concepts do you find challenging, and how can a deeper understanding of fundamental principles help? Are there any specific applications of absolute value you find particularly interesting?
Latest Posts
Latest Posts
-
Does A Virus Have A Nucleus
Nov 08, 2025
-
How To Find The Range Of A Group Of Numbers
Nov 08, 2025
-
How Do You Make A Parallelogram
Nov 08, 2025
-
Unlike The Legislative And Executive Branches Judges And Courts
Nov 08, 2025
-
What Is The Hereditary Material Found In All Cells
Nov 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Absolute Value Of -7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.