Integral Of 1 Sqrt X 2 4
pythondeals
Nov 26, 2025 · 8 min read
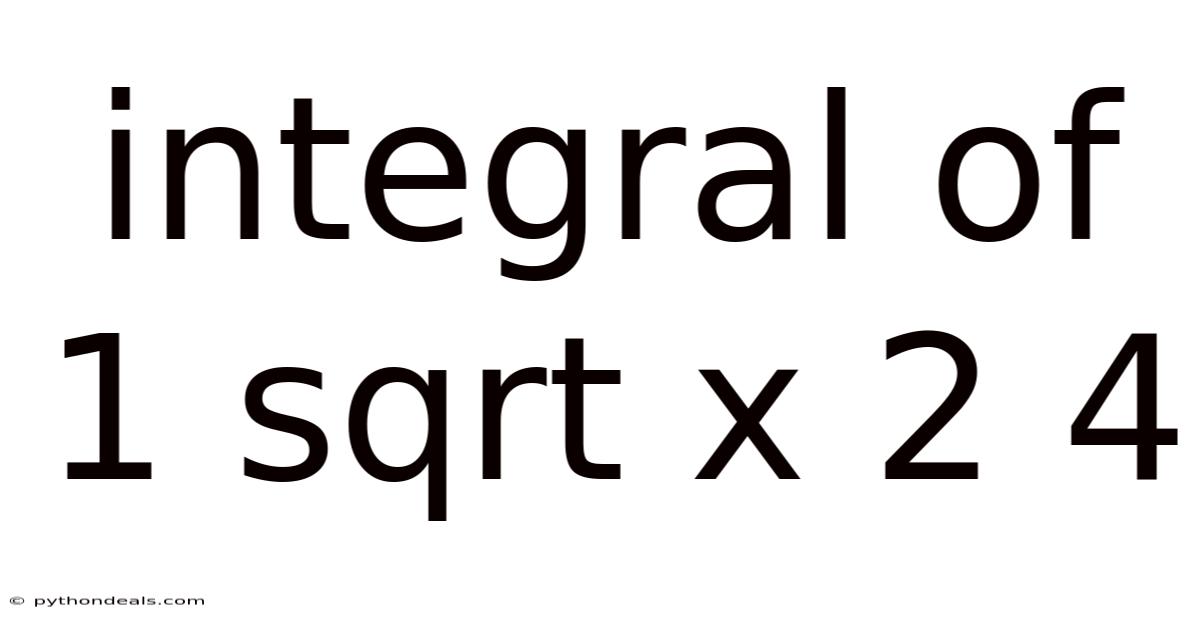
Table of Contents
Here's a detailed article addressing the integral of 1/√(x^2 + 4), aiming for clarity, depth, and practical understanding.
Navigating the Integral of 1/√(x² + 4): A Comprehensive Guide
The world of calculus often presents us with intriguing challenges, and the integral of 1/√(x² + 4) is a classic example. It’s not immediately obvious how to approach this problem, but with the right techniques and a bit of trigonometric substitution, we can unravel it. This article will delve into the methods needed to solve this integral, providing you with a step-by-step guide, insightful explanations, and practical tips.
This integral falls under the category of integrals involving square roots of quadratic expressions. Specifically, it features the form √(x² + a²), where 'a' in our case is 2. Recognizing this form is crucial because it immediately suggests the use of a trigonometric substitution. The most appropriate substitution here is x = a * tan(θ), which simplifies the square root and allows us to transform the integral into a more manageable form.
Setting the Stage: Understanding the Integral
The integral we aim to solve is:
∫ 1/√(x² + 4) dx
Before diving into the solution, it's beneficial to understand why this integral is significant. Integrals of this nature frequently appear in physics, engineering, and various branches of applied mathematics. They often arise when dealing with problems involving distances, areas, or volumes in curved spaces, particularly in scenarios involving hyperbolic geometry. For instance, calculating the arc length of a hyperbola can lead to integrals of this form. Furthermore, understanding how to solve this integral equips you with a valuable tool for tackling more complex integrals you might encounter in advanced calculus courses or real-world applications.
The Key: Trigonometric Substitution
The cornerstone of solving this integral is the application of trigonometric substitution. Specifically, we use the substitution x = 2 * tan(θ). This substitution is strategically chosen because it allows us to simplify the expression under the square root.
Here’s how it works:
-
Substitution: Let x = 2 * tan(θ). This implies that dx = 2 * sec²(θ) dθ.
-
Simplifying the Square Root: Substitute x into the square root expression:
√(x² + 4) = √((2 * tan(θ))² + 4) = √(4 * tan²(θ) + 4) = √(4 * (tan²(θ) + 1))
Since tan²(θ) + 1 = sec²(θ), we have:
√(4 * sec²(θ)) = 2 * sec(θ)
-
Rewriting the Integral: Now, substitute x and dx in the original integral:
∫ 1/√(x² + 4) dx = ∫ (1 / (2 * sec(θ))) * (2 * sec²(θ) dθ) = ∫ sec(θ) dθ
Solving the Transformed Integral: ∫ sec(θ) dθ
The integral of sec(θ) is a well-known result in calculus, but it's worth revisiting how it is derived. The standard method involves a clever trick: multiplying the integrand by (sec(θ) + tan(θ)) / (sec(θ) + tan(θ)).
Here’s the derivation:
∫ sec(θ) dθ = ∫ sec(θ) * (sec(θ) + tan(θ)) / (sec(θ) + tan(θ)) dθ
= ∫ (sec²(θ) + sec(θ) * tan(θ)) / (sec(θ) + tan(θ)) dθ
Now, observe that the numerator is the derivative of the denominator. Specifically, the derivative of sec(θ) + tan(θ) is sec(θ) * tan(θ) + sec²(θ). This allows us to perform a simple u-substitution.
Let u = sec(θ) + tan(θ). Then du = (sec(θ) * tan(θ) + sec²(θ)) dθ.
The integral becomes:
∫ 1/u du = ln|u| + C = ln|sec(θ) + tan(θ)| + C
Therefore, ∫ sec(θ) dθ = ln|sec(θ) + tan(θ)| + C
Back to the Original Variable: Reversing the Substitution
Now that we have the result in terms of θ, we need to express it in terms of the original variable, x. Recall that we made the substitution x = 2 * tan(θ), which means tan(θ) = x/2.
To find sec(θ), we can use the identity sec²(θ) = 1 + tan²(θ).
sec²(θ) = 1 + (x/2)² = 1 + x²/4 = (4 + x²) / 4
Taking the square root of both sides:
sec(θ) = √(4 + x²) / 2
Now, substitute tan(θ) = x/2 and sec(θ) = √(4 + x²) / 2 into the expression ln|sec(θ) + tan(θ)| + C:
ln|sec(θ) + tan(θ)| + C = ln|√(4 + x²) / 2 + x/2| + C
= ln|(√(x² + 4) + x) / 2| + C
Using the property of logarithms, ln(a/b) = ln(a) - ln(b):
ln|(√(x² + 4) + x) / 2| + C = ln|√(x² + 4) + x| - ln(2) + C
Since ln(2) is a constant, we can absorb it into the constant of integration:
ln|√(x² + 4) + x| - ln(2) + C = ln|√(x² + 4) + x| + C'
Therefore, the final result is:
∫ 1/√(x² + 4) dx = ln|x + √(x² + 4)| + C
Alternative Approach: Hyperbolic Functions
Another elegant way to solve this integral involves recognizing that the integral is directly related to the inverse hyperbolic sine function, denoted as sinh⁻¹(x). Let's explore this connection:
Recall that sinh(y) = (e^y - e^(-y)) / 2
The inverse hyperbolic sine, sinh⁻¹(x), is defined such that if x = sinh(y), then y = sinh⁻¹(x).
The derivative of sinh⁻¹(x) is given by:
d/dx [sinh⁻¹(x)] = 1 / √(x² + 1)
Now, let's consider our integral: ∫ 1/√(x² + 4) dx
We can rewrite this as:
∫ 1/√(x² + 4) dx = ∫ 1 / (2 * √((x/2)² + 1)) dx
Now, perform a simple substitution: let u = x/2, so dx = 2 du
The integral becomes:
∫ 1 / (2 * √(u² + 1)) * 2 du = ∫ 1 / √(u² + 1) du
This is now in the form of the derivative of sinh⁻¹(u):
∫ 1 / √(u² + 1) du = sinh⁻¹(u) + C
Now substitute back u = x/2:
sinh⁻¹(x/2) + C
Thus,
∫ 1/√(x² + 4) dx = sinh⁻¹(x/2) + C
This result is equivalent to the logarithmic form we derived earlier. The relationship between the inverse hyperbolic sine and the natural logarithm is given by:
sinh⁻¹(x) = ln(x + √(x² + 1))
Therefore,
sinh⁻¹(x/2) = ln(x/2 + √((x/2)² + 1)) = ln((x + √(x² + 4)) / 2)
As we saw earlier, the division by 2 inside the logarithm simply adds a constant, which can be absorbed into the constant of integration, giving us:
ln(x + √(x² + 4)) + C
Comprehensive Overview: Key Concepts and Techniques
- Trigonometric Substitution: This technique is crucial for integrals involving expressions of the form √(a² - x²), √(x² + a²), or √(x² - a²). The substitutions are x = a * sin(θ), x = a * tan(θ), and x = a * sec(θ), respectively.
- Hyperbolic Functions: Recognizing the relationship between integrals and inverse hyperbolic functions can provide an elegant and efficient solution.
- Algebraic Manipulation: Simplifying the integrand through algebraic manipulation is often necessary before applying more advanced techniques.
- Constant of Integration: Always remember to add the constant of integration, C, to the final result of an indefinite integral.
Tren & Perkembangan Terbaru
While the core techniques for solving integrals like ∫ 1/√(x² + 4) dx have been established for centuries, modern computational tools and software packages have significantly streamlined the process. Software like Mathematica, Maple, and Wolfram Alpha can quickly compute these integrals, but understanding the underlying methods remains crucial for problem-solving and gaining deeper insights. In educational settings, there's a growing emphasis on combining these computational tools with traditional analytical methods to provide students with a more comprehensive understanding of calculus.
Tips & Expert Advice
- Master Basic Trigonometric Identities: A strong foundation in trigonometric identities is essential for successful trigonometric substitution. Know your Pythagorean identities, double-angle formulas, and reciprocal identities.
- Practice, Practice, Practice: The more integrals you solve, the better you'll become at recognizing patterns and choosing the appropriate techniques.
- Check Your Work: Always differentiate your final result to verify that you obtain the original integrand. This helps catch errors in your integration process.
- Use Technology Wisely: While computational tools can be helpful, don't rely on them blindly. Use them to check your work and explore different approaches, but always strive to understand the underlying principles.
- Visualize the Problem: Whenever possible, try to visualize the function you're integrating. This can provide valuable insights and help you anticipate the result. For instance, you might recognize symmetries or asymptotic behaviors.
FAQ (Frequently Asked Questions)
- Q: Why do we use trigonometric substitution?
- A: Trigonometric substitution helps simplify integrals involving square roots of quadratic expressions by transforming them into more manageable trigonometric integrals.
- Q: Can I use a different trigonometric substitution?
- A: While x = 2 * tan(θ) is the most common and straightforward substitution for ∫ 1/√(x² + 4) dx, other substitutions might be possible but less efficient.
- Q: How do I know which trigonometric substitution to use?
- A: The choice of substitution depends on the form of the expression under the square root. For √(a² - x²), use x = a * sin(θ); for √(x² + a²), use x = a * tan(θ); for √(x² - a²), use x = a * sec(θ).
- Q: What is the significance of the constant of integration?
- A: The constant of integration, C, represents the family of functions that have the same derivative. Since the derivative of a constant is zero, any constant can be added to the antiderivative without changing its derivative.
- Q: Are the logarithmic and hyperbolic forms of the solution equivalent?
- A: Yes, the logarithmic form ln|x + √(x² + 4)| + C and the hyperbolic form sinh⁻¹(x/2) + C are equivalent. They differ by a constant, which is absorbed into the constant of integration.
Conclusion
The integral of 1/√(x² + 4) provides a compelling illustration of the power and elegance of calculus techniques. By mastering trigonometric substitution and understanding the relationship with hyperbolic functions, you can confidently tackle similar integrals and deepen your understanding of calculus. Remember to practice regularly, check your work, and use technology as a tool to enhance your learning.
How do you feel about using trigonometric substitution to solve complex integrals? Are you inspired to tackle more challenging integration problems?
Latest Posts
Latest Posts
-
What Is A Loose Monetary Policy
Nov 26, 2025
-
Integral Of 1 Sqrt X 2 4
Nov 26, 2025
-
What Is Quantum Of Light Called
Nov 26, 2025
-
The Correct Progression Of Steps Of The Nursing Process Is
Nov 26, 2025
-
How To Find Height Of A Triangle With Base
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 Sqrt X 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.