Which Is Bigger 1/4 1/8 Or 3/16
pythondeals
Nov 19, 2025 · 9 min read
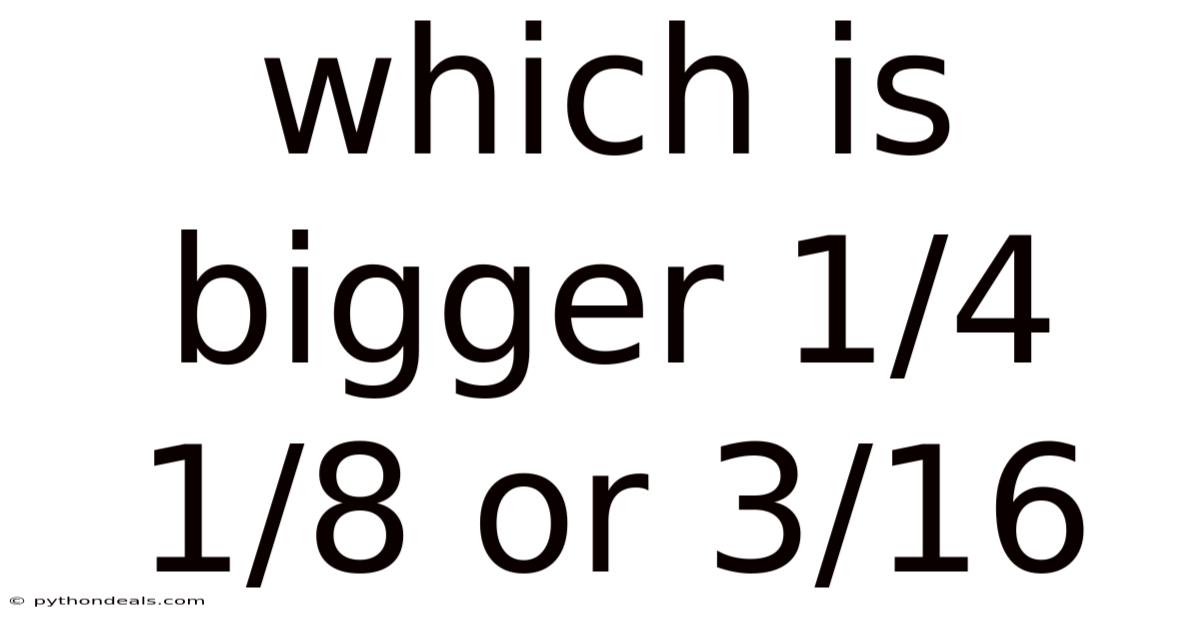
Table of Contents
Let's dive into the world of fractions! It might seem straightforward at first glance, but comparing fractions like 1/4, 1/8, and 3/16 requires a bit of understanding about how fractions work. In this article, we'll explore several methods to determine which of these fractions is the largest. Whether you’re a student brushing up on your math skills or just curious, this guide will provide a clear and comprehensive explanation. So, which is bigger, 1/4, 1/8, or 3/16? Keep reading to find out!
Understanding Fractions: A Quick Refresher
Before we jump into comparing the fractions, let's quickly review what a fraction represents. A fraction is a way to represent a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
For example, in the fraction 1/4:
- 1 is the numerator, indicating we have one part.
- 4 is the denominator, indicating the whole is divided into four equal parts.
Fractions can represent:
- Parts of a whole: As mentioned above.
- Ratios: Comparing two quantities.
- Division: The fraction a/b is the same as a ÷ b.
Understanding these basics is crucial before we start comparing the fractions 1/4, 1/8, and 3/16.
Method 1: Visual Comparison Using Diagrams
One of the most intuitive ways to compare fractions is through visual representation. This method is especially helpful for those who are new to fractions or find it easier to understand concepts visually.
Drawing the Fractions
-
Draw Identical Rectangles: Start by drawing three identical rectangles. These rectangles represent the 'whole' that we are dividing into fractions.
-
Divide the Rectangles:
- 1/4: Divide the first rectangle into four equal parts. Shade one of these parts to represent 1/4.
- 1/8: Divide the second rectangle into eight equal parts. Shade one of these parts to represent 1/8.
- 3/16: Divide the third rectangle into sixteen equal parts. Shade three of these parts to represent 3/16.
Comparing the Shaded Areas
Now that you have visually represented each fraction, compare the shaded areas of the rectangles. By looking at the diagrams, you can observe which shaded area is the largest.
Conclusion from Visual Comparison
From the visual comparison, it's clear that:
- The shaded area representing 1/4 is larger than the shaded area representing 1/8.
- The shaded area representing 1/4 is also larger than the shaded area representing 3/16.
- The shaded area representing 3/16 is larger than the shaded area representing 1/8.
Therefore, based on the visual comparison, we can conclude that 1/4 is the largest fraction among the three.
Method 2: Finding a Common Denominator
Another effective method to compare fractions is by finding a common denominator. This involves converting the fractions to equivalent fractions that all have the same denominator. Once they have the same denominator, it's easy to compare the numerators to determine which fraction is the largest.
What is a Common Denominator?
A common denominator is a number that is a multiple of all the denominators in the set of fractions you are comparing. The least common denominator (LCD) is the smallest number that fits this criterion, making calculations simpler.
Finding the Least Common Denominator (LCD)
For the fractions 1/4, 1/8, and 3/16, we need to find the LCD of 4, 8, and 16.
- Multiples of 4: 4, 8, 12, 16, 20, ...
- Multiples of 8: 8, 16, 24, 32, ...
- Multiples of 16: 16, 32, 48, ...
The smallest number that appears in all three lists is 16. Therefore, the LCD of 4, 8, and 16 is 16.
Converting the Fractions to Equivalent Fractions
Now that we have the LCD, we need to convert each fraction to an equivalent fraction with a denominator of 16.
-
1/4:
- To convert 1/4 to a fraction with a denominator of 16, we need to multiply both the numerator and the denominator by the same number so that the denominator becomes 16.
- 4 × ? = 16
- 4 × 4 = 16
- So, we multiply both the numerator and the denominator of 1/4 by 4:
- (1 × 4) / (4 × 4) = 4/16
-
1/8:
- To convert 1/8 to a fraction with a denominator of 16, we need to multiply both the numerator and the denominator by the same number so that the denominator becomes 16.
- 8 × ? = 16
- 8 × 2 = 16
- So, we multiply both the numerator and the denominator of 1/8 by 2:
- (1 × 2) / (8 × 2) = 2/16
-
3/16:
- The fraction 3/16 already has a denominator of 16, so no conversion is needed.
Comparing the Equivalent Fractions
Now we have the following equivalent fractions:
- 1/4 = 4/16
- 1/8 = 2/16
- 3/16 = 3/16
Since all the fractions have the same denominator, we can now compare the numerators. The fraction with the largest numerator is the largest fraction. Comparing the numerators:
- 4 > 3
- 4 > 2
- 3 > 2
Therefore, 4/16 is the largest fraction, which means 1/4 is the largest among the original fractions.
Conclusion from Common Denominator Method
Using the common denominator method, we again find that 1/4 is the largest fraction.
Method 3: Converting Fractions to Decimals
Another way to compare fractions is by converting them to decimal form. This method is particularly useful when dealing with fractions that are difficult to compare directly or when you have access to a calculator.
Converting Fractions to Decimals
To convert a fraction to a decimal, you simply divide the numerator by the denominator.
-
1/4:
- 1 ÷ 4 = 0.25
-
1/8:
- 1 ÷ 8 = 0.125
-
3/16:
- 3 ÷ 16 = 0.1875
Comparing the Decimal Values
Now that we have the decimal equivalents of the fractions, we can easily compare them.
- 1/4 = 0.25
- 1/8 = 0.125
- 3/16 = 0.1875
Comparing the decimal values:
- 0.25 > 0.1875
- 0.25 > 0.125
- 0.1875 > 0.125
From the comparison, it's clear that 0.25 is the largest decimal value.
Conclusion from Decimal Conversion
Based on the decimal conversion method, we confirm that 1/4 (0.25) is the largest fraction among 1/4, 1/8, and 3/16.
Method 4: Cross-Multiplication
Cross-multiplication is a quick method to compare two fractions at a time. It involves multiplying the numerator of one fraction by the denominator of the other fraction and vice versa. The fraction with the larger product is the larger fraction.
Comparing 1/4 and 1/8
-
Cross-Multiply:
- 1/4 vs. 1/8
- (1 × 8) vs. (1 × 4)
- 8 vs. 4
-
Compare the Products:
- Since 8 is greater than 4, 1/4 is greater than 1/8.
Comparing 1/4 and 3/16
-
Cross-Multiply:
- 1/4 vs. 3/16
- (1 × 16) vs. (3 × 4)
- 16 vs. 12
-
Compare the Products:
- Since 16 is greater than 12, 1/4 is greater than 3/16.
Comparing 1/8 and 3/16
-
Cross-Multiply:
- 1/8 vs. 3/16
- (1 × 16) vs. (3 × 8)
- 16 vs. 24
-
Compare the Products:
- Since 24 is greater than 16, 3/16 is greater than 1/8.
Overall Conclusion
From the cross-multiplication comparisons:
- 1/4 > 1/8
- 1/4 > 3/16
- 3/16 > 1/8
This confirms that 1/4 is the largest fraction.
Real-World Examples and Applications
Understanding how to compare fractions isn't just a theoretical exercise; it has practical applications in everyday life. Here are a few examples:
-
Cooking:
- Imagine you are doubling a recipe that calls for 1/4 cup of sugar. You need to know how much sugar to add. Knowing that 1/4 is greater than 1/8 or 3/16 helps you accurately measure the ingredients.
-
Construction and Measurement:
- In construction, measurements often involve fractions. If you need to cut a piece of wood that is slightly larger than 1/8 inch but smaller than 1/4 inch, understanding these fractions helps you make precise cuts.
-
Financial Planning:
- When dealing with investments or loans, interest rates are often expressed as fractions. Comparing these fractions helps you understand which option offers the best value.
-
Time Management:
- If you need to allocate time for different tasks, understanding fractions can help you divide your time effectively. For example, if you spend 1/4 of your day working, 1/8 commuting, and 3/16 on other activities, knowing which fraction is larger helps you prioritize your time.
-
Sharing and Distribution:
- When sharing resources or dividing tasks among a group, fractions come into play. Understanding how to compare fractions ensures that everyone receives a fair share.
Common Mistakes to Avoid
When comparing fractions, it’s easy to make mistakes if you’re not careful. Here are some common pitfalls to watch out for:
-
Assuming Larger Denominator Means Larger Fraction:
- A common mistake is to assume that a fraction with a larger denominator is always smaller. While it's true that if the numerators are the same, a larger denominator means a smaller fraction, this isn't always the case when the numerators are different. For example, 3/16 is greater than 1/8 even though 16 is greater than 8.
-
Forgetting to Find a Common Denominator:
- When comparing fractions, it’s essential to convert them to equivalent fractions with a common denominator. Failing to do so can lead to incorrect comparisons.
-
Incorrectly Converting to Decimals:
- When converting fractions to decimals, make sure to perform the division accurately. A small error in the division can result in a wrong comparison.
-
Ignoring the Numerator:
- Always consider the numerator when comparing fractions. A larger denominator doesn't automatically mean the fraction is smaller; the numerator plays a crucial role.
-
Not Simplifying Fractions:
- Sometimes, simplifying fractions before comparing them can make the process easier. For example, if you have fractions like 2/4 and 1/2, simplifying 2/4 to 1/2 makes it immediately clear that they are equal.
Conclusion: 1/4, 1/8, or 3/16?
After exploring various methods including visual comparison, finding a common denominator, converting to decimals, and cross-multiplication, we've consistently found that 1/4 is the largest fraction among 1/4, 1/8, and 3/16. Each of these methods provides a different perspective on comparing fractions, and understanding them can help you confidently tackle similar problems in the future.
Comparing fractions is a fundamental skill with wide-ranging applications. Whether you're cooking, measuring, planning finances, or managing time, a solid understanding of fractions can make these tasks easier and more accurate.
What other math concepts would you like to explore? Do you have a favorite method for comparing fractions, or have you encountered any interesting real-world scenarios where comparing fractions was essential? Share your thoughts and experiences!
Latest Posts
Latest Posts
-
Difference Between A Solute And A Solvent
Nov 19, 2025
-
Choose All Characteristics Of Slow Twitch Fibers
Nov 19, 2025
-
How To Grow Germs In A Petri Dish
Nov 19, 2025
-
How Do Mycorrhizal Fungi Benefit Plants
Nov 19, 2025
-
Equation For Energy Of A Wave
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about Which Is Bigger 1/4 1/8 Or 3/16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.