What Is The Lcm Of 8 And 10
pythondeals
Nov 06, 2025 · 11 min read
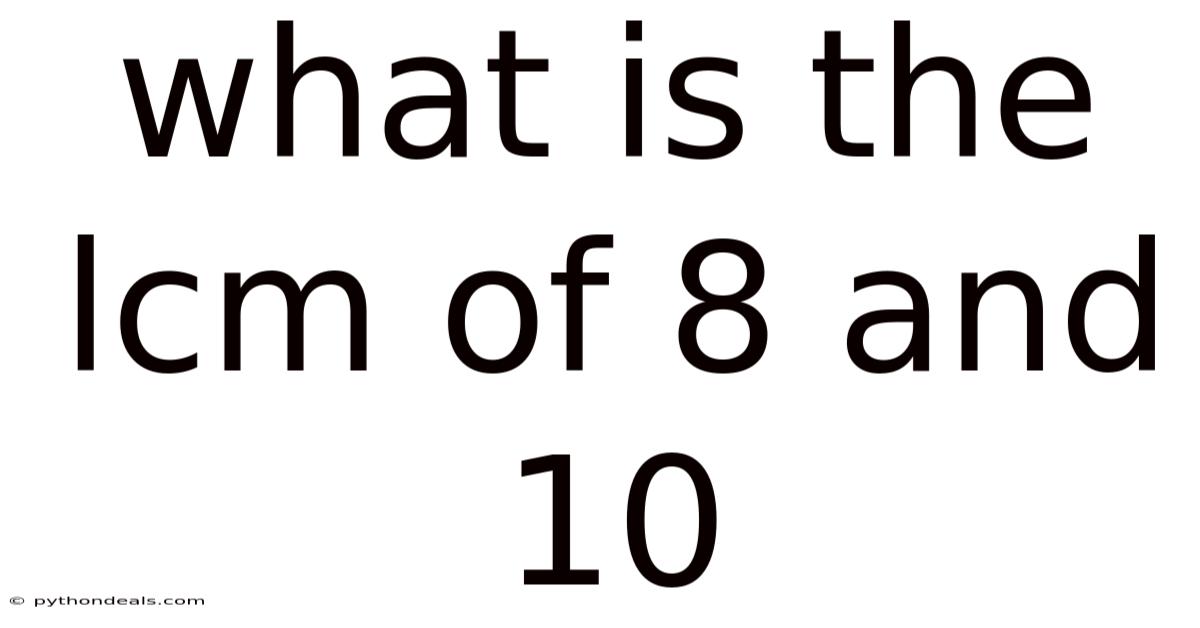
Table of Contents
Finding the Least Common Multiple (LCM) of two numbers is a fundamental skill in mathematics, particularly useful in arithmetic and algebra. The LCM is the smallest positive integer that is perfectly divisible by both numbers. In this comprehensive guide, we will explore the concept of LCM, its significance, various methods to calculate it, and apply these methods to find the LCM of 8 and 10. Whether you are a student, educator, or just someone looking to brush up on your math skills, this article will provide a thorough understanding of how to efficiently determine the LCM of any given set of numbers.
Understanding the Least Common Multiple (LCM)
The Least Common Multiple (LCM) is the smallest multiple that two or more numbers share. This concept is particularly useful when dealing with fractions, adding or subtracting fractions with different denominators, and solving problems involving cycles or periodic events.
Why is LCM Important?
- Fractions: The LCM is essential when adding or subtracting fractions with different denominators. By finding the LCM of the denominators, you can convert the fractions to equivalent fractions with a common denominator, making the addition or subtraction straightforward.
- Problem Solving: LCM is used in various real-world problems, such as determining when two events will occur simultaneously, calculating gear rotations, or optimizing schedules.
- Mathematical Foundation: Understanding LCM is crucial for more advanced mathematical concepts, including number theory and algebra.
Basic Definitions
- Multiple: A multiple of a number is the product of that number and any integer. For example, multiples of 8 are 8, 16, 24, 32, and so on.
- Common Multiple: A common multiple of two or more numbers is a multiple that is shared by all the numbers. For instance, common multiples of 8 and 10 include 40, 80, 120, and so on.
- Least Common Multiple (LCM): The smallest common multiple of two or more numbers is the LCM. For 8 and 10, the LCM is 40.
Methods to Calculate LCM
There are several methods to calculate the LCM of two or more numbers. We will discuss three common methods: listing multiples, prime factorization, and using the greatest common divisor (GCD).
Method 1: Listing Multiples
The simplest method to find the LCM is by listing the multiples of each number until a common multiple is found.
Steps:
- List Multiples: Write down the multiples of each number.
- Identify Common Multiples: Look for multiples that appear in both lists.
- Find the Least: Identify the smallest common multiple.
Example: Finding the LCM of 8 and 10
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
From the lists, the common multiples are 40, 80, and so on. The smallest of these is 40.
Therefore, the LCM of 8 and 10 is 40.
Advantages:
- Easy to understand and implement, especially for small numbers.
Disadvantages:
- Can be time-consuming and impractical for larger numbers, as it requires listing many multiples.
Method 2: Prime Factorization
Prime factorization involves breaking down each number into its prime factors and then using these factors to find the LCM.
Steps:
- Prime Factorization: Find the prime factorization of each number.
- Identify Highest Powers: Identify the highest power of each prime factor that appears in any of the factorizations.
- Multiply: Multiply these highest powers together to get the LCM.
Example: Finding the LCM of 8 and 10
- Prime factorization of 8: (2^3)
- Prime factorization of 10: (2 \times 5)
The prime factors are 2 and 5. The highest power of 2 is (2^3), and the highest power of 5 is (5^1).
LCM = (2^3 \times 5^1 = 8 \times 5 = 40)
Therefore, the LCM of 8 and 10 is 40.
Advantages:
- Systematic and efficient, especially for larger numbers.
- Provides a clear understanding of the numbers' composition.
Disadvantages:
- Requires knowledge of prime factorization, which may be challenging for some.
Method 3: Using the Greatest Common Divisor (GCD)
The Greatest Common Divisor (GCD) is the largest positive integer that divides two or more numbers without leaving a remainder. The LCM and GCD are related by the formula:
[ \text{LCM}(a, b) = \frac{|a \times b|}{\text{GCD}(a, b)} ]
Steps:
- Find GCD: Calculate the GCD of the two numbers.
- Multiply Numbers: Multiply the two numbers.
- Divide: Divide the product by the GCD to find the LCM.
Example: Finding the LCM of 8 and 10
First, we need to find the GCD of 8 and 10.
- Factors of 8: 1, 2, 4, 8
- Factors of 10: 1, 2, 5, 10
The greatest common divisor of 8 and 10 is 2.
Now, use the formula:
[ \text{LCM}(8, 10) = \frac{|8 \times 10|}{\text{GCD}(8, 10)} = \frac{80}{2} = 40 ]
Therefore, the LCM of 8 and 10 is 40.
Advantages:
- Useful if the GCD is known or easily calculated.
- Provides a mathematical relationship between LCM and GCD.
Disadvantages:
- Requires calculating the GCD first, which may involve additional steps.
Step-by-Step Calculation: Finding the LCM of 8 and 10
To illustrate each method more clearly, let's walk through the steps again, focusing on finding the LCM of 8 and 10.
Method 1: Listing Multiples
- List Multiples of 8:
- 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, ...
- List Multiples of 10:
- 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
- Identify Common Multiples:
- The common multiples are 40, 80, ...
- Find the Least Common Multiple:
- The smallest common multiple is 40.
Conclusion: The LCM of 8 and 10 using the listing multiples method is 40.
Method 2: Prime Factorization
- Prime Factorization of 8:
- 8 = 2 × 2 × 2 = (2^3)
- Prime Factorization of 10:
- 10 = 2 × 5
- Identify Highest Powers of Prime Factors:
- Highest power of 2: (2^3)
- Highest power of 5: (5^1)
- Multiply Highest Powers:
- LCM = (2^3 \times 5^1 = 8 \times 5 = 40)
Conclusion: The LCM of 8 and 10 using the prime factorization method is 40.
Method 3: Using the Greatest Common Divisor (GCD)
- Find the GCD of 8 and 10:
- Factors of 8: 1, 2, 4, 8
- Factors of 10: 1, 2, 5, 10
- The greatest common divisor is 2.
- Multiply the Numbers:
- 8 × 10 = 80
- Divide the Product by the GCD:
- LCM = (\frac{80}{2} = 40)
Conclusion: The LCM of 8 and 10 using the GCD method is 40.
Real-World Applications
Understanding and calculating the LCM is not just a theoretical exercise; it has practical applications in various real-world scenarios.
Example 1: Scheduling
Imagine you have two tasks: Task A needs to be done every 8 days, and Task B needs to be done every 10 days. If both tasks are done today, when is the next time they will both be done on the same day?
This is an LCM problem. Task A repeats every 8 days, and Task B repeats every 10 days. The LCM of 8 and 10 is 40, so both tasks will be done together again in 40 days.
Example 2: Fractions
When adding or subtracting fractions with different denominators, you need to find a common denominator. The LCM of the denominators is often the best choice for the common denominator because it is the smallest number that both denominators divide into evenly.
For example, to add (\frac{1}{8}) and (\frac{1}{10}), you need to find the LCM of 8 and 10, which is 40. Then, you can convert the fractions to:
[ \frac{1}{8} = \frac{5}{40} \quad \text{and} \quad \frac{1}{10} = \frac{4}{40} ]
Now, you can easily add the fractions:
[ \frac{5}{40} + \frac{4}{40} = \frac{9}{40} ]
Example 3: Gears
In mechanical engineering, gears with different numbers of teeth mesh together. The LCM is used to determine how many rotations each gear must make before they return to their starting positions.
If Gear A has 8 teeth and Gear B has 10 teeth, the LCM of 8 and 10 is 40. This means Gear A must make 5 rotations (40/8) and Gear B must make 4 rotations (40/10) before they both return to their original positions.
Advanced Tips and Tricks
- LCM of More Than Two Numbers: To find the LCM of more than two numbers, you can use the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor, and multiply these highest powers together.
- Using Online Calculators: There are many online calculators available that can quickly calculate the LCM of any set of numbers. These can be useful for checking your work or for dealing with very large numbers.
- Practice: The best way to master the LCM is to practice solving problems. Start with simple examples and gradually work your way up to more complex ones.
Common Mistakes to Avoid
- Confusing LCM with GCD: Make sure you understand the difference between LCM (the smallest common multiple) and GCD (the largest common divisor).
- Incorrect Prime Factorization: Double-check your prime factorizations to avoid errors.
- Missing Common Multiples: When listing multiples, make sure you list enough multiples to find the least common one.
- Arithmetic Errors: Be careful with your calculations, especially when multiplying and dividing large numbers.
The Underlying Mathematical Principles
The calculation of the LCM is rooted in fundamental mathematical principles, primarily related to number theory and divisibility. Understanding these principles can provide a deeper appreciation for the LCM and its applications.
Divisibility
A number ( a ) is divisible by a number ( b ) if the division ( a / b ) results in an integer with no remainder. The LCM of two numbers ( a ) and ( b ) is the smallest positive integer that is divisible by both ( a ) and ( b ).
Prime Numbers and Factorization
Prime numbers are integers greater than 1 that have no positive divisors other than 1 and themselves (e.g., 2, 3, 5, 7, 11). Every integer greater than 1 can be expressed as a product of prime numbers, a process known as prime factorization. This is a unique representation, which is fundamental to finding the LCM.
Euclidean Algorithm for GCD
The Euclidean algorithm is an efficient method for computing the GCD of two integers. It is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. The algorithm can be summarized as follows:
- Given two numbers ( a ) and ( b ), where ( a > b ), divide ( a ) by ( b ) to get a quotient ( q ) and a remainder ( r ), such that ( a = bq + r ).
- If ( r = 0 ), then GCD(( a, b )) = ( b ).
- If ( r \neq 0 ), replace ( a ) with ( b ) and ( b ) with ( r ), and repeat the process.
Using this algorithm, one can efficiently find the GCD, and subsequently, the LCM using the formula ( \text{LCM}(a, b) = \frac{|a \times b|}{\text{GCD}(a, b)} ).
FAQ (Frequently Asked Questions)
Q: What is the LCM used for in real life?
A: LCM is used in various applications, such as scheduling events, adding fractions with different denominators, and determining gear rotations in mechanical systems.
Q: Can the LCM of two numbers be smaller than both numbers?
A: No, the LCM of two numbers is always greater than or equal to the larger of the two numbers.
Q: Is there an easy way to find the LCM of large numbers?
A: The prime factorization method is generally the most efficient for large numbers. Online calculators can also be helpful.
Q: What is the relationship between LCM and GCD?
A: The LCM and GCD are related by the formula: (\text{LCM}(a, b) = \frac{|a \times b|}{\text{GCD}(a, b)}).
Q: How do I find the LCM of more than two numbers?
A: Use the prime factorization method. Find the prime factorization of each number, identify the highest power of each prime factor, and multiply these highest powers together.
Conclusion
The Least Common Multiple (LCM) is a crucial concept in mathematics with numerous practical applications. Whether you use the listing multiples method, prime factorization, or the GCD method, understanding how to calculate the LCM efficiently is essential for solving a variety of problems. For the specific case of finding the LCM of 8 and 10, all three methods converge to the same answer: 40.
By mastering these techniques and understanding the underlying principles, you can confidently tackle LCM problems and apply them to real-world scenarios. Keep practicing, and you'll find that calculating the LCM becomes second nature.
How do you plan to use your newfound knowledge of LCM? What other mathematical concepts would you like to explore further?
Latest Posts
Latest Posts
-
What Is The Difference Between Sympatric And Allopatric Speciation
Nov 06, 2025
-
What Are The 3 Basic Parts Of An Atom
Nov 06, 2025
-
Is Wedge Up Or Down Chemistry
Nov 06, 2025
-
What Is The Difference Between Celsius And Fahrenheit
Nov 06, 2025
-
What Is The Asthenosphere Composed Of
Nov 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.