What Is The Absolute Value Of -5
pythondeals
Nov 20, 2025 · 10 min read
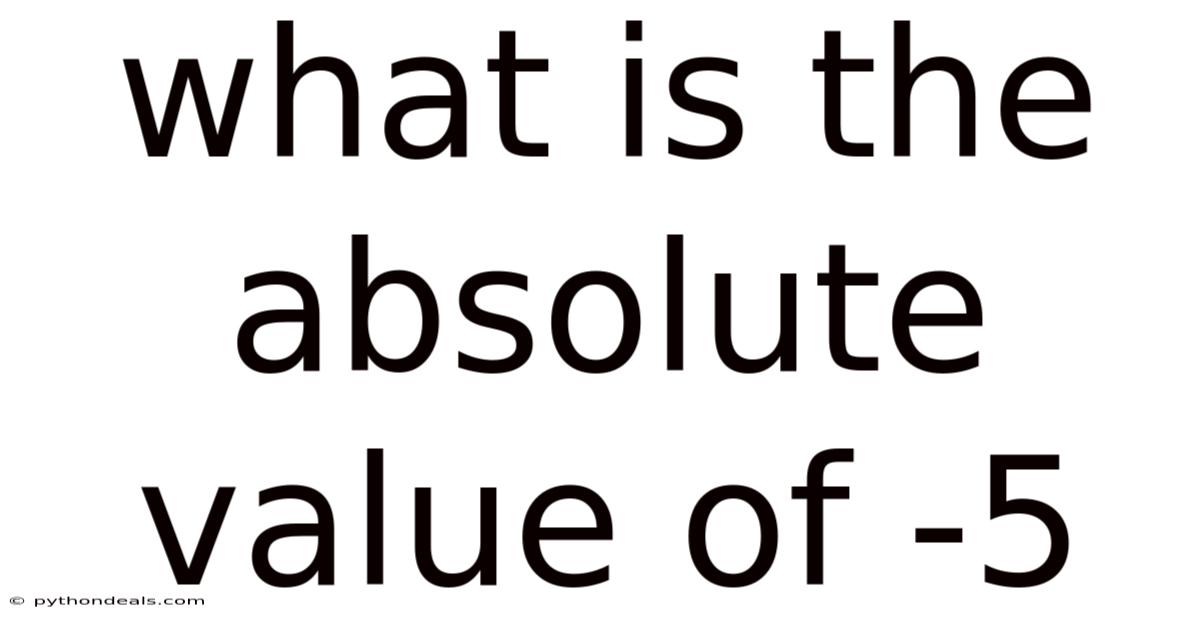
Table of Contents
The concept of absolute value, often represented by two vertical bars surrounding a number (e.g., |-5|), is fundamental in mathematics. It signifies the distance of a number from zero on the number line, regardless of direction. This distance is always non-negative, meaning it's either positive or zero. In simpler terms, the absolute value strips away the negative sign from negative numbers while leaving positive numbers unchanged. Understanding absolute value is crucial for various mathematical operations, including solving equations, graphing functions, and analyzing data. This article will delve into the intricacies of absolute value, exploring its definition, properties, applications, and its significance in more advanced mathematical concepts.
The question of "What is the absolute value of -5?" is a straightforward introduction to this concept. The absolute value of -5, denoted as |-5|, is simply 5. This means that -5 is 5 units away from zero on the number line. This simple example highlights the core principle of absolute value: to provide a measure of magnitude without considering direction. The absolute value function transforms any input into its non-negative equivalent. As we explore further, we'll uncover why this seemingly simple concept is so powerful and widely used in mathematics and its applications.
Comprehensive Overview of Absolute Value
Absolute value, at its core, is a function that maps real numbers to non-negative real numbers. Formally, for any real number x, the absolute value of x, denoted as |x|, is defined as follows:
- |x| = x, if x ≥ 0
- |x| = -x, if x < 0
This definition might seem a bit abstract, but it simply means that if x is a positive number or zero, its absolute value is x itself. If x is a negative number, its absolute value is the negation of x, which turns it into a positive number. For example, |7| = 7 because 7 is already positive, and |-3| = -(-3) = 3 because -3 is negative and its negation is positive.
Historical Context: The concept of absolute value, while not always explicitly named, has been implicitly used in mathematics for centuries. Early mathematicians encountered situations where they needed to consider the magnitude of a quantity without regard to its sign. For instance, when dealing with distances or errors in measurement, the sign of the error might be irrelevant; only the size of the error matters. The formal notation and definition of absolute value emerged more recently, solidifying its place as a distinct mathematical operation.
Geometric Interpretation: The geometric interpretation of absolute value provides an intuitive understanding of its meaning. Imagine the number line extending infinitely in both positive and negative directions from zero. The absolute value of a number x is the distance between the point representing x on the number line and the origin (zero). Distance is always a non-negative quantity, so the absolute value is always non-negative. For example, both 5 and -5 are 5 units away from zero, so their absolute values are both 5.
Properties of Absolute Value: Understanding the properties of absolute value is crucial for manipulating expressions and solving equations involving absolute values. Some key properties include:
- Non-negativity: |x| ≥ 0 for all real numbers x. This follows directly from the definition that absolute value returns a non-negative value.
- Symmetry: |x| = |-x| for all real numbers x. This property reflects the symmetry of the number line around zero. A number and its negation are equidistant from zero.
- Product: |xy| = |x| * |y| for all real numbers x and y. The absolute value of a product is the product of the absolute values. This property simplifies expressions involving products and absolute values.
- Quotient: |x / y| = |x| / |y| for all real numbers x and y (where y ≠ 0). Similar to the product property, the absolute value of a quotient is the quotient of the absolute values.
- Triangle Inequality: |x + y| ≤ |x| + |y| for all real numbers x and y. This property is called the triangle inequality because it relates to the sides of a triangle. It states that the absolute value of a sum is less than or equal to the sum of the absolute values.
- |x| ≤ a ⇔ -a ≤ x ≤ a: If the absolute value of x is less than or equal to a, then x is between -a and a.
- |x| ≥ a ⇔ x ≤ -a or x ≥ a: If the absolute value of x is greater than or equal to a, then x is either less than or equal to -a or greater than or equal to a.
These properties are essential tools for simplifying expressions, solving equations, and proving theorems involving absolute values. They allow us to manipulate absolute value expressions in a systematic and rigorous way.
Absolute Value in Equations and Inequalities: Absolute value plays a significant role in solving equations and inequalities. When solving equations involving absolute values, it's important to consider both the positive and negative cases. For example, to solve the equation |x| = 5, we need to find all values of x whose distance from zero is 5. This leads to two possible solutions: x = 5 and x = -5.
Similarly, when solving inequalities involving absolute values, we need to consider different cases depending on the sign of the expression inside the absolute value. For example, to solve the inequality |x| < 3, we need to find all values of x whose distance from zero is less than 3. This is equivalent to the compound inequality -3 < x < 3. The solution set is the interval (-3, 3). Understanding how to handle these different cases is crucial for correctly solving equations and inequalities involving absolute values.
Tren & Perkembangan Terbaru
While the fundamental definition of absolute value remains constant, its applications and the ways it's used in modern mathematics and computation continue to evolve. Here are some current trends and developments related to absolute value:
- Machine Learning and Optimization: Absolute value functions, particularly in forms like L1 regularization (using the sum of absolute values of coefficients), are increasingly used in machine learning for feature selection and model simplification. L1 regularization encourages sparsity in the model, effectively setting some coefficients to zero and thus eliminating irrelevant features.
- Robust Statistics: Absolute value is central to robust statistical methods that are less sensitive to outliers than traditional methods based on squared errors. The least absolute deviations (LAD) regression, for instance, minimizes the sum of absolute errors rather than the sum of squared errors, making it more resistant to the influence of extreme values in the data.
- Computer Graphics and Game Development: Absolute value is used to calculate distances and reflections, essential for simulating realistic physics and rendering visual effects. For example, it can be used to ensure that a virtual object bounces correctly off a surface.
- Control Theory: Absolute value functions are used to model systems with saturation or dead zones, where the output is limited or non-responsive within a certain input range.
- Financial Modeling: Absolute value is used in financial models to represent risk measures and to calculate the magnitude of gains and losses.
These applications show that absolute value is not just a theoretical concept but a practical tool used across a wide range of disciplines. As technology advances and new challenges arise, the importance and versatility of absolute value are likely to continue to grow.
Tips & Expert Advice
Here are some practical tips and advice for working with absolute values, based on common challenges and misconceptions:
- Always Consider Both Positive and Negative Cases: When solving equations or inequalities involving absolute values, remember to consider both the positive and negative possibilities for the expression inside the absolute value. This is the most common mistake students make. For example, when solving |x - 2| = 3, set up two equations: x - 2 = 3 and x - 2 = -3, and solve each separately.
- Isolate the Absolute Value Expression: Before splitting into cases, isolate the absolute value expression on one side of the equation or inequality. For example, if you have 2|x + 1| - 3 = 5, first add 3 to both sides and then divide by 2 to get |x + 1| = 4. Then, you can split into cases.
- Use Properties to Simplify: Utilize the properties of absolute value, such as the product and quotient rules, to simplify complex expressions before attempting to solve them. For instance, if you have |2x| = 6, you can use the product rule to rewrite it as |2| * |x| = 6, which simplifies to 2|x| = 6, and then |x| = 3.
- Be Careful with Inequalities: When dealing with inequalities, remember that |x| < a is equivalent to -a < x < a, while |x| > a is equivalent to x < -a or x > a. It's easy to mix these up, so take your time and write them out carefully.
- Visualize on the Number Line: If you're struggling to understand a problem involving absolute value, try visualizing it on the number line. This can help you see the distances and relationships between numbers more clearly.
- Check Your Solutions: After solving an equation or inequality involving absolute values, always check your solutions by plugging them back into the original problem to make sure they are valid. Sometimes, you may get extraneous solutions that don't actually work.
- Understand the Triangle Inequality: The triangle inequality, |x + y| ≤ |x| + |y|, is a powerful tool for proving other inequalities. Try to understand its geometric interpretation: the sum of the lengths of two sides of a triangle is always greater than or equal to the length of the third side.
By following these tips, you can avoid common mistakes and gain a deeper understanding of absolute value. Remember, practice is key. The more you work with absolute values, the more comfortable and confident you will become.
FAQ (Frequently Asked Questions)
Q: What is the absolute value of 0? A: The absolute value of 0 is 0. |0| = 0.
Q: Can the absolute value of a number be negative? A: No, the absolute value of a number is always non-negative (positive or zero).
Q: How do I solve an equation like |x + 3| = 7? A: You need to consider two cases: Case 1: x + 3 = 7, which gives x = 4. Case 2: x + 3 = -7, which gives x = -10. So, the solutions are x = 4 and x = -10.
Q: What is the difference between absolute value and just removing the negative sign? A: While it might seem like absolute value just removes the negative sign, it's more precise to say it gives the distance from zero. For positive numbers, it doesn't change anything.
Q: How is absolute value used in real life? A: Absolute value is used to measure distances, errors, and magnitudes without considering direction or sign. For example, measuring the error in a manufacturing process or calculating the distance traveled regardless of direction.
Q: Is there a symbol other than | | for absolute value? A: No, the standard notation for absolute value is the vertical bar symbol | |.
Conclusion
The absolute value of -5 is 5. This simple answer encapsulates the core concept of absolute value: it represents the distance of a number from zero, irrespective of its sign. The absolute value function transforms any input into its non-negative counterpart, making it a fundamental tool in mathematics and various other fields. We've explored the definition, properties, and applications of absolute value, highlighting its significance in solving equations, analyzing data, and modeling real-world phenomena. From machine learning to robust statistics, absolute value plays a crucial role in modern applications.
Understanding absolute value is essential for anyone studying mathematics or working in a related field. By grasping the underlying principles and practicing with different types of problems, you can develop a solid foundation for more advanced mathematical concepts. Remember to always consider both positive and negative cases when solving equations or inequalities involving absolute values, and utilize the properties to simplify complex expressions.
How has your understanding of absolute value changed after reading this article? What are some other real-world applications of absolute value that you can think of?
Latest Posts
Latest Posts
-
Content Analysis Focuses On What Aspect Of The Artwork
Nov 20, 2025
-
Characteristics Of A Species That Enable It To Survive
Nov 20, 2025
-
How To Do Elimination And Substitution
Nov 20, 2025
-
The Relationship Between Dna Genes And Chromosomes
Nov 20, 2025
-
What Is The Amdr For Fat
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about What Is The Absolute Value Of -5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.