What Is 4/6 In Simplest Form
pythondeals
Nov 16, 2025 · 8 min read
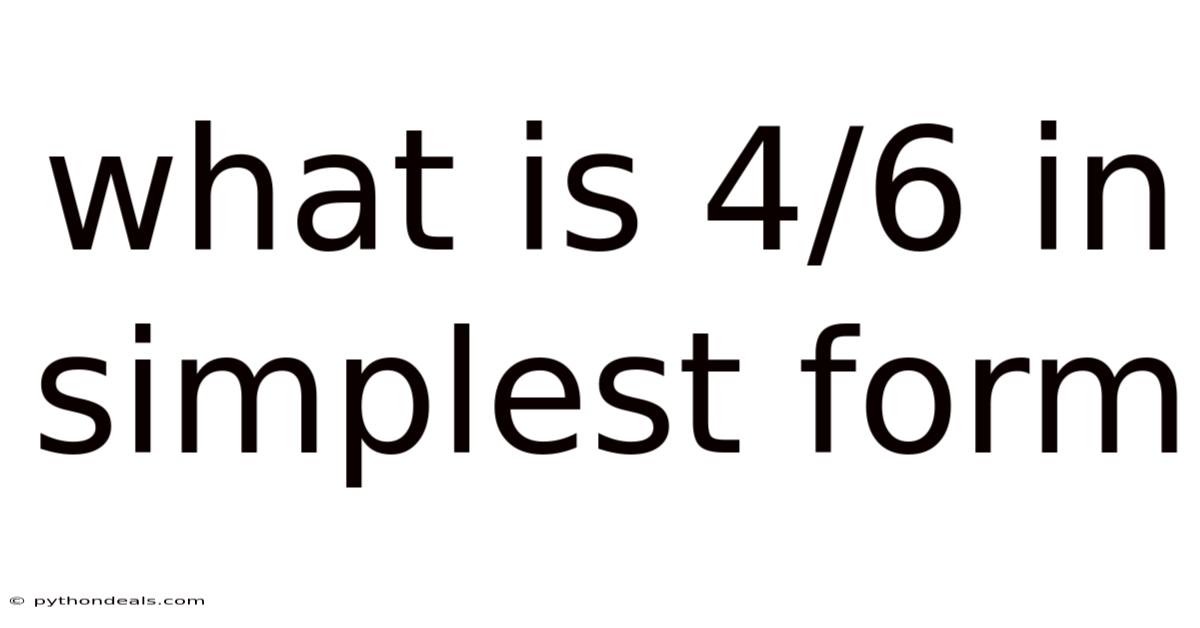
Table of Contents
Let's dive into the world of fractions and explore how to simplify them. Understanding fractions is a fundamental skill in mathematics, essential for everyday tasks like cooking, measuring, and even understanding financial concepts. When dealing with fractions, simplifying them to their simplest form makes them easier to understand and work with. One common fraction that often requires simplification is 4/6.
Simplifying fractions involves reducing them to their lowest terms, meaning that the numerator (the top number) and the denominator (the bottom number) are as small as possible while still representing the same value. Simplifying 4/6 isn’t just a mathematical exercise; it's a way to express the same quantity in a more concise and manageable form.
Understanding Fractions
Before we dive into simplifying 4/6, let's quickly recap what fractions are and why they are important. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The number on top of the fraction bar, indicating how many parts of the whole are being considered.
- Denominator: The number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 4/6:
- 4 is the numerator, representing four parts.
- 6 is the denominator, representing that the whole is divided into six equal parts.
Fractions are used everywhere. Imagine you're sharing a pizza cut into six slices, and you take four slices. You've taken 4/6 of the pizza. Now, what if you could express that amount more simply? That's where simplifying comes in.
What Does "Simplest Form" Mean?
The simplest form of a fraction is when the numerator and the denominator have no common factors other than 1. In other words, you cannot divide both the numerator and the denominator by the same number to get smaller whole numbers. This is also known as reducing the fraction to its lowest terms.
For instance, consider the fraction 2/4. Both 2 and 4 are divisible by 2. If we divide both by 2, we get 1/2. The fraction 1/2 is the simplest form of 2/4 because 1 and 2 have no common factors other than 1.
Simplifying fractions makes them easier to compare, add, subtract, multiply, and divide. It’s a fundamental skill that simplifies many mathematical operations.
Simplifying 4/6: A Step-by-Step Guide
Now, let’s get to the heart of the matter: simplifying the fraction 4/6. Here’s a step-by-step guide:
Step 1: Identify Common Factors
The first step in simplifying any fraction is to identify the common factors of the numerator and the denominator. A factor is a number that divides evenly into another number.
- Factors of 4: 1, 2, 4
- Factors of 6: 1, 2, 3, 6
From the lists above, we can see that both 4 and 6 share the common factors 1 and 2.
Step 2: Find the Greatest Common Factor (GCF)
The Greatest Common Factor (GCF) is the largest factor that both numbers share. In this case, the GCF of 4 and 6 is 2.
Step 3: Divide Both Numerator and Denominator by the GCF
Divide both the numerator and the denominator of the fraction by the GCF.
- Numerator: 4 ÷ 2 = 2
- Denominator: 6 ÷ 2 = 3
Step 4: Write the Simplified Fraction
The simplified fraction is the result of the division in the previous step.
- Simplified fraction: 2/3
So, 4/6 in its simplest form is 2/3.
Example:
Let’s say you have 4 slices of a cake that was originally cut into 6 slices. You have 4/6 of the cake. By simplifying, you realize you have the same amount as if the cake was cut into 3 slices and you took 2 of them.
Visualizing Fraction Simplification
Sometimes, visualizing fractions can make the concept easier to understand. Imagine a rectangle divided into 6 equal parts, with 4 of those parts shaded. This represents 4/6.
Now, imagine grouping those 6 parts into 3 equal sections. Each section would contain 2 original parts. The 4 shaded parts would now be 2 shaded sections out of the 3 total sections. This visually shows that 4/6 is equivalent to 2/3.
Visual aids like this can be particularly helpful for learners who are new to fractions or who benefit from seeing mathematical concepts in action.
Why Does This Work?
You might wonder why dividing both the numerator and the denominator by the same number doesn't change the value of the fraction. The reason is that you’re essentially multiplying the fraction by 1 in a disguised form.
In our example, we divided both 4 and 6 by 2. This is the same as multiplying the fraction 4/6 by (1/2) / (1/2). Since (1/2) / (1/2) equals 1, we’re not changing the value of the fraction, only its appearance.
Alternative Methods for Simplifying Fractions
While finding the GCF is a straightforward method, there are other ways to simplify fractions, especially if you have larger numbers.
Method 1: Repeated Division
If you don’t immediately see the GCF, you can divide the numerator and the denominator by any common factor you find. Then, continue dividing until no common factors remain.
Example: Simplify 24/36
- Notice that both 24 and 36 are divisible by 2:
- 24 ÷ 2 = 12
- 36 ÷ 2 = 18
- New fraction: 12/18
- Notice that both 12 and 18 are divisible by 2:
- 12 ÷ 2 = 6
- 18 ÷ 2 = 9
- New fraction: 6/9
- Notice that both 6 and 9 are divisible by 3:
- 6 ÷ 3 = 2
- 9 ÷ 3 = 3
- Simplified fraction: 2/3
Method 2: Prime Factorization
Prime factorization involves breaking down the numerator and denominator into their prime factors. Then, you can cancel out the common prime factors.
Example: Simplify 24/36
- Prime factorization of 24: 2 x 2 x 2 x 3
- Prime factorization of 36: 2 x 2 x 3 x 3
- Write the fraction with prime factors: (2 x 2 x 2 x 3) / (2 x 2 x 3 x 3)
- Cancel out common factors: (2 x 2 x
2x3) / (2 x 2 x3x 3) - Remaining factors: 2 / 3
- Simplified fraction: 2/3
Common Mistakes to Avoid
When simplifying fractions, there are a few common mistakes to watch out for:
- Forgetting to Divide Both Numerator and Denominator:
- Make sure you divide both the numerator and the denominator by the same number. Dividing only one will change the value of the fraction.
- Not Simplifying Completely:
- Always check if the simplified fraction can be simplified further. If the numerator and denominator still have a common factor, continue simplifying.
- Dividing by a Non-Factor:
- Ensure that the number you're dividing by is a factor of both the numerator and the denominator.
Real-World Applications
Understanding how to simplify fractions isn't just an abstract mathematical concept; it has practical applications in many real-world scenarios.
- Cooking:
- Recipes often call for fractions of ingredients. Simplifying these fractions can make measuring easier. For example, if a recipe calls for 4/6 of a cup of flour, you can simplify it to 2/3 of a cup.
- Measuring:
- When measuring lengths or distances, you might encounter fractions. Simplifying these fractions can provide a clearer understanding of the measurement.
- Financial Calculations:
- Fractions are used in financial calculations such as calculating interest rates or dividing profits. Simplifying these fractions can make the calculations more straightforward.
- Construction and Carpentry:
- In construction, measurements often involve fractions. Simplifying these fractions ensures accuracy and prevents errors.
- Time Management:
- Dividing tasks into fractions of time can help in time management. Simplifying these fractions can provide a clearer schedule.
Practice Problems
To solidify your understanding, here are a few practice problems:
- Simplify 6/8
- Simplify 9/12
- Simplify 10/15
- Simplify 12/18
- Simplify 16/20
Answers:
- 3/4
- 3/4
- 2/3
- 2/3
- 4/5
The Importance of Mastering Fractions
Mastering fractions is a critical step in mathematical education. Fractions are foundational to more advanced mathematical concepts like algebra, geometry, and calculus. A strong understanding of fractions builds confidence and competence in mathematics.
Moreover, the ability to work with fractions develops critical thinking and problem-solving skills. Simplifying fractions requires you to analyze numbers, identify patterns, and apply logical reasoning, skills that are valuable in many areas of life.
Fun Facts About Fractions
To make learning about fractions more engaging, here are a few fun facts:
- The word "fraction" comes from the Latin word "fractio," which means "to break."
- Ancient Egyptians were among the first to use fractions, over 4000 years ago.
- The fraction bar (the line between the numerator and denominator) is called a vinculum.
- Fractions can be used to represent probabilities. For example, if you flip a fair coin, the probability of getting heads is 1/2.
- The concept of fractions extends to more complex mathematical ideas like rational numbers and algebraic fractions.
Conclusion
Simplifying fractions is an essential skill that makes mathematical operations easier and provides a clearer understanding of quantities. In the case of 4/6, the simplest form is 2/3. By following the steps outlined in this article, you can confidently simplify fractions and apply this knowledge to various real-world scenarios. Whether you’re cooking, measuring, or solving complex mathematical problems, a solid understanding of fractions will serve you well.
How do you plan to use your new understanding of simplifying fractions in your daily life or studies? Are there any specific areas where you think this skill will be particularly helpful?
Latest Posts
Latest Posts
-
When An Image Crosses The Retina We Perceive
Nov 16, 2025
-
Chromosomes Are Duplicated During What Stage Of The Cell Cycle
Nov 16, 2025
-
Does Natural Selection Act On Individuals
Nov 16, 2025
-
What Causes Shifts In The Supply Curve
Nov 16, 2025
-
Strength Based Approach In Social Work
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/6 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.