What Are Two Fractions Equivalent To 2/3
pythondeals
Nov 19, 2025 · 9 min read
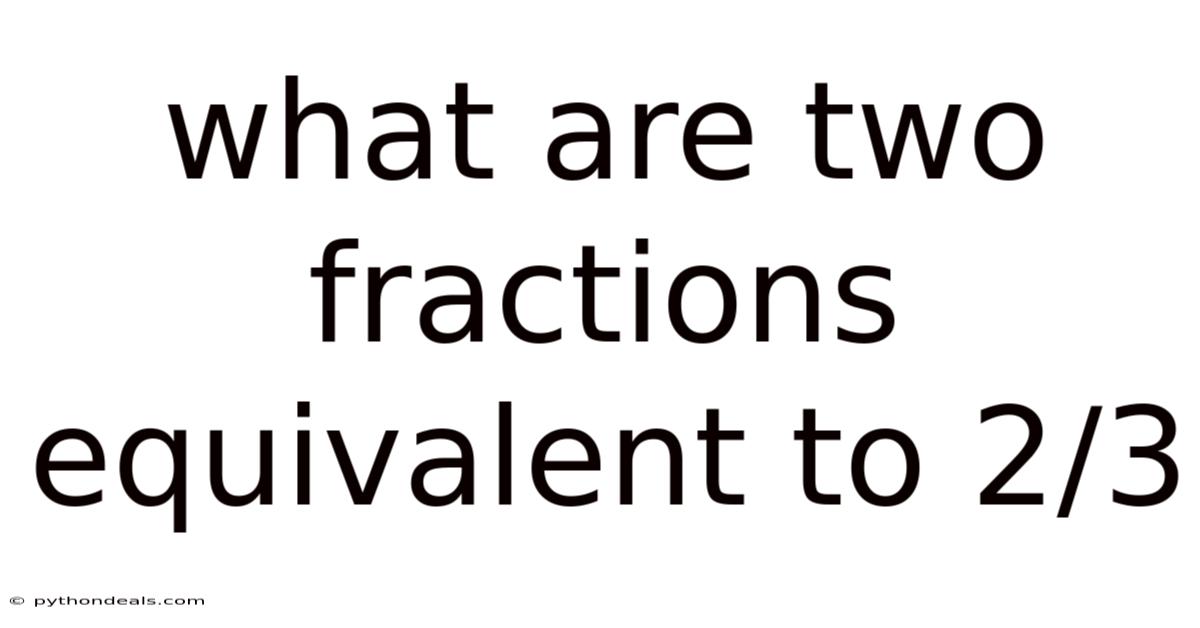
Table of Contents
Let's dive into the world of fractions and discover how to find fractions equivalent to 2/3. Understanding equivalent fractions is a fundamental concept in mathematics, essential not just for elementary school students, but also for anyone who needs to work with numbers in everyday life. Whether you’re baking a cake, splitting a bill, or designing a building, knowing how to manipulate fractions will make your calculations easier and more accurate.
Fractions represent parts of a whole, and equivalent fractions are different representations of the same proportion. The fraction 2/3 simply means we have two parts out of a total of three equal parts. While 2/3 is one way to express this quantity, there are infinitely many other fractions that represent the exact same value. We will explore methods to easily generate equivalent fractions and understand the underlying principles that make it possible.
Understanding Equivalent Fractions
Equivalent fractions are fractions that look different but represent the same value. For instance, 2/3 is equivalent to 4/6, 6/9, 8/12, and so on. These fractions, when simplified, all reduce to 2/3. Understanding this concept is crucial for several reasons:
- Simplifying Calculations: Sometimes, working with larger fractions can be cumbersome. By converting them to simpler, equivalent fractions, we can make calculations easier.
- Comparing Fractions: When we want to compare two fractions, it's often easiest to find a common denominator. This involves creating equivalent fractions with the same denominator, allowing for a straightforward comparison.
- Real-World Applications: In everyday scenarios, like cooking or measuring, being able to work with equivalent fractions ensures precision and avoids errors.
The key to finding equivalent fractions lies in the fundamental principle that multiplying or dividing both the numerator (the top number) and the denominator (the bottom number) by the same non-zero number doesn't change the fraction's value. This is because, in essence, we are multiplying or dividing the fraction by 1. Let’s delve deeper into why this principle holds true.
The Principle Behind Equivalent Fractions
When we multiply a fraction by a form of 1 (like 2/2, 3/3, 4/4, etc.), we are not changing its value, only its appearance. Consider the fraction 2/3. If we multiply both the numerator and the denominator by 2, we get:
(2 * 2) / (3 * 2) = 4/6
The fraction 4/6 is equivalent to 2/3 because it represents the same proportion. Imagine a pie cut into three slices, and you take two of them. Now, imagine you cut each of those three slices in half. You now have six slices, and you've taken four of them. You still have the same amount of pie, just cut into smaller pieces.
Similarly, division works in the same way. If you have a fraction like 6/9, you can divide both the numerator and the denominator by 3:
(6 / 3) / (9 / 3) = 2/3
Again, the value of the fraction remains unchanged. This principle is based on the multiplicative identity property, which states that any number multiplied by 1 remains unchanged. By multiplying or dividing both the numerator and denominator by the same number, we are essentially multiplying or dividing by a form of 1, thus preserving the original value.
Methods to Find Equivalent Fractions of 2/3
Now that we understand the underlying principle, let's explore some methods to find equivalent fractions of 2/3.
1. Multiplication Method
The most straightforward method is to multiply both the numerator and the denominator by the same whole number. Let's find two equivalent fractions using this method:
-
First Equivalent Fraction: Multiply both the numerator and denominator of 2/3 by 4:
(2 * 4) / (3 * 4) = 8/12
So, 8/12 is equivalent to 2/3.
-
Second Equivalent Fraction: Multiply both the numerator and denominator of 2/3 by 7:
(2 * 7) / (3 * 7) = 14/21
Thus, 14/21 is another fraction equivalent to 2/3.
2. Division Method (Simplifying Fractions)
Sometimes, you might start with a larger fraction and want to find its simplest equivalent form. In this case, you would divide both the numerator and the denominator by their greatest common divisor (GCD). However, since 2/3 is already in its simplest form (2 and 3 have no common factors other than 1), we cannot simplify it further. But, if we were given a fraction like 4/6, we could divide both numbers by 2 to get 2/3.
Examples of Equivalent Fractions of 2/3
To further illustrate the concept, let's generate a few more equivalent fractions of 2/3:
- Multiply by 2: (2 * 2) / (3 * 2) = 4/6
- Multiply by 3: (2 * 3) / (3 * 3) = 6/9
- Multiply by 5: (2 * 5) / (3 * 5) = 10/15
- Multiply by 10: (2 * 10) / (3 * 10) = 20/30
- Multiply by 25: (2 * 25) / (3 * 25) = 50/75
Each of these fractions represents the same value as 2/3. You can verify this by converting each fraction to a decimal. For instance, 2/3 ≈ 0.6667, 4/6 ≈ 0.6667, 6/9 ≈ 0.6667, and so on.
Practical Applications of Equivalent Fractions
Understanding and using equivalent fractions is not just an academic exercise; it has numerous practical applications in everyday life.
- Cooking: Recipes often need to be adjusted to serve more or fewer people. If a recipe calls for 2/3 cup of flour and you want to double the recipe, you need to find an equivalent fraction that represents double the amount. In this case, you would need 4/6 cup, which simplifies to 2/3 * 2 = 4/3 or 1 1/3 cups.
- Measuring: In construction and carpentry, precise measurements are crucial. If you need to cut a piece of wood to 2/3 of a foot, you might find it easier to measure 8/12 of a foot using inches.
- Financial Calculations: When splitting bills or calculating percentages, equivalent fractions can simplify the process. For example, if you need to divide a bill equally among three people and one person pays 2/3 of their share upfront, you need to calculate how much more they owe.
- Map Reading: Maps often use scales that involve fractions. Understanding equivalent fractions helps in converting map distances to real-world distances accurately.
Common Mistakes to Avoid
While finding equivalent fractions is relatively straightforward, there are a few common mistakes that students and others sometimes make.
- Adding Instead of Multiplying: A common mistake is to add the same number to both the numerator and the denominator. For example, adding 1 to both the numerator and denominator of 2/3 gives 3/4, which is not equivalent to 2/3.
- Only Changing One Number: Another mistake is to only multiply or divide the numerator or the denominator, but not both. This changes the value of the fraction.
- Forgetting to Simplify: Sometimes, you might find an equivalent fraction, but it’s not in its simplest form. Always try to simplify the fraction to its lowest terms to make it easier to work with.
Advanced Concepts Related to Equivalent Fractions
Once you have a solid understanding of equivalent fractions, you can move on to more advanced concepts, such as:
- Cross-Multiplication: This is a method to check if two fractions are equivalent. If a/b = c/d, then ad = bc. For example, to check if 2/3 is equivalent to 4/6, multiply 2 * 6 and 3 * 4. Both equal 12, so the fractions are equivalent.
- Ratio and Proportion: Equivalent fractions are closely related to the concepts of ratio and proportion. Understanding these concepts is crucial for solving problems involving scaling, percentages, and comparisons.
- Algebraic Fractions: In algebra, fractions can involve variables. The same principles of finding equivalent fractions apply, but you need to use algebraic manipulation to find equivalent expressions.
Real-World Examples in Different Fields
The concept of equivalent fractions extends far beyond basic arithmetic. It is applied in various fields, enabling professionals to handle complex problems efficiently.
Engineering: Engineers use fractions to represent various aspects of design and construction. For example, when designing a bridge, engineers must calculate loads and stresses, often expressed as fractions. Understanding equivalent fractions allows them to simplify these calculations and ensure structural integrity.
Finance: Financial analysts use fractions and percentages extensively. When calculating investment returns or analyzing market trends, equivalent fractions help in converting different representations of the same data, making analysis more straightforward.
Computer Science: In computer graphics, fractions are used to represent color values (e.g., RGB values). Understanding equivalent fractions is essential for color manipulation and ensuring that colors remain consistent across different displays.
Music: Music theory relies heavily on fractions. Musical notes and rhythms are often expressed as fractions of a whole, and understanding equivalent fractions is crucial for composing and playing music accurately.
Why Equivalent Fractions Matter in Standardized Tests
Equivalent fractions are a staple in standardized tests such as the SAT, ACT, and GRE. Questions involving fractions often require students to simplify, compare, or perform operations on fractions. Mastering equivalent fractions is essential for achieving high scores on these tests.
Test-Taking Strategies: When faced with fraction-related questions, students should first try to simplify the fractions to their simplest form. This often makes the problem easier to solve. Additionally, understanding how to convert fractions to decimals and vice versa can be helpful in certain situations.
FAQ (Frequently Asked Questions)
-
Q: Are 3/5 and 6/10 equivalent fractions?
- A: Yes, 3/5 and 6/10 are equivalent fractions. You can multiply both the numerator and denominator of 3/5 by 2 to get 6/10.
-
Q: Can equivalent fractions have different denominators?
- A: Yes, equivalent fractions can have different denominators as long as they represent the same value. For example, 1/2 and 2/4 are equivalent fractions with different denominators.
-
Q: How do you find the simplest form of a fraction?
- A: To find the simplest form of a fraction, divide both the numerator and denominator by their greatest common divisor (GCD).
-
Q: Is it possible to find an infinite number of equivalent fractions for any given fraction?
- A: Yes, it is possible to find an infinite number of equivalent fractions for any given fraction by multiplying both the numerator and the denominator by different whole numbers.
Conclusion
Finding equivalent fractions of 2/3 is a fundamental skill that opens the door to a deeper understanding of mathematics and its applications. By understanding the principle of multiplying or dividing both the numerator and the denominator by the same number, you can easily generate equivalent fractions. This knowledge is not just useful for academic purposes but also has numerous practical applications in everyday life, from cooking and measuring to financial calculations and more.
Remember, practice makes perfect. The more you work with fractions and equivalent fractions, the more comfortable and confident you will become. So, go ahead and explore the world of fractions, and you’ll find it to be a valuable and rewarding journey.
How do you plan to use your newfound knowledge of equivalent fractions in your daily life? Are there any specific areas where you think this understanding will be particularly helpful?
Latest Posts
Latest Posts
-
Before Administering The Medication Providers Should
Nov 19, 2025
-
Alternating Current Frequency Is Measured In
Nov 19, 2025
-
Origin And Insertion Of Muscles Definition
Nov 19, 2025
-
Is Air A Type Of Matter
Nov 19, 2025
-
What Differences Between Plant And Animal Cells
Nov 19, 2025
Related Post
Thank you for visiting our website which covers about What Are Two Fractions Equivalent To 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.