Value Of R In Pv Nrt
pythondeals
Nov 28, 2025 · 11 min read
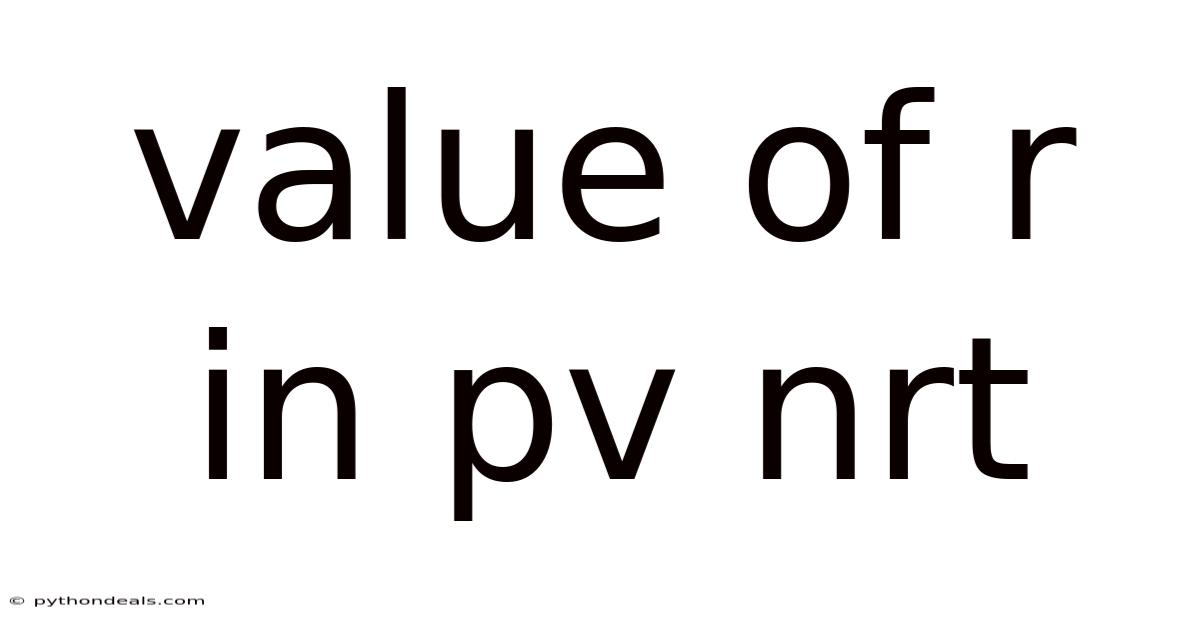
Table of Contents
Alright, let's dive into the significance of 'R' in the ideal gas law, PV=nRT. We'll explore its meaning, its different forms, how it impacts calculations, and why it's so crucial in various scientific and engineering applications.
Introduction: Unveiling the Universal Gas Constant
Imagine you're experimenting with different gases, measuring their pressure, volume, temperature, and the amount of substance. You might notice a consistent relationship emerging between these properties. This consistency is captured by the ideal gas law, PV = nRT. Here, 'R,' the universal gas constant, acts as a bridge connecting these seemingly disparate variables. Understanding its value and units is critical to accurately predicting gas behavior. It's a foundational concept that impacts fields ranging from chemistry and physics to engineering and atmospheric science.
The ideal gas law is a cornerstone of thermodynamics and provides a simplified model for understanding the behavior of gases under certain conditions. It assumes that gas particles have negligible volume and that there are no intermolecular forces between them. While these assumptions aren't perfectly true for real gases, the ideal gas law provides a remarkably accurate approximation for many practical applications. The universal gas constant, 'R,' is the linchpin of this equation, ensuring that the units on both sides of the equation are consistent and that the relationship holds true for all ideal gases.
Delving into the Ideal Gas Law: PV = nRT
Before we deep-dive into the specifics of 'R,' let's quickly recap the ideal gas law itself.
- P stands for pressure, usually measured in Pascals (Pa), atmospheres (atm), or bars.
- V represents volume, typically measured in cubic meters (m³) or liters (L).
- n denotes the number of moles of the gas, indicating the amount of substance.
- T is the absolute temperature, always measured in Kelvin (K).
- And, of course, R is the universal gas constant.
The equation PV = nRT states that for a given amount of gas (n) at a specific temperature (T), the product of its pressure (P) and volume (V) is directly proportional to the temperature and the number of moles. The constant of proportionality is none other than 'R.'
What is the Universal Gas Constant (R)?
The universal gas constant (R) is a physical constant that relates the energy scale to the temperature scale when dealing with gases. It's derived from the experimental observation that one mole of any ideal gas occupies approximately the same volume at the same temperature and pressure. This volume is about 22.4 liters at standard temperature and pressure (STP), defined as 0 °C (273.15 K) and 1 atmosphere (101.325 kPa).
Essentially, 'R' is a scaling factor that ensures the consistency of units when using the ideal gas law. Its value depends on the units used for pressure, volume, and temperature.
The Many Faces of R: Different Values and Units
One of the trickiest aspects of working with the ideal gas law is choosing the correct value of 'R.' This depends entirely on the units you're using for pressure, volume, and temperature. Here's a breakdown of the most common values:
-
R = 8.314 J/(mol·K) (Joules per mole Kelvin). This value is used when pressure is in Pascals (Pa) and volume is in cubic meters (m³). The units are derived from the fact that pressure times volume (PV) has units of energy (Joules). This is the most versatile value as it is expressed in SI units.
-
R = 0.0821 L·atm/(mol·K) (Liters times atmospheres per mole Kelvin). This value is used when pressure is in atmospheres (atm) and volume is in liters (L). This is commonly used in chemistry due to the convenience of working with liters and atmospheres in lab settings.
-
R = 1.987 cal/(mol·K) (Calories per mole Kelvin). This value is used when energy is measured in calories.
-
R = 8.314 m³·Pa/(mol·K) (Cubic meters times Pascals per mole Kelvin). This is equivalent to the first value, simply expressing the units explicitly.
-
R = 62.36 L·Torr/(mol·K) or L·mmHg/(mol·K) (Liters times Torr or millimeters of mercury per mole Kelvin). This is used when pressure is measured in Torr or mmHg.
It is crucial to select the 'R' value that matches the units of your other variables. Using the wrong value will lead to significant errors in your calculations. Always double-check your units before plugging values into the ideal gas law!
Illustrative Examples: Putting R into Practice
Let's work through a few examples to see how the value of 'R' is used in real calculations.
Example 1: Calculating Volume
Problem: Suppose you have 2 moles of an ideal gas at a pressure of 1.5 atm and a temperature of 300 K. What is the volume of the gas?
Solution:
- Identify the known variables:
- n = 2 moles
- P = 1.5 atm
- T = 300 K
- Choose the appropriate value of R: Since the pressure is in atmospheres, we'll use R = 0.0821 L·atm/(mol·K).
- Rearrange the ideal gas law to solve for V: V = nRT/P
- Plug in the values: V = (2 mol) * (0.0821 L·atm/(mol·K)) * (300 K) / (1.5 atm)
- Calculate: V = 32.84 L
Therefore, the volume of the gas is approximately 32.84 liters.
Example 2: Calculating Pressure
Problem: A container holds 5 moles of an ideal gas at a volume of 10 L and a temperature of 25 °C. What is the pressure in Pascals?
Solution:
- Identify the known variables:
- n = 5 moles
- V = 10 L = 0.01 m³ (Conversion is important!)
- T = 25 °C = 298.15 K (Convert to Kelvin!)
- Choose the appropriate value of R: Since we want the pressure in Pascals and the volume is in cubic meters, we'll use R = 8.314 J/(mol·K).
- Rearrange the ideal gas law to solve for P: P = nRT/V
- Plug in the values: P = (5 mol) * (8.314 J/(mol·K)) * (298.15 K) / (0.01 m³)
- Calculate: P = 1,239,029.1 Pa (approximately) or 1239 kPa
Therefore, the pressure of the gas is approximately 1,239,029.1 Pascals.
Example 3: Using Different Units for R and Converting Back
Problem: You have 3 moles of gas in a volume of 5 liters at 280 K. Calculate the pressure in atmospheres using R = 0.0821 L atm / (mol K). Convert the result to Pascals.
Solution:
- Identify the known variables:
- n = 3 mol
- V = 5 L
- T = 280 K
- Using R = 0.0821 L atm / (mol K), calculate the pressure in atmospheres:
- P = nRT/V = (3 mol) * (0.0821 L atm / (mol K)) * (280 K) / (5 L) = 13.74 atm
- Convert atmospheres to Pascals:
- 1 atm = 101325 Pa
- P (in Pascals) = 13.74 atm * 101325 Pa/atm = 1392235.5 Pa
Therefore, the pressure is 13.74 atmospheres or approximately 1,392,236 Pascals. This demonstrates the importance of understanding how to convert between units.
The Theoretical Foundation of R
The value of 'R' can be derived theoretically from the kinetic theory of gases and the concept of molar volume at standard temperature and pressure (STP). According to the kinetic theory, the average kinetic energy of gas molecules is directly proportional to the absolute temperature. Furthermore, at STP, one mole of any ideal gas occupies approximately 22.4 liters.
Combining these concepts with the ideal gas law allows us to calculate the value of 'R'. It's important to remember that 'R' is a fundamental constant that reflects the underlying relationship between energy, temperature, and the amount of substance in a gas.
Beyond Ideal Gases: Real Gases and Deviations
While the ideal gas law is a powerful tool, it's important to recognize its limitations. Real gases deviate from ideal behavior, especially at high pressures and low temperatures. This is because the assumptions of negligible particle volume and no intermolecular forces are no longer valid under these conditions.
Various modifications to the ideal gas law, such as the Van der Waals equation, have been developed to account for these deviations. These equations introduce correction factors that consider the finite volume of gas molecules and the attractive forces between them. Even when using these more complex equations, the concept of 'R' as a bridge between macroscopic and microscopic properties remains fundamental.
The Importance of Accurate Measurements and Unit Consistency
The accuracy of any calculation involving the ideal gas law depends on the precision of the measurements of pressure, volume, temperature, and the number of moles. Inaccurate measurements will lead to errors in the calculated results, regardless of how accurately the value of 'R' is known.
Furthermore, as we've emphasized, maintaining consistency in units is absolutely critical. Always convert all variables to a consistent set of units before plugging them into the ideal gas law. Failing to do so is a very common source of error.
Applications of the Ideal Gas Law and R
The ideal gas law and the universal gas constant have a wide range of applications in various scientific and engineering fields:
- Chemistry: Calculating the molar mass of a gas, determining the volume of gas produced in a chemical reaction, and studying the stoichiometry of gas-phase reactions.
- Physics: Understanding the behavior of gases in thermodynamic systems, analyzing the properties of the atmosphere, and studying the principles of fluid mechanics.
- Engineering: Designing and optimizing chemical reactors, calculating the flow rate of gases in pipelines, and developing engines and turbines.
- Atmospheric Science: Modeling atmospheric processes, predicting weather patterns, and studying the effects of climate change.
Recent Trends and Developments
While the fundamental principles of the ideal gas law remain unchanged, ongoing research continues to refine our understanding of gas behavior. Advanced computational methods are being used to model the properties of real gases with greater accuracy, and new experimental techniques are being developed to measure gas properties under extreme conditions.
Furthermore, the ideal gas law is playing an increasingly important role in the development of new technologies, such as hydrogen fuel cells and carbon capture and storage systems.
Expert Tips for Working with R
- Memorize the most common values of R: It's helpful to have the values of R in SI units (8.314 J/(mol·K)) and L·atm/(mol·K) memorized.
- Always check your units: Before plugging values into the ideal gas law, double-check that all variables are expressed in consistent units.
- Convert to Kelvin: Always use absolute temperature (Kelvin) in your calculations.
- Be aware of the limitations of the ideal gas law: Remember that real gases deviate from ideal behavior under certain conditions.
- Use a calculator with unit conversion capabilities: This can help you avoid errors when converting between different units.
- Practice, practice, practice: The more you work with the ideal gas law, the more comfortable you'll become with using the correct value of R and avoiding common mistakes.
FAQ about the Value of R in PV=nRT
-
Q: Why is R called the "universal" gas constant?
- A: Because it applies to all ideal gases, regardless of their chemical identity.
-
Q: Can I use the ideal gas law for liquids or solids?
- A: No, the ideal gas law is only applicable to gases under conditions where they approximate ideal behavior.
-
Q: What happens if I use the wrong value of R?
- A: Your calculated result will be incorrect. The magnitude of the error will depend on how different the value of R you used is from the correct value.
-
Q: Is R a dimensionless constant?
- A: No, R has units. The units depend on the units used for pressure, volume, temperature, and the number of moles.
-
Q: How do I choose which value of R to use?
- A: The choice depends entirely on the units used for pressure and volume in your problem. Match the units of R to the units of P and V.
Conclusion: The Indispensable Role of R
The universal gas constant, 'R,' is much more than just a number in an equation. It's a fundamental constant that reflects the relationship between energy, temperature, and the amount of substance in a gas. Understanding its value, its different forms, and its applications is essential for anyone working with gases in science or engineering.
By carefully considering the units of your variables and choosing the appropriate value of 'R,' you can confidently use the ideal gas law to accurately predict gas behavior and solve a wide range of problems. Remember to always double-check your units and be aware of the limitations of the ideal gas law when dealing with real gases.
What are your biggest challenges when working with the ideal gas law? And, have you ever made a mistake by using the wrong value of R? I'd love to hear about your experiences in the comments below!
Latest Posts
Latest Posts
-
Cuantos Segundos Hay En Un Ano
Nov 28, 2025
-
What Does Q Represent In Chemistry
Nov 28, 2025
-
Which Is Greater 5 8 Or 3 4
Nov 28, 2025
-
The Correct Order Of Phases Of The Cell Cycle Is
Nov 28, 2025
-
Find The Area Of A Triangle With Fractions
Nov 28, 2025
Related Post
Thank you for visiting our website which covers about Value Of R In Pv Nrt . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.