Sum Of I From 1 To N
pythondeals
Nov 23, 2025 · 11 min read
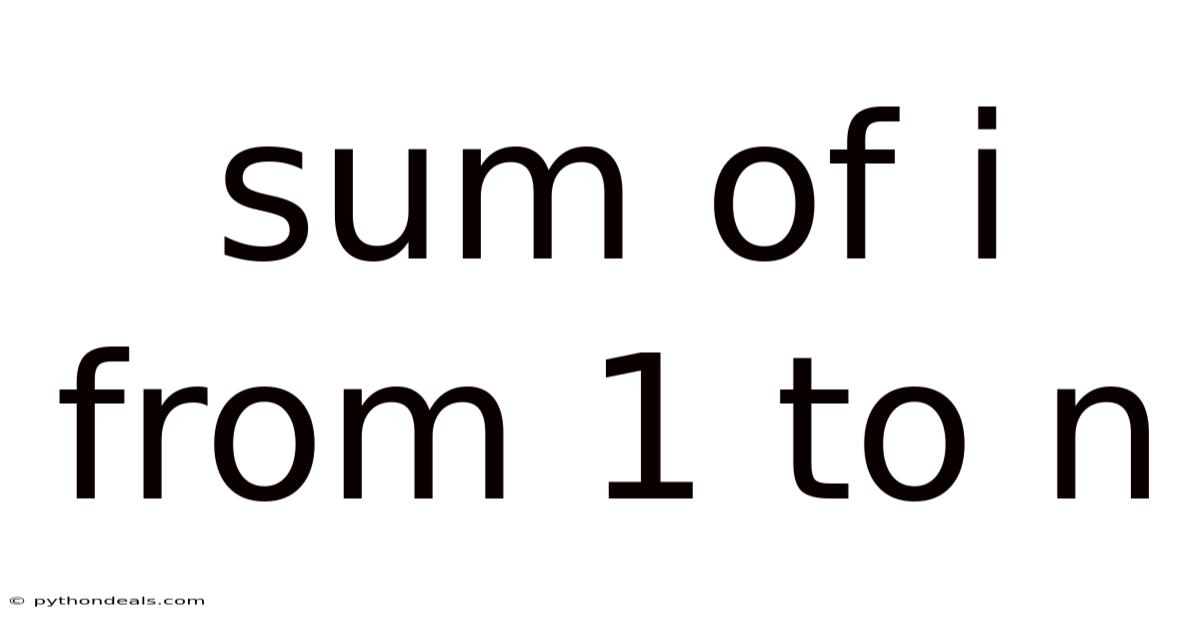
Table of Contents
Let's dive into the fascinating world of series and sequences, specifically focusing on the sum of integers from 1 to n. This fundamental concept forms the bedrock of various mathematical and computational applications, ranging from basic arithmetic to advanced algorithm design. Whether you're a student grappling with algebra, a programmer optimizing code, or simply a curious mind seeking mathematical insights, understanding this concept is invaluable.
Think about it: adding up the numbers from 1 to 10. It seems straightforward, but what about 1 to 100, or even 1 to 1,000,000? Manually summing those numbers would be incredibly tedious and error-prone. Fortunately, mathematics provides us with an elegant and efficient solution: a concise formula that allows us to calculate the sum directly. This article explores this formula, its origins, proofs, and practical applications, ensuring you grasp the concept of the sum of i from 1 to n thoroughly.
The Formula: A Quick Overview
The sum of consecutive integers from 1 to n is given by the following formula:
Sum = n * (n + 1) / 2
This formula allows us to calculate the sum without actually adding each individual number. Let's break down this formula and understand its significance. For example, if n = 10, the sum would be 10 * (10 + 1) / 2 = 55. This saves significant time and effort compared to adding 1 + 2 + 3 + ... + 10 manually.
Unveiling the Origins: Gauss and the Arithmetic Series
The story behind the discovery of this formula is quite remarkable and often attributed to the legendary mathematician Carl Friedrich Gauss. As a young student, Gauss was challenged to sum the integers from 1 to 100. While his classmates painstakingly began adding the numbers sequentially, Gauss quickly devised a brilliant shortcut.
He noticed that pairing the numbers in a specific way yielded consistent sums:
- 1 + 100 = 101
- 2 + 99 = 101
- 3 + 98 = 101
And so on. He realized there would be 50 such pairs, each summing to 101. Therefore, the total sum would be 50 * 101 = 5050.
This insightful observation led to the generalization of the formula for the sum of an arithmetic series. An arithmetic series is a sequence of numbers in which the difference between consecutive terms is constant. The sequence 1, 2, 3, ..., n is a special case of an arithmetic series where the common difference is 1.
The general formula for the sum of an arithmetic series is:
Sum = (n/2) * (first term + last term)
In our case, the first term is 1 and the last term is n. Plugging these values into the general formula, we get:
Sum = (n/2) * (1 + n)
Which is equivalent to our original formula:
Sum = n * (n + 1) / 2
Proving the Formula: Methods of Verification
While the story of Gauss provides a compelling narrative, it's essential to rigorously prove the formula using mathematical methods. Here are a few common approaches:
1. Mathematical Induction:
Mathematical induction is a powerful technique used to prove statements that hold for all natural numbers. It involves two main steps:
- Base Case: Show that the statement is true for the smallest possible value (usually n = 1).
- Inductive Step: Assume that the statement is true for some arbitrary value k (the inductive hypothesis) and then prove that it must also be true for k + 1.
Let's apply mathematical induction to prove the formula for the sum of integers from 1 to n.
-
Base Case (n = 1):
The sum of integers from 1 to 1 is simply 1. Plugging n = 1 into the formula, we get:
Sum = 1 * (1 + 1) / 2 = 1
Thus, the formula holds true for the base case.
-
Inductive Step:
Assume that the formula is true for some arbitrary value k. That is, assume:
1 + 2 + 3 + ... + k = k * (k + 1) / 2 (Inductive Hypothesis)
Now, we need to prove that the formula is also true for k + 1. That is, we need to show that:
1 + 2 + 3 + ... + k + (k + 1) = (k + 1) * ((k + 1) + 1) / 2
Starting with the left-hand side of the equation:
1 + 2 + 3 + ... + k + (k + 1)
Using the inductive hypothesis, we can substitute the sum of integers from 1 to k:
k * (k + 1) / 2 + (k + 1)
Now, we need to manipulate this expression to arrive at the right-hand side of the equation. Factoring out (k + 1):
(k + 1) * (k/2 + 1)
Finding a common denominator:
(k + 1) * (k/2 + 2/2)
(k + 1) * (k + 2) / 2
Which is exactly the right-hand side of the equation:
(k + 1) * ((k + 1) + 1) / 2
Therefore, we have shown that if the formula is true for k, it is also true for k + 1.
Since we have proven the base case and the inductive step, we can conclude by mathematical induction that the formula for the sum of integers from 1 to n is true for all natural numbers n.
2. Visual Proof (Geometric Approach):
Another elegant way to visualize and understand the formula is through a geometric approach. Imagine representing each number from 1 to n as a stack of blocks. For example, 1 would be a stack of 1 block, 2 would be a stack of 2 blocks, and so on.
Now, arrange these stacks of blocks in a staircase pattern. You'll notice that this staircase forms roughly half of a rectangle.
To complete the rectangle, create an identical staircase and flip it over, placing it alongside the original staircase. You now have a complete rectangle with dimensions n (width) and n + 1 (height).
The area of this rectangle is n * (n + 1). However, remember that this rectangle is made up of two identical staircases, each representing the sum of integers from 1 to n. Therefore, the area of one staircase (the sum we're looking for) is half the area of the rectangle:
Sum = n * (n + 1) / 2
This visual proof provides an intuitive understanding of why the formula works.
3. Algebraic Manipulation:
We can also prove the formula using purely algebraic manipulation. Let S represent the sum of integers from 1 to n:
S = 1 + 2 + 3 + ... + (n - 2) + (n - 1) + n
Now, write the same sum in reverse order:
S = n + (n - 1) + (n - 2) + ... + 3 + 2 + 1
Add these two equations together term by term:
2S = (1 + n) + (2 + (n - 1)) + (3 + (n - 2)) + ... + ((n - 2) + 3) + ((n - 1) + 2) + (n + 1)
Notice that each term in parentheses sums to n + 1. There are n such terms. Therefore:
2S = n * (n + 1)
Divide both sides by 2 to solve for S:
S = n * (n + 1) / 2
This algebraic proof provides a straightforward and concise derivation of the formula.
Practical Applications: Beyond the Classroom
The formula for the sum of integers from 1 to n isn't just a theoretical exercise; it has numerous practical applications in various fields:
-
Computer Science:
- Algorithm Analysis: When analyzing the time complexity of certain algorithms, particularly those involving nested loops, this formula often arises. For example, consider an algorithm that iterates i times for i ranging from 1 to n. The total number of iterations can be calculated using the formula.
- Data Structures: Understanding this summation is useful in working with specific data structures and their properties.
- Calculating Memory Allocation: In some scenarios, the amount of memory needed might grow linearly. This formula could help to estimate the total memory required.
-
Statistics:
- Calculating Averages: The formula can be used as a step in calculating the average of a consecutive set of numbers.
- Probability: Certain probability problems might involve summing probabilities that follow an arithmetic progression.
-
Physics:
- Kinematics: Problems involving uniformly accelerated motion might require calculating the sum of distances traveled over discrete time intervals.
-
Finance:
- Simple Interest Calculations: While not a direct application, understanding arithmetic series is foundational to more complex financial calculations.
-
Game Development:
- Level Design: Distributing resources or enemies across levels in a game might involve using this formula to ensure a balanced difficulty curve.
- Scoring Systems: Designing scoring systems where points increase incrementally can leverage this formula for calculating total scores.
Examples in Code:
Let's see how the formula can be used in a programming context. Here are examples in Python:
# Using the formula to calculate the sum
def sum_of_integers(n):
"""Calculates the sum of integers from 1 to n using the formula."""
return n * (n + 1) // 2 # Integer division to ensure an integer result
# Example usage:
n = 100
total_sum = sum_of_integers(n)
print(f"The sum of integers from 1 to {n} is: {total_sum}") # Output: 5050
# A more verbose approach (for comparison)
def sum_of_integers_iterative(n):
"""Calculates the sum of integers from 1 to n using iteration."""
total = 0
for i in range(1, n + 1):
total += i
return total
# Compare the performance of both methods (formula vs. iteration)
import time
n = 100000 # Larger value for performance comparison
start_time = time.time()
sum_formula = sum_of_integers(n)
end_time = time.time()
formula_time = end_time - start_time
start_time = time.time()
sum_iterative = sum_of_integers_iterative(n)
end_time = time.time()
iterative_time = end_time - start_time
print(f"Formula time: {formula_time:.6f} seconds")
print(f"Iterative time: {iterative_time:.6f} seconds")
# Assert that both methods produce the same result
assert sum_formula == sum_iterative
The Python code demonstrates how the formula is significantly faster than an iterative approach, especially for larger values of n. This highlights the practical benefit of understanding and using the formula in situations where performance is critical.
Common Misconceptions and Pitfalls
While the formula itself is relatively straightforward, there are a few common misconceptions and potential pitfalls to be aware of:
-
Starting Point: The formula is specifically for the sum of integers starting from 1. If you need to sum a series of consecutive integers starting from a different number (e.g., 5 to 15), you'll need to adjust the formula accordingly. You can do this by calculating the sum from 1 to 15 and then subtracting the sum from 1 to 4.
-
Non-Integer Values: The formula is designed for integer values of n. Applying it to non-integer values will yield incorrect results.
-
Overflow Errors: When dealing with very large values of n, be mindful of potential integer overflow errors in programming. Use appropriate data types (e.g.,
longin Java or larger integer types in other languages) to prevent these errors. -
Misunderstanding the Arithmetic Series: Ensure you understand the concept of an arithmetic series and its general formula. The
n*(n+1)/2formula is a specific case of the more general formula.
FAQs
Q: What is the sum of integers from 1 to 0?
A: The sum of integers from 1 to 0 is 0. The formula n(n+1)/2 works even for n = 0, resulting in 0*(0+1)/2 = 0. This is consistent with the idea that summing no numbers results in zero.
Q: Can the formula be used for negative integers?
A: The standard formula is designed for positive integers. If you need to sum consecutive negative integers from -1 to -n, you can simply multiply the result of the standard formula by -1. So, the sum from -1 to -n would be -(n(n+1)/2).
Q: How do I calculate the sum of even numbers from 2 to n?
A: You can factor out a 2 from the series: 2 + 4 + 6 + ... + n = 2 * (1 + 2 + 3 + ... + n/2). Then, apply the standard formula to the series inside the parentheses: 2 * [(n/2) * (n/2 + 1) / 2]. Simplifying, you get (n/2) * (n/2 + 1) or n*(n+2)/8. This formula assumes that n is even.
Q: Is there a formula for the sum of squares (1^2 + 2^2 + ... + n^2)?
A: Yes, the formula for the sum of squares is: n(n + 1)(2n + 1) / 6.
Q: How can I remember this formula easily?
A: Think of Gauss's pairing trick. You're essentially averaging the first and last term (1 and n) which gives you (n+1)/2, and then multiplying it by the number of terms, n.
Conclusion
The sum of integers from 1 to n, given by the formula n * (n + 1) / 2, is a fundamental concept with far-reaching applications. From its historical roots in Gauss's clever observation to its practical uses in computer science, statistics, and beyond, understanding this formula empowers you with a valuable tool for problem-solving and analytical thinking. We have explored its origins, provided rigorous proofs, and demonstrated its versatility through various examples.
By mastering this concept, you gain a deeper appreciation for the elegance and power of mathematics, and you'll be better equipped to tackle more complex challenges in your academic and professional pursuits.
How will you apply this knowledge to solve problems in your field? Are you interested in exploring other mathematical series and their fascinating properties?
Latest Posts
Latest Posts
-
What Is The Role Of Mrna In Translation
Nov 23, 2025
-
What Is Identity Property In Mathematics
Nov 23, 2025
-
Which Orbital Is The Last To Fill
Nov 23, 2025
-
How Many Electrons Does Au Have
Nov 23, 2025
-
Derivatives Of Log And Exponential Functions
Nov 23, 2025
Related Post
Thank you for visiting our website which covers about Sum Of I From 1 To N . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.