Square Root Of 1 X 2
pythondeals
Nov 27, 2025 · 9 min read
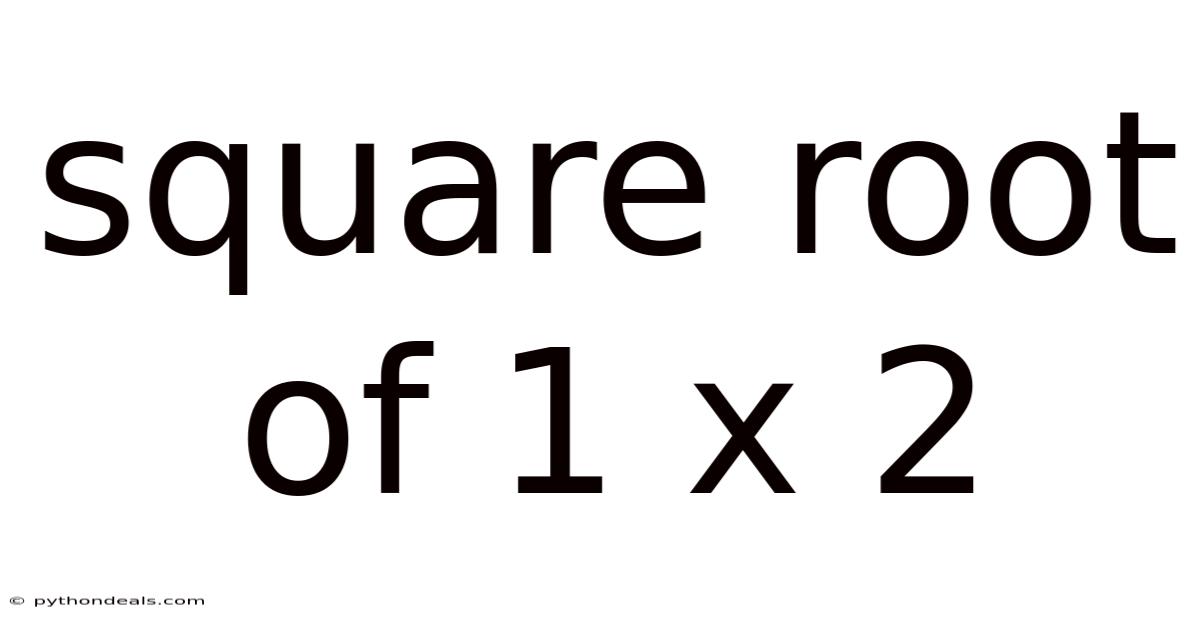
Table of Contents
Let's explore the square root of 1 x 2, diving into its basic calculation, relevance in mathematics, and common applications. This might seem like a straightforward concept, but understanding its intricacies is crucial for grasping more complex mathematical problems.
Understanding the Basics: Square Root of 1 x 2
At its core, the square root of 1 x 2 involves two fundamental mathematical operations: multiplication and finding a square root. It's essential to address the multiplication first, followed by the square root operation. The expression "1 x 2" simply means "1 multiplied by 2," which equals 2.
Therefore, the problem boils down to finding the square root of 2. Mathematically, this is represented as √2. The square root of a number x is a value y such that y times y (or y squared) equals x. In this case, we seek a number that, when multiplied by itself, gives us 2.
The square root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction a/b, where a and b are integers. Its decimal representation goes on infinitely without repeating. The approximate value of √2 is 1.41421356...
This seemingly simple calculation is a cornerstone of mathematics, appearing in various fields from geometry to computer science. Understanding how to calculate and interpret square roots is invaluable for anyone studying these subjects.
Comprehensive Overview: Square Roots in Mathematics
Square roots hold a significant place in the mathematical landscape. To fully appreciate the square root of 1 x 2 (√2), it’s useful to delve into the broader concept of square roots and their properties.
-
Definition and Notation: The square root of a number x is denoted as √x. Formally, if y² = x, then y is the square root of x.
-
Rational vs. Irrational Numbers: As mentioned earlier, √2 is an irrational number. Rational numbers can be expressed as a fraction of two integers, whereas irrational numbers cannot. The discovery of irrational numbers like √2 was a pivotal moment in the history of mathematics, challenging early assumptions about the nature of numbers.
-
Properties of Square Roots: Square roots have several properties that make them useful in mathematical manipulations:
- √(a * b) = √a * √b (The square root of a product is the product of the square roots.)
- √(a / b) = √a / √b (The square root of a quotient is the quotient of the square roots.)
- √(a²) = |a| (The square root of a number squared is the absolute value of that number.)
-
Geometric Interpretation: The square root also has a geometric interpretation. If you have a square with an area of x, then the length of each side of the square is √x. For example, if you have a square with an area of 2 square units, then each side has a length of √2 units.
-
Historical Significance: The concept of square roots dates back to ancient civilizations. The Babylonians, for example, had methods for approximating square roots as early as 1800 BC. The Greeks further developed the theory of square roots, particularly in the context of geometry. The discovery of irrational numbers like √2 is often attributed to the Pythagoreans, who initially found it unsettling because it didn't fit their belief that all numbers could be expressed as ratios of integers.
-
Methods for Calculating Square Roots: There are several methods for calculating square roots, ranging from manual techniques to algorithmic approaches:
- Babylonian Method: This is an iterative method that involves making an initial guess and then refining it through successive approximations.
- Long Division Method: A traditional method for calculating square roots by hand.
- Newton-Raphson Method: A more general iterative method that can be used to find the roots of various equations, including square roots.
- Using Calculators and Computers: Today, most people rely on calculators or computers to find square roots quickly and accurately. These devices use sophisticated algorithms to provide precise results.
Why is the Square Root of 2 (√2) Important?
The square root of 2 is not just an abstract mathematical concept; it has practical implications and appears in various real-world scenarios.
-
Geometry: √2 is famously known as the length of the diagonal of a square with sides of length 1. This relationship is a direct consequence of the Pythagorean theorem (a² + b² = c²). If you have a right triangle with both legs equal to 1, then the hypotenuse (diagonal) is √(1² + 1²) = √2.
-
Construction and Architecture: In fields such as construction and architecture, precise measurements are crucial. √2 is used in calculations involving diagonal lengths, ensuring accuracy in building structures. It is also vital in designing symmetrical and proportional structures.
-
Trigonometry: In trigonometry, √2 appears in the context of 45-45-90 triangles. The ratio of the sides in a 45-45-90 triangle is 1:1:√2, which is fundamental in various trigonometric calculations.
-
Computer Science: In computer graphics and image processing, √2 is used in calculations related to diagonal movements, pixel distances, and image scaling.
-
Navigation: √2 can be used in basic navigation and pathfinding scenarios, particularly when dealing with grid-based systems. For instance, in a square grid, moving diagonally involves a distance proportional to √2.
-
Engineering: In engineering disciplines, √2 is used in various calculations related to mechanics, electronics, and structural analysis. For example, it appears in the calculation of alternating current (AC) power and voltage.
Tren & Perkembangan Terbaru
In recent years, the computational aspects of irrational numbers like √2 have seen significant advancements due to increased computing power and sophisticated algorithms.
-
High-Precision Computation: Mathematicians and computer scientists continue to compute √2 to increasingly higher levels of precision. As of the latest computations, √2 has been calculated to trillions of digits, pushing the boundaries of computational capability.
-
Quantum Computing: Quantum computing may eventually offer more efficient algorithms for approximating irrational numbers. While still in its early stages, quantum computing holds the promise of solving complex mathematical problems more quickly than classical computers.
-
Machine Learning: Machine learning algorithms are being used to identify patterns and structures in the decimal expansion of irrational numbers like √2. Although these numbers are non-repeating and non-terminating, machine learning techniques can help in understanding their statistical properties.
-
Educational Tools: Modern educational software and apps provide interactive tools for exploring square roots and irrational numbers. These tools help students visualize concepts and develop a deeper understanding.
-
Cryptography: While √2 itself is not directly used in cryptography, the broader mathematical concepts related to irrational numbers and number theory play a crucial role in modern encryption algorithms.
Tips & Expert Advice
Understanding and working with square roots can be made easier with the right strategies. Here are some tips to help you master the square root of 2 and related concepts:
-
Memorize Key Values: Memorizing the approximate value of √2 (1.414) can be helpful for quick estimations. Knowing these values can speed up problem-solving in exams or practical situations.
-
Practice Manual Calculations: Even if you primarily use calculators, practice calculating square roots manually using methods like the Babylonian method or long division. This exercise enhances your understanding of the underlying principles.
-
Use Geometric Visualizations: When dealing with problems involving square roots, try to visualize them geometrically. For example, imagine a square with an area of 2 to understand the length of its sides as √2.
-
Apply Properties of Square Roots: Learn and apply the properties of square roots to simplify expressions. For instance, use √(a * b) = √a * √b to break down complex square root problems into simpler parts.
-
Check Your Answers: Always verify your calculations, especially in exams. Use estimation or reverse operations to ensure that your answers are reasonable. For example, if you find that √2 ≈ 1.5, you should realize that (1.5)² = 2.25, which is significantly different from 2, indicating a mistake.
-
Use Technology Wisely: While calculators and software can be helpful, understand their limitations. Be aware of rounding errors and precision issues, especially when dealing with irrational numbers.
-
Explore Advanced Topics: Once you have a good grasp of the basics, explore advanced topics related to square roots, such as complex numbers and algebraic manipulations involving square roots.
-
Relate to Real-World Applications: Connecting square roots to real-world applications can make learning more engaging. Look for examples in geometry, physics, engineering, and other fields.
FAQ (Frequently Asked Questions)
Q: What is the square root of 1 x 2?
A: The square root of 1 x 2 (which is the square root of 2) is approximately 1.414.
Q: Why is the square root of 2 irrational?
A: The square root of 2 is irrational because it cannot be expressed as a simple fraction a/b, where a and b are integers. Its decimal representation goes on infinitely without repeating.
Q: How do you calculate the square root of 2 without a calculator?
A: You can use methods like the Babylonian method or long division to approximate the square root of 2 manually.
Q: Where does the square root of 2 appear in geometry?
A: The square root of 2 is the length of the diagonal of a square with sides of length 1. It also appears in the ratios of sides in a 45-45-90 triangle.
Q: Is it important to memorize the value of the square root of 2?
A: Memorizing the approximate value of √2 (1.414) can be helpful for quick estimations and problem-solving.
Q: Can the square root of 2 be calculated exactly?
A: No, the square root of 2 is an irrational number, so its decimal representation goes on infinitely without repeating. We can only approximate its value to a certain degree of precision.
Q: How is the square root of 2 used in computer science?
A: In computer graphics and image processing, √2 is used in calculations related to diagonal movements, pixel distances, and image scaling.
Conclusion
The square root of 1 x 2, equivalent to √2, serves as a fundamental concept in mathematics, with far-reaching implications in fields like geometry, engineering, and computer science. Its irrational nature and precise calculation have fascinated mathematicians for centuries, leading to the development of numerous methods for approximation and computation. Understanding √2 not only enriches one's mathematical knowledge but also provides practical tools for problem-solving in various real-world scenarios.
As technology advances, our ability to compute and utilize irrational numbers like √2 will continue to grow, opening new avenues for innovation and discovery. Whether you're a student, an engineer, or simply a curious mind, exploring the intricacies of √2 offers valuable insights into the beauty and complexity of mathematics.
How do you feel about the significance of irrational numbers in modern technology, and what other mathematical concepts do you find equally fascinating?
Latest Posts
Latest Posts
-
Who Calculated The Mass Of An Electron
Nov 27, 2025
-
According To Marx Class Conflict Is
Nov 27, 2025
-
Words With Ed At The End
Nov 27, 2025
-
Who Said Religion Is The Opiate Of The Masses
Nov 27, 2025
-
Calculate Resonant Frequency Of Rlc Circuit
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.