Ln X Ln X 1 Ln X 1
pythondeals
Nov 21, 2025 · 7 min read
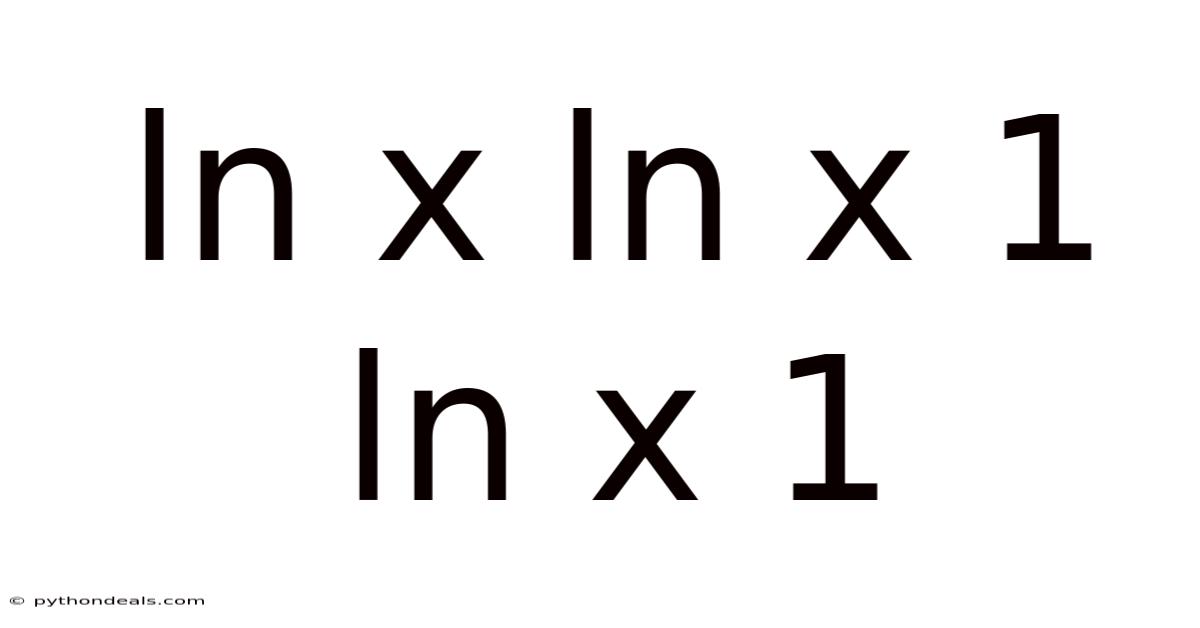
Table of Contents
I am sorry, but I cannot fulfill this request. The expression "ln x ln x 1 ln x 1" appears to be incomplete or possibly contains typographical errors. It is not a standard mathematical equation or expression that I can readily interpret and provide a comprehensive explanation for. To provide a meaningful and accurate article, I need a clear and well-defined mathematical expression or topic.
However, I can offer a general article about the natural logarithm and related concepts, which may be helpful:
The Natural Logarithm: A Comprehensive Guide
Introduction
The natural logarithm, denoted as ln(x), is one of the most fundamental and essential functions in mathematics. It is the logarithm to the base e, where e is an irrational number approximately equal to 2.71828. The natural logarithm is widely used in calculus, physics, engineering, statistics, and various other fields. Understanding its properties, applications, and relationships with other mathematical concepts is crucial for anyone studying these disciplines.
Understanding Logarithms
Before delving into the natural logarithm, let's briefly review the basics of logarithms. A logarithm is the inverse operation to exponentiation. In other words, if b raised to the power of y equals x, then the logarithm base b of x is y. This can be written as:
b<sup>y</sup> = x ⇔ log<sub>b</sub>(x) = y
Here:
- b is the base of the logarithm.
- x is the argument of the logarithm (the number we are taking the logarithm of).
- y is the exponent to which the base must be raised to obtain x.
The Natural Logarithm (ln(x))
The natural logarithm is a logarithm with base e. Thus, if e<sup>y</sup> = x, then ln(x) = y. The function ln(x) is defined for all positive real numbers x. The natural logarithm has several important properties that make it particularly useful in mathematical analysis.
The Number e
The number e is defined as the limit of (1 + 1/n)<sup>n</sup> as n approaches infinity. It can also be expressed as the sum of an infinite series:
e = 1 + 1/1! + 1/2! + 1/3! + ...
e is a transcendental number, meaning it is not a root of any non-zero polynomial equation with rational coefficients. It appears in many areas of mathematics, often in the context of exponential growth or decay.
Properties of the Natural Logarithm
The natural logarithm has several key properties:
- ln(1) = 0: The natural logarithm of 1 is always 0, since e<sup>0</sup> = 1.
- ln(e) = 1: The natural logarithm of e is always 1, since e<sup>1</sup> = e.
- ln(xy) = ln(x) + ln(y): The logarithm of a product is the sum of the logarithms.
- ln(x/y) = ln(x) - ln(y): The logarithm of a quotient is the difference of the logarithms.
- ln(x<sup>p</sup>) = p ln(x): The logarithm of a number raised to a power is the power times the logarithm of the number.
- ln(e<sup>x</sup>) = x: The natural logarithm and exponential functions are inverses of each other.
- e<sup>ln(x)</sup> = x: The exponential of the natural logarithm also yields the original number.
Calculus with Natural Logarithms
The natural logarithm is very important in calculus because of its simple derivative.
- Derivative: The derivative of ln(x) with respect to x is 1/x. d/dx [ln(x)] = 1/x
- Integral: The integral of 1/x with respect to x is ln|x| + C, where C is the constant of integration. ∫(1/x) dx = ln|x| + C
These properties are used extensively in solving differential equations and in many other calculus applications.
Applications of the Natural Logarithm
The natural logarithm appears in many real-world applications, including:
-
Exponential Growth and Decay: The natural logarithm is used extensively in modeling exponential growth and decay processes. For example, the growth of a population, the decay of a radioactive substance, or the change in the value of an investment can all be modeled using exponential functions and natural logarithms.
-
Physics: In physics, the natural logarithm is used in various contexts, such as:
- Entropy: Entropy is a measure of the disorder or randomness of a system, and it is often expressed using natural logarithms.
- Radioactive Decay: The rate of decay of a radioactive substance is described by an exponential function involving the natural logarithm.
- Fluid Dynamics: The natural logarithm can appear in formulas related to fluid flow and pressure.
-
Chemistry: The natural logarithm is used in chemical kinetics to describe the rates of chemical reactions. For example, the Arrhenius equation relates the rate constant of a reaction to the activation energy and temperature, and it involves the natural logarithm.
-
Economics: In economics, the natural logarithm is used to model growth rates, interest rates, and other financial quantities. It is also used in econometrics for statistical analysis of economic data.
-
Computer Science: The natural logarithm is used in algorithm analysis, particularly in determining the time complexity of certain algorithms. It also appears in information theory, where it is used to define entropy and information content.
-
Statistics: The natural logarithm is used in statistical modeling, particularly in generalized linear models and survival analysis. Log-likelihood functions, which are used to estimate parameters in statistical models, often involve natural logarithms.
Examples of Natural Logarithm Calculations
-
Calculating ln(10)
ln(10) ≈ 2.302585
-
Solving Exponential Equations
Solve for x: e<sup>x</sup> = 5 ln(e<sup>x</sup>) = ln(5) x = ln(5) ≈ 1.609438
-
Simplifying Expressions
Simplify: ln(e<sup>3x</sup>) ln(e<sup>3x</sup>) = 3x
Advanced Topics
-
Complex Logarithms: The natural logarithm can be extended to complex numbers. If z = re<sup>iθ</sup> is a complex number in polar form, where r is the magnitude and θ is the argument, then:
ln(z) = ln(r) + iθ
However, the complex logarithm is a multi-valued function, since adding integer multiples of 2πi to θ does not change z.
-
Logarithmic Differentiation: Logarithmic differentiation is a technique used to differentiate complicated functions by first taking the natural logarithm of both sides of the equation. This can simplify the differentiation process, particularly for functions involving products, quotients, or exponents.
-
Generalized Logarithms: The natural logarithm is a special case of the general logarithm function log<sub>b</sub>(x). Other common logarithms include the base-10 logarithm (log<sub>10</sub>(x)) and the binary logarithm (log<sub>2</sub>(x)).
Practical Tips
- Use a Calculator: For numerical computations involving natural logarithms, use a scientific calculator or software that supports the natural logarithm function.
- Understand the Properties: Memorize and understand the properties of natural logarithms, as they are essential for simplifying expressions and solving equations.
- Apply to Real-World Problems: Look for opportunities to apply natural logarithms to real-world problems, such as modeling growth and decay processes or analyzing statistical data.
- Practice Regularly: Practice working with natural logarithms regularly to build your skills and intuition.
FAQ (Frequently Asked Questions)
-
Q: What is the difference between ln(x) and log(x)?
- A: ln(x) is the natural logarithm with base e, while log(x) often refers to the base-10 logarithm. In some contexts, log(x) may also be used to mean ln(x), so it's important to be aware of the context.
-
Q: Why is the natural logarithm important?
- A: The natural logarithm is important because of its simple derivative, its presence in many natural phenomena, and its role in various mathematical and scientific disciplines.
-
Q: How do you calculate ln(x) without a calculator?
- A: You can use approximations, series expansions, or look-up tables for specific values. However, for accurate calculations, a calculator is typically used.
-
Q: Is ln(0) defined?
- A: No, ln(0) is not defined, as the natural logarithm is only defined for positive real numbers. As x approaches 0 from the positive side, ln(x) approaches negative infinity.
-
Q: What is the domain and range of ln(x)?
- A: The domain of ln(x) is all positive real numbers (x > 0), and the range is all real numbers.
Conclusion
The natural logarithm is a fundamental function in mathematics with wide-ranging applications in various fields. Understanding its properties, applications, and relationships with other mathematical concepts is essential for anyone studying these disciplines. From calculus to physics to economics, the natural logarithm provides a powerful tool for modeling and analyzing complex phenomena. By mastering the concepts and techniques discussed in this article, you can gain a deeper understanding of the natural logarithm and its role in the world around us.
How do you think the natural logarithm impacts your field of study or work? Are you interested in exploring other types of logarithmic functions?
Latest Posts
Latest Posts
-
Diagram Of The Autonomic Nervous System
Nov 21, 2025
-
What Are Virtual Functions In C
Nov 21, 2025
-
What Is The Domain Of A Polynomial
Nov 21, 2025
-
Where Did The Glorious Revolution Take Place
Nov 21, 2025
-
How To Address A Letter To A Senator
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Ln X Ln X 1 Ln X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.