Lim 1/x As X Approaches Infinity
pythondeals
Nov 04, 2025 · 9 min read
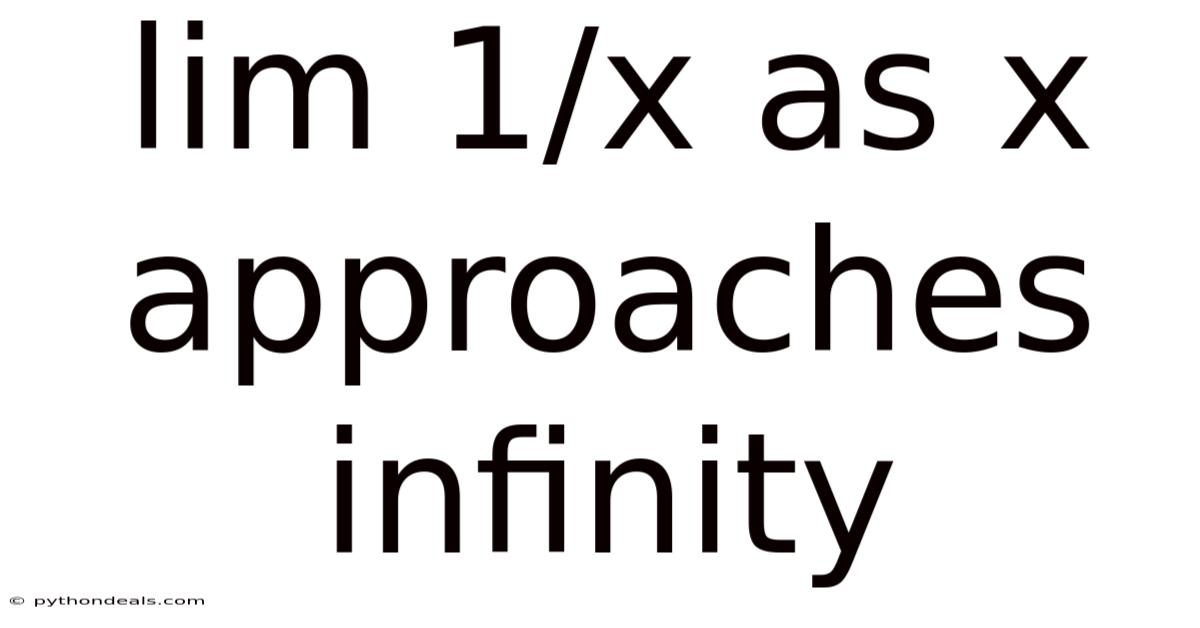
Table of Contents
Let's embark on a journey into the fascinating world of limits, focusing on a specific and fundamental example: the limit of 1/x as x approaches infinity. This seemingly simple expression unlocks a deep understanding of calculus and serves as a building block for more complex concepts. We will explore the intuitive meaning, formal definition, graphical representation, and practical applications of this limit.
Introduction: The Essence of Limits
Before diving into the specifics of lim (1/x) as x approaches infinity, it's crucial to grasp the core concept of a limit. In essence, a limit describes the value that a function "approaches" as its input (variable) gets arbitrarily close to a certain value. This "certain value" can be a finite number, infinity, or even negative infinity. Limits are the foundation of calculus, enabling us to analyze the behavior of functions at points where they might otherwise be undefined or exhibit unusual characteristics. They are instrumental in defining continuity, derivatives, and integrals.
Imagine a runner approaching the finish line of a race. The closer the runner gets to the finish line, the closer their position "approaches" the finish line itself. However, they may never technically reach the finish line at any specific moment (due to the infinitely small steps they take). The finish line is the limit of their position as time goes on. Similarly, in the context of functions, we're concerned with what value the output of a function trends toward as the input changes.
The Limit of 1/x as x Approaches Infinity: An Intuitive Understanding
The expression "lim (1/x) as x approaches infinity" can be written mathematically as:
lim (1/x) x→∞
This notation asks a crucial question: What happens to the value of the fraction 1/x as the value of x becomes incredibly, unbelievably large – approaching infinity?
Think about it practically. If x is 1, 1/x is 1. If x is 10, 1/x is 0.1. If x is 100, 1/x is 0.01. If x is 1000, 1/x is 0.001. As you increase the value of x dramatically, the value of 1/x gets progressively smaller and smaller. It gets closer and closer to zero.
The key is that 1/x never actually reaches zero unless x is truly infinite, which is not a real number. Instead, 1/x gets arbitrarily close to zero as x grows without bound. This is the essence of the limit: it describes the value the function approaches, not necessarily the value it equals.
Therefore, we can intuitively say that:
lim (1/x) = 0 x→∞
A More Formal Definition: Epsilon-Delta
While the intuitive explanation is helpful, mathematics demands rigor. The formal definition of a limit, often referred to as the epsilon-delta definition, provides the necessary precision. For our specific example, it goes like this:
For every ε > 0 (epsilon, a small positive number), there exists an M > 0 (a large positive number) such that if x > M, then |1/x - 0| < ε.
Let's break this down:
-
ε > 0: This means we can choose any arbitrarily small positive number. This number represents the maximum allowable difference between 1/x and our claimed limit (0).
-
M > 0: This means we can find a sufficiently large positive number. This number represents a threshold for x.
-
x > M: This means that if x is greater than our threshold M, then...
-
|1/x - 0| < ε: ...the absolute value of the difference between 1/x and 0 is less than our chosen epsilon. In other words, 1/x is "close enough" to 0.
The definition is essentially saying: No matter how small you want the difference between 1/x and 0 to be (that's your epsilon), I can always find a value M such that if x is larger than M, 1/x will be within that desired small difference of 0.
Why is this important? The epsilon-delta definition provides a proof that the limit is indeed 0. It's not just an observation; it's a mathematically sound argument.
Graphical Representation: Visualizing the Limit
A graph provides a powerful visual aid for understanding this limit. Consider the graph of the function y = 1/x. As you move further to the right along the x-axis (i.e., as x increases towards infinity), the curve gets closer and closer to the x-axis (y = 0).
-
X-axis as Asymptote: The x-axis acts as a horizontal asymptote for the function y = 1/x. An asymptote is a line that a curve approaches but never actually touches (or crosses) as it tends towards infinity or a specific point. In this case, as x approaches infinity, the graph of y = 1/x gets infinitely close to the x-axis, illustrating that the limit is 0.
-
Negative Values: While we're focused on x approaching positive infinity, it's worth noting that as x approaches negative infinity (moving further to the left along the x-axis), the graph of y = 1/x also approaches the x-axis (y = 0). Thus, lim (1/x) as x approaches negative infinity is also 0.
Practical Applications and Implications
The limit of 1/x as x approaches infinity is more than just a theoretical curiosity. It has significant implications in various fields:
-
Calculus: As mentioned earlier, this limit is a fundamental building block for more complex calculus concepts. It helps us understand the behavior of functions, derivatives, and integrals. For example, it's crucial in determining the convergence or divergence of infinite series.
-
Physics: In physics, this concept is used to model situations where a quantity diminishes as another quantity increases without bound. For instance, the gravitational force between two objects decreases as the distance between them increases. As the distance approaches infinity, the gravitational force approaches zero.
-
Engineering: Engineers use limits to analyze the stability of systems. For example, they might examine how the amplitude of oscillations in a circuit changes over time. If the amplitude approaches zero as time approaches infinity, the system is considered stable.
-
Computer Science: In computer science, the concept of limits is applied in the analysis of algorithms. The efficiency of an algorithm is often expressed in terms of its runtime as the input size grows. If the runtime approaches a constant value as the input size approaches infinity, the algorithm is considered to have a good asymptotic complexity.
-
Economics: Economists use limits to model long-term trends and behaviors. For example, they might analyze how the market share of a company changes over time. If the market share approaches a certain value as time approaches infinity, that value represents the company's long-term market position.
Variations and Related Limits
Understanding lim (1/x) as x approaches infinity allows us to tackle related limits more easily:
-
lim (c/x) as x approaches infinity (where c is a constant): The limit is 0. The constant c doesn't change the fundamental behavior. As x grows without bound, c/x will still approach zero.
-
lim (1/x^n) as x approaches infinity (where n is a positive integer): The limit is 0. Raising x to a positive power only makes the denominator grow faster, causing the fraction to approach zero even more quickly.
-
lim (f(x)/g(x)) as x approaches infinity, where f(x) approaches a constant and g(x) approaches infinity: The limit is 0. This is a generalization of the previous examples.
-
Limits with Negative Infinity: lim (1/x) as x approaches negative infinity is also 0. The same reasoning applies. As x becomes a very large negative number, 1/x becomes a very small negative number, approaching zero.
Common Pitfalls and Misconceptions
It's important to avoid these common mistakes:
-
Assuming 1/infinity is equal to 0: Infinity is not a real number; it's a concept. You can't perform arithmetic operations on infinity as you would with regular numbers. It's more accurate to say 1/x approaches 0 as x approaches infinity.
-
Confusing Limits with Actual Values: The limit describes the value the function approaches, not necessarily the value it equals. The function y = 1/x never actually equals 0 for any finite value of x.
-
Ignoring the Epsilon-Delta Definition: While intuition is helpful, relying solely on intuition can lead to errors. The epsilon-delta definition provides the rigorous foundation for proving limits.
Examples and Practice Problems
Let's work through a few examples to solidify your understanding:
Example 1: Find lim (5/x) as x approaches infinity.
Solution: This is a direct application of the concept. As x gets infinitely large, 5/x approaches 0. Therefore, lim (5/x) = 0.
Example 2: Find lim (1/(x^2 + 1)) as x approaches infinity.
Solution: As x approaches infinity, x^2 also approaches infinity. Adding 1 doesn't significantly change that. Therefore, x^2 + 1 approaches infinity. So, we have 1 divided by a very large number, which approaches 0. Thus, lim (1/(x^2 + 1)) = 0.
Example 3: Find lim ((2x + 1) / (x^2 + 3)) as x approaches infinity.
Solution: This one is a bit more complex, but we can use a trick: divide both the numerator and the denominator by the highest power of x in the denominator, which is x^2:
lim ((2x + 1) / (x^2 + 3)) = lim ((2x/x^2 + 1/x^2) / (x^2/x^2 + 3/x^2)) = lim ((2/x + 1/x^2) / (1 + 3/x^2))
As x approaches infinity, 2/x approaches 0, 1/x^2 approaches 0, and 3/x^2 approaches 0. So we have:
lim ((0 + 0) / (1 + 0)) = 0/1 = 0.
Therefore, lim ((2x + 1) / (x^2 + 3)) = 0.
FAQ (Frequently Asked Questions)
-
Q: What does "approaches infinity" really mean?
- A: It means that the value of the variable (x in this case) grows without bound. There is no largest possible value for x.
-
Q: Why is the limit 0 and not just a really small number?
- A: The limit is 0 because we can make 1/x arbitrarily close to 0 by choosing a sufficiently large value for x. There is no lower bound on how close 1/x can get to 0.
-
Q: Is infinity a number?
- A: No, infinity is not a number. It's a concept representing a quantity that grows without bound.
-
Q: What if the limit doesn't exist?
- A: Some functions don't have a limit as x approaches a certain value. For example, the function sin(x) oscillates between -1 and 1 as x approaches infinity and doesn't converge to a specific value.
Conclusion
The limit of 1/x as x approaches infinity is a cornerstone of calculus and a fundamental concept in mathematics. Understanding this limit not only provides insight into the behavior of functions but also lays the groundwork for more advanced mathematical concepts and their applications in diverse fields. By grasping the intuitive meaning, the formal definition, and the graphical representation, you can confidently navigate the world of limits and appreciate their significance. So, go forth and explore the infinite possibilities of calculus!
How has your understanding of limits changed after reading this explanation? Are there any other limit examples you find particularly intriguing?
Latest Posts
Related Post
Thank you for visiting our website which covers about Lim 1/x As X Approaches Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.