Is 7 16 Larger Than 3 8
pythondeals
Dec 01, 2025 · 9 min read
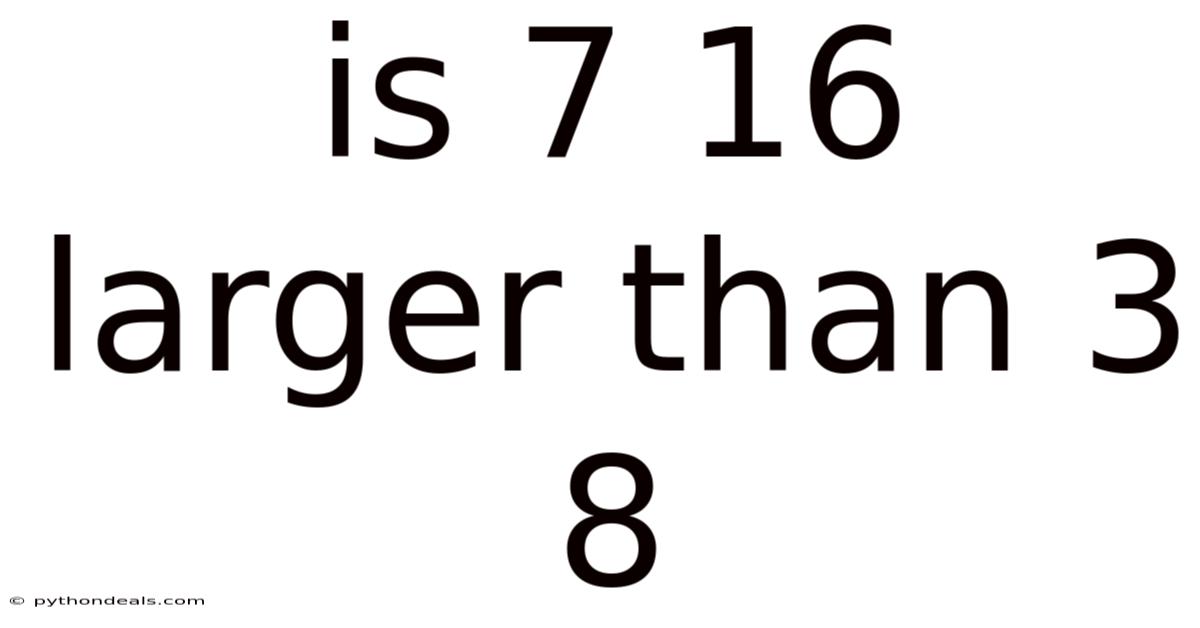
Table of Contents
Navigating the world of fractions can sometimes feel like traversing a mathematical maze. When faced with the question, "Is 7/16 larger than 3/8?", it's natural to pause and consider the best way to compare these two values. Fractions, as representations of parts of a whole, demand careful examination to determine their relative sizes. This article aims to provide a comprehensive guide to understanding and comparing fractions, focusing on the specific comparison between 7/16 and 3/8. We will explore various methods to compare fractions, delve into the mathematical principles behind these methods, and provide practical tips for mastering fraction comparisons.
Understanding Fractions: The Basics
Before diving into the comparison, let's revisit the basics of fractions. A fraction consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts of the whole are being considered, while the denominator represents the total number of equal parts that make up the whole.
For example, in the fraction 7/16, the numerator is 7 and the denominator is 16. This means we are considering 7 parts out of a total of 16 equal parts. Similarly, in the fraction 3/8, the numerator is 3 and the denominator is 8, indicating 3 parts out of 8 equal parts.
Methods for Comparing Fractions
There are several methods to determine which of two fractions is larger. Each method offers a unique approach, and the best choice often depends on the specific fractions being compared and personal preference. Here, we will explore three primary methods:
-
Finding a Common Denominator: This is one of the most reliable and widely used methods for comparing fractions. The idea is to convert the fractions to equivalent fractions with the same denominator. Once the denominators are the same, you can directly compare the numerators; the fraction with the larger numerator is the larger fraction.
-
Cross-Multiplication: This method provides a quick way to compare two fractions without explicitly finding a common denominator. By cross-multiplying the numerators and denominators, you can determine which fraction is larger based on the resulting products.
-
Converting to Decimals: This approach involves converting each fraction to its decimal equivalent. Once in decimal form, the fractions can be easily compared using standard decimal comparison techniques.
Let's delve into each of these methods in detail to illustrate how they can be used to compare 7/16 and 3/8.
Method 1: Finding a Common Denominator
The goal of this method is to rewrite both fractions with the same denominator. To do this, we need to find the least common multiple (LCM) of the denominators. In our case, the denominators are 16 and 8.
-
Finding the LCM of 16 and 8:
The multiples of 8 are: 8, 16, 24, 32, ... The multiples of 16 are: 16, 32, 48, 64, ...
The least common multiple of 8 and 16 is 16.
Now, we need to convert both fractions to have a denominator of 16. The fraction 7/16 already has the desired denominator, so we only need to convert 3/8.
-
Converting 3/8 to an equivalent fraction with a denominator of 16:
To convert 3/8 to an equivalent fraction with a denominator of 16, we need to multiply both the numerator and the denominator by the same number. In this case, we multiply by 2:
(3 * 2) / (8 * 2) = 6/16
Now we have two fractions with the same denominator: 7/16 and 6/16.
-
Comparing the Fractions:
Since both fractions have the same denominator, we can directly compare the numerators:
7/16 compared to 6/16
7 is greater than 6, so 7/16 is greater than 6/16.
Therefore, 7/16 is larger than 3/8.
Method 2: Cross-Multiplication
Cross-multiplication is a shortcut method that allows us to compare fractions without explicitly finding a common denominator. To use this method, we multiply the numerator of the first fraction by the denominator of the second fraction, and the numerator of the second fraction by the denominator of the first fraction.
-
Cross-Multiplying 7/16 and 3/8:
Multiply 7 (numerator of the first fraction) by 8 (denominator of the second fraction): 7 * 8 = 56
Multiply 3 (numerator of the second fraction) by 16 (denominator of the first fraction): 3 * 16 = 48
Now, compare the products:
56 compared to 48
Since 56 is greater than 48, the first fraction (7/16) is larger than the second fraction (3/8).
Therefore, 7/16 is larger than 3/8.
Method 3: Converting to Decimals
This method involves converting each fraction to its decimal equivalent and then comparing the decimal values.
-
Converting 7/16 to a Decimal:
To convert 7/16 to a decimal, divide 7 by 16: 7 ÷ 16 = 0.4375
-
Converting 3/8 to a Decimal:
To convert 3/8 to a decimal, divide 3 by 8: 3 ÷ 8 = 0.375
Now, compare the decimal values:
- 4375 compared to 0.375
Since 0.4375 is greater than 0.375, the first fraction (7/16) is larger than the second fraction (3/8).
Therefore, 7/16 is larger than 3/8.
Practical Tips for Comparing Fractions
Comparing fractions can become easier with practice and a few helpful tips:
-
Simplify Fractions: Before comparing, always check if the fractions can be simplified. Simplifying fractions makes them easier to work with and can sometimes make the comparison more obvious. For example, if you were comparing 4/8 and 1/2, simplifying 4/8 to 1/2 would immediately show that the two fractions are equal.
-
Visualize Fractions: Try to visualize fractions as parts of a whole. For example, think of a pizza cut into equal slices. If you have 7/16 of the pizza, imagine 7 slices out of 16. Comparing this to 3/8, which is 3 slices out of 8, can provide a visual sense of which fraction is larger.
-
Use Benchmarks: Benchmarking fractions against common fractions like 1/2, 1/4, and 3/4 can be helpful. For example, if you know that 7/16 is slightly less than 1/2 and 3/8 is also less than 1/2, you might need to use one of the methods described above to make a more precise comparison. However, benchmarking can give you a quick estimate.
-
Practice Regularly: The more you practice comparing fractions, the more comfortable and efficient you will become. Try working through various examples and using different methods to reinforce your understanding.
Real-World Applications of Fraction Comparison
Understanding how to compare fractions is not just an academic exercise; it has numerous practical applications in everyday life:
-
Cooking and Baking: Recipes often involve fractions, and knowing how to compare them is essential for scaling recipes up or down. For example, if a recipe calls for 3/4 cup of flour and you want to double the recipe, you need to know that doubling 3/4 results in 1 1/2 cups.
-
Shopping and Budgeting: When comparing prices, you might encounter fractions. For example, if one store offers a product for 2/5 off and another offers it for 1/3 off, knowing how to compare these fractions will help you determine which discount is greater.
-
Construction and Measurement: In construction, accurate measurements are critical, and these often involve fractions. Comparing fractions is necessary for cutting materials to the correct size and ensuring that different parts of a project fit together properly.
-
Time Management: Managing time often involves dealing with fractions. For example, if you need to allocate 1/4 of your day to work, 1/8 to exercise, and 1/2 to sleep, understanding how these fractions relate to each other can help you plan your day effectively.
The Mathematical Principles Behind Fraction Comparison
To truly understand why these methods work, let's delve into the mathematical principles behind fraction comparison:
-
Equivalent Fractions: The method of finding a common denominator relies on the concept of equivalent fractions. Equivalent fractions are fractions that have the same value but different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions. The principle is that multiplying both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. This is because you are essentially multiplying the fraction by 1.
-
Properties of Inequalities: When comparing fractions, we are essentially dealing with inequalities. The properties of inequalities state that if a > b and c > 0, then ac > bc. In the context of fractions, this means that if two fractions have the same denominator, the fraction with the larger numerator is larger.
-
Decimal Representation: Converting fractions to decimals allows us to use the properties of real numbers for comparison. Every fraction can be expressed as a decimal, either terminating or repeating. Comparing decimals is straightforward because we can compare the digits in each place value to determine which number is larger.
Common Mistakes to Avoid
When comparing fractions, there are several common mistakes to avoid:
-
Comparing Numerators Directly: A common mistake is to simply compare the numerators without considering the denominators. For example, mistakenly assuming that 3/4 is always larger than 1/2 because 3 is larger than 1. The denominators must be considered to accurately compare the fractions.
-
Incorrectly Finding Common Denominators: Make sure to find the least common multiple (LCM) correctly. Using a common multiple that is not the least common multiple will still work but will require simplifying the fractions later.
-
Arithmetic Errors: Double-check your calculations, especially when converting fractions to decimals or finding equivalent fractions. A simple arithmetic error can lead to an incorrect comparison.
FAQ: Frequently Asked Questions
-
Q: Can I always use cross-multiplication to compare fractions?
- A: Yes, cross-multiplication is a reliable method for comparing fractions, as long as you perform the multiplication correctly and compare the products accurately.
-
Q: Is it always necessary to find the least common denominator?
- A: No, it is not always necessary to find the least common denominator. Any common multiple will work, but using the least common multiple simplifies the process and reduces the need for simplifying fractions later.
-
Q: What if the fractions have negative signs?
- A: If the fractions have negative signs, remember that the more negative a number is, the smaller it is. For example, -1/2 is smaller than -1/4.
Conclusion
In summary, comparing fractions involves understanding the relationship between the numerator and denominator and using appropriate methods to determine their relative sizes. Whether you choose to find a common denominator, use cross-multiplication, or convert to decimals, the key is to apply the methods accurately and understand the mathematical principles behind them. In the case of 7/16 and 3/8, we have shown through multiple methods that 7/16 is indeed larger than 3/8. By mastering these techniques and avoiding common mistakes, you can confidently navigate fraction comparisons in various real-world scenarios.
Now that you've explored these methods, which one do you find the most intuitive and easy to use? And how might you apply this knowledge in your daily life, whether it's in the kitchen, at the store, or managing your time?
Latest Posts
Latest Posts
-
What Type Of Energy Is Mechanical
Dec 01, 2025
-
What Are The Parts Of A Sentence
Dec 01, 2025
-
How Do You Do A Scatter Plot On Excel
Dec 01, 2025
-
Domain Of A Function In Interval Notation
Dec 01, 2025
-
According To Marx Social Conflict Was Caused By
Dec 01, 2025
Related Post
Thank you for visiting our website which covers about Is 7 16 Larger Than 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.