Is 1 2 Larger Than 3 4
pythondeals
Nov 15, 2025 · 10 min read
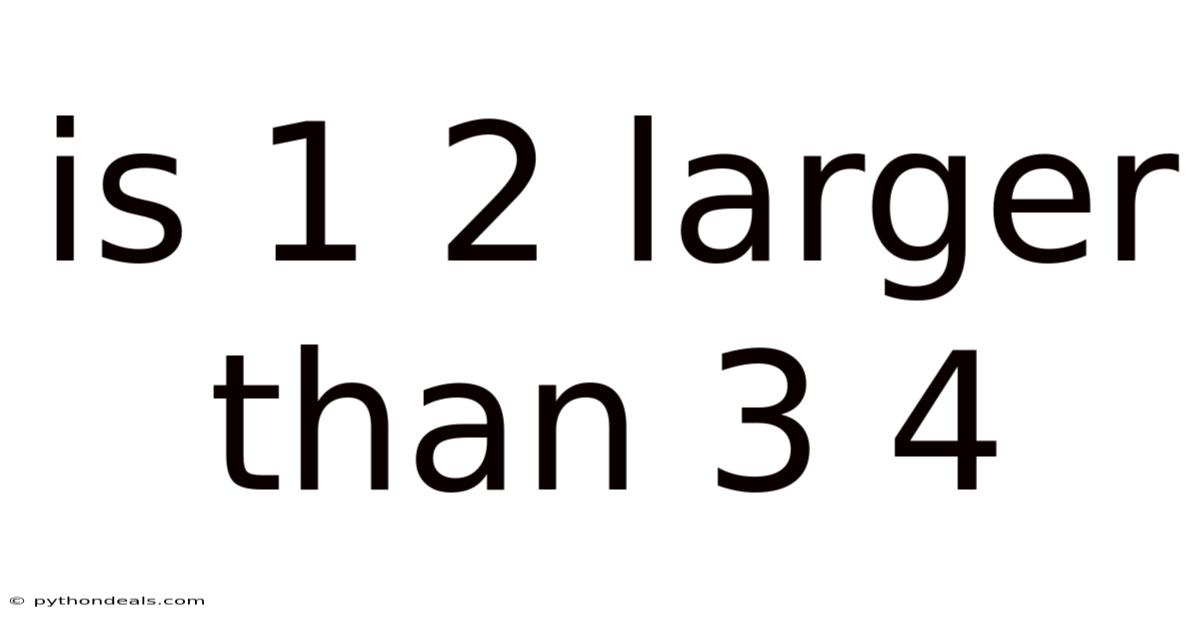
Table of Contents
Navigating the realm of fractions can sometimes feel like traversing a mathematical maze. The simple question, "Is 1/2 larger than 3/4?" often leads to confusion, especially for those who are just beginning their journey into the world of numbers. Understanding how to compare fractions is not merely an academic exercise; it's a fundamental skill that has practical applications in everyday life, from cooking to budgeting.
In this comprehensive guide, we'll explore the depths of fractional comparison. We'll start with the basics, breaking down the anatomy of a fraction and the principles that govern their values. From there, we'll delve into several methods for comparing fractions, including finding common denominators, cross-multiplication, and converting fractions to decimals. Each method will be explained with detailed examples, ensuring you grasp the nuances of each approach. We'll also discuss common pitfalls and misconceptions that can lead to errors in fraction comparison.
As we progress, we'll tackle more complex scenarios, such as comparing mixed numbers and improper fractions. We'll provide real-world examples to illustrate how these concepts are applied in practical situations. By the end of this article, you'll not only be able to confidently determine whether 1/2 is larger than 3/4, but you'll also have a solid foundation for tackling any fractional comparison that comes your way.
Understanding Fractions: The Basics
Before diving into comparing fractions, it's crucial to understand what fractions represent. A fraction is a way of representing a part of a whole. It consists of two main components: the numerator and the denominator.
Numerator: The numerator is the number above the fraction bar, indicating how many parts of the whole you have. Denominator: The denominator is the number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2:
- 1 is the numerator, representing one part.
- 2 is the denominator, representing that the whole is divided into two equal parts.
Similarly, in the fraction 3/4:
- 3 is the numerator, representing three parts.
- 4 is the denominator, representing that the whole is divided into four equal parts.
The size of the denominator is inversely proportional to the size of each part. This means that the larger the denominator, the smaller each individual part is. For instance, if you divide a pizza into 8 slices (denominator of 8), each slice will be smaller than if you divide the same pizza into 4 slices (denominator of 4).
Methods for Comparing Fractions
There are several methods to compare fractions effectively. Each method has its strengths and is suitable for different scenarios. Here are some of the most common and reliable methods:
1. Finding a Common Denominator
One of the most straightforward methods for comparing fractions is to find a common denominator. This involves converting the fractions to equivalent fractions that share the same denominator. Once the denominators are the same, you can simply compare the numerators. The fraction with the larger numerator is the larger fraction.
Steps to Find a Common Denominator:
-
Identify the Denominators: Determine the denominators of the fractions you want to compare. In our case, we want to compare 1/2 and 3/4, so our denominators are 2 and 4.
-
Find the Least Common Multiple (LCM): Determine the least common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly. For 2 and 4, the LCM is 4.
-
Convert the Fractions: Convert each fraction into an equivalent fraction with the LCM as the new denominator. To do this, multiply both the numerator and the denominator of each fraction by the factor that makes the original denominator equal to the LCM.
- For 1/2, we need to multiply both the numerator and the denominator by 2 to get a denominator of 4: (1 * 2) / (2 * 2) = 2/4
- For 3/4, the denominator is already 4, so we don't need to change it.
-
Compare the Numerators: Now that both fractions have the same denominator, compare their numerators. In this case, we are comparing 2/4 and 3/4. The fraction with the larger numerator is the larger fraction.
- Since 3 is greater than 2, 3/4 is larger than 2/4.
- Therefore, 3/4 is larger than 1/2.
2. Cross-Multiplication
Cross-multiplication is a quick and efficient method for comparing two fractions. It involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the results.
Steps for Cross-Multiplication:
- Set Up the Fractions: Write the two fractions you want to compare side by side: 1/2 and 3/4.
- Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and multiply the numerator of the second fraction by the denominator of the first fraction.
- 1 (numerator of the first fraction) * 4 (denominator of the second fraction) = 4
- 3 (numerator of the second fraction) * 2 (denominator of the first fraction) = 6
- Compare the Results: Compare the two products. The fraction that corresponds to the larger product is the larger fraction.
- Since 6 is greater than 4, 3/4 is larger than 1/2.
Cross-multiplication works because it effectively scales both fractions to have a common denominator without explicitly finding the LCM.
3. Converting Fractions to Decimals
Another effective method for comparing fractions is to convert them into decimal form. This can be particularly useful when dealing with fractions that have denominators that are not easily converted to a common denominator.
Steps to Convert Fractions to Decimals:
- Divide the Numerator by the Denominator: Divide the numerator of each fraction by its denominator.
- For 1/2: 1 ÷ 2 = 0.5
- For 3/4: 3 ÷ 4 = 0.75
- Compare the Decimals: Compare the resulting decimal values. The fraction with the larger decimal value is the larger fraction.
- Comparing 0.5 and 0.75, we see that 0.75 is larger than 0.5.
- Therefore, 3/4 is larger than 1/2.
Converting fractions to decimals makes the comparison process straightforward, as decimals are easy to compare at a glance.
Common Pitfalls and Misconceptions
When comparing fractions, it's easy to fall into common traps that can lead to incorrect conclusions. Here are some pitfalls to avoid:
1. Assuming Larger Denominator Means Larger Fraction: A common misconception is that a fraction with a larger denominator is always larger. This is incorrect because the denominator indicates the number of parts the whole is divided into. The larger the denominator, the smaller each individual part is. For example, 1/100 is much smaller than 1/2, even though 100 is much larger than 2.
2. Neglecting to Find a Common Denominator: Trying to compare fractions directly without finding a common denominator can be misleading. For example, it's not immediately obvious which is larger: 5/8 or 7/12. However, by finding a common denominator (24), we can convert these to 15/24 and 14/24, respectively, making it clear that 5/8 is larger.
3. Errors in Cross-Multiplication: Cross-multiplication is a reliable method, but errors can occur if the multiplication is done incorrectly. Always double-check your calculations to ensure accuracy.
4. Misinterpreting Decimal Values: When converting fractions to decimals, make sure to perform the division accurately. A small error in the division can lead to an incorrect comparison.
Comparing Mixed Numbers and Improper Fractions
So far, we've focused on comparing proper fractions (where the numerator is less than the denominator). However, we also need to know how to compare mixed numbers and improper fractions.
Mixed Numbers: A mixed number is a combination of a whole number and a proper fraction, such as 2 1/4. Improper Fractions: An improper fraction is one where the numerator is greater than or equal to the denominator, such as 5/4.
Comparing Mixed Numbers: When comparing mixed numbers, first compare the whole number parts. If the whole number parts are different, the mixed number with the larger whole number is larger. If the whole number parts are the same, then compare the fractional parts using one of the methods discussed earlier (common denominator, cross-multiplication, or decimal conversion).
Example: Compare 3 1/2 and 3 3/4.
- The whole number parts are both 3, so we need to compare the fractional parts: 1/2 and 3/4.
- We already know that 3/4 is larger than 1/2.
- Therefore, 3 3/4 is larger than 3 1/2.
Comparing Improper Fractions: When comparing improper fractions, you can use the same methods as with proper fractions (common denominator, cross-multiplication, or decimal conversion). Alternatively, you can convert the improper fractions to mixed numbers and then compare the mixed numbers.
Example: Compare 5/4 and 7/5.
- Using a common denominator (20):
- 5/4 = 25/20
- 7/5 = 28/20
- Since 28/20 is larger than 25/20, 7/5 is larger than 5/4.
Converting to Mixed Numbers:
- 5/4 = 1 1/4
- 7/5 = 1 2/5
- The whole number parts are both 1, so we compare the fractional parts: 1/4 and 2/5.
- Using a common denominator (20):
- 1/4 = 5/20
- 2/5 = 8/20
- Since 8/20 is larger than 5/20, 2/5 is larger than 1/4.
- Therefore, 7/5 is larger than 5/4.
Real-World Examples
Understanding how to compare fractions is not just a theoretical exercise; it has practical applications in many everyday situations. Here are a few examples:
1. Cooking: Suppose you are following a recipe that calls for 1/3 cup of sugar, but you want to double the recipe. You need to determine if 2/6 cup of sugar is the same as 1/3 cup. By finding a common denominator, you can see that 2/6 is indeed equal to 1/3 (2/6 = 1/3).
2. Budgeting: You want to save 1/4 of your monthly income and spend 3/10 on rent. You need to know which amount is larger to plan your budget effectively. By converting these fractions to decimals (1/4 = 0.25 and 3/10 = 0.3), you can easily see that you spend more on rent than you save.
3. Construction: A carpenter needs to cut a piece of wood that is 5/8 of an inch thick and another piece that is 9/16 of an inch thick. To ensure a proper fit, he needs to know which piece is thicker. By finding a common denominator (16), he can compare 10/16 and 9/16, and see that the 5/8 inch piece is thicker.
Conclusion
Comparing fractions is a fundamental skill with wide-ranging applications. By understanding the basics of fractions and mastering the methods for comparison—finding common denominators, cross-multiplication, and converting to decimals—you can confidently tackle any fractional comparison that comes your way. In the case of 1/2 versus 3/4, we've clearly established that 3/4 is the larger fraction.
Remember to avoid common pitfalls and misconceptions, and to apply these techniques to real-world scenarios to reinforce your understanding. With practice, comparing fractions will become second nature, empowering you to make informed decisions in various aspects of life.
How do you plan to use these techniques in your daily life? Are there any other methods you find helpful for comparing fractions?
Latest Posts
Latest Posts
-
How To Get Axis Of Symmetry
Nov 15, 2025
-
Calling Of Saint Matthew By Caravaggio
Nov 15, 2025
-
When Do You Use Absolute Value In Radicals
Nov 15, 2025
-
How Many Kinds Of Light Are There
Nov 15, 2025
-
What Plants Are Found In The Tropical Rainforest
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Larger Than 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.