Integral Of X Ln X 2
pythondeals
Nov 21, 2025 · 8 min read
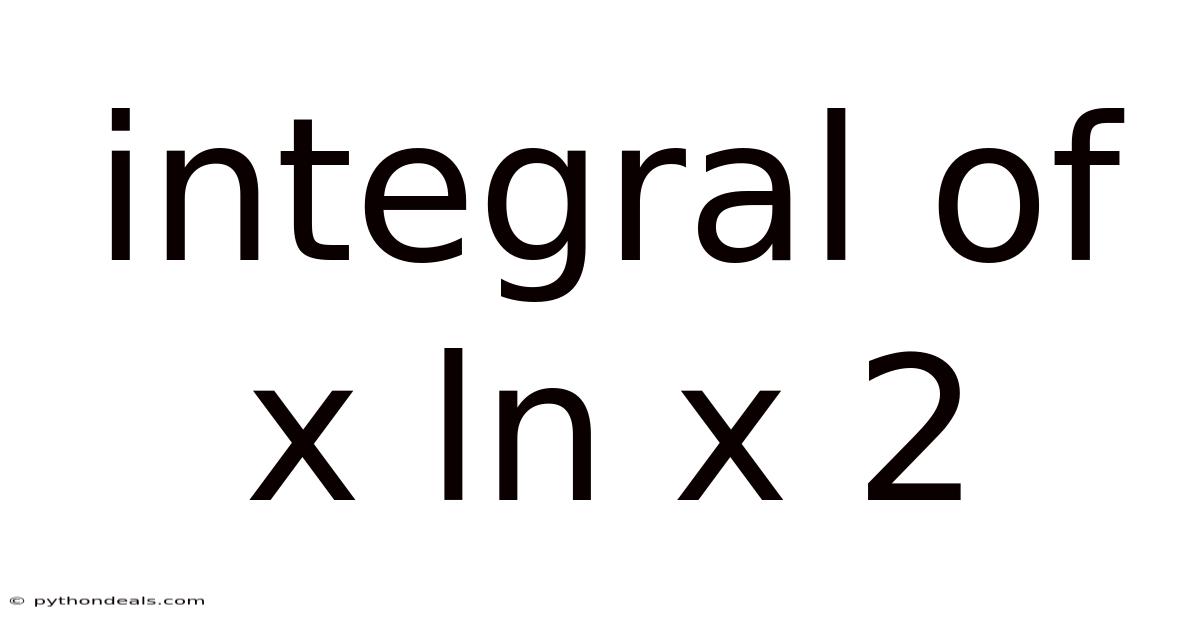
Table of Contents
Alright, let's dive into the integral of x ln x² dx, exploring its solution, underlying principles, and practical applications.
Introduction
The integral of x ln x² dx represents a fascinating problem in calculus, combining algebraic and logarithmic functions. Successfully tackling this integral requires a strategic approach, leveraging integration by parts and a keen understanding of logarithmic properties. This journey will provide a comprehensive exploration of the solution, ensuring you grasp not only the 'how' but also the 'why' behind each step. Understanding this integral builds crucial skills applicable in various fields, from physics and engineering to economics and statistics.
To effectively compute this integral, we'll explore some key techniques and properties of integrals. Integration by parts, a fundamental tool in calculus, will play a pivotal role in simplifying the integral into manageable components. Additionally, familiarity with the properties of logarithms will aid in further simplification and accurate problem-solving.
Breaking Down the Integral: A Step-by-Step Solution
To find the integral of x ln x² dx, we’ll employ integration by parts. This technique is based on the formula:
∫ u dv = uv - ∫ v du
Here’s how we’ll proceed:
Step 1: Simplify the Logarithm
First, recognize that ln x² can be simplified using the power rule of logarithms, which states that ln a^b = b ln a.
ln x² = 2 ln x
Thus, our integral becomes:
∫ x ln x² dx = ∫ x (2 ln x) dx = 2 ∫ x ln x dx
Step 2: Apply Integration by Parts
Now, we’ll apply integration by parts to the integral ∫ x ln x dx.
Let: u = ln x dv = x dx
Then: du = (1/x) dx v = ∫ x dx = (1/2) x²
Using the integration by parts formula:
∫ u dv = uv - ∫ v du
∫ ln x * x dx = (ln x) * (1/2)x² - ∫ (1/2)x² * (1/x) dx
∫ x ln x dx = (1/2) x² ln x - (1/2) ∫ x dx
Step 3: Solve the Remaining Integral
Next, solve the remaining integral ∫ x dx:
∫ x dx = (1/2) x² + C
So, the expression becomes:
∫ x ln x dx = (1/2) x² ln x - (1/2) * (1/2) x² + C
∫ x ln x dx = (1/2) x² ln x - (1/4) x² + C
Step 4: Substitute Back into the Original Equation
Recall that we factored out a 2 earlier. We now need to multiply our result by 2:
2 ∫ x ln x dx = 2 * [(1/2) x² ln x - (1/4) x²] + C
2 ∫ x ln x dx = x² ln x - (1/2) x² + C
Therefore, the integral of x ln x² dx is:
∫ x ln x² dx = x² ln x - (1/2) x² + C
A Comprehensive Overview: Understanding the Underlying Concepts
The integral ∫ x ln x² dx combines both algebraic and logarithmic functions, making its solution a bit more involved than simpler integrals. To fully appreciate the solution, let’s delve into the underlying concepts:
Integration by Parts: Integration by parts is a technique derived from the product rule for differentiation. It’s particularly useful when integrating a product of two functions, one of which simplifies upon differentiation while the other simplifies upon integration.
The formula for integration by parts is:
∫ u dv = uv - ∫ v du
Here, u and v are functions of x, and du and dv are their respective differentials. The key to successfully applying integration by parts lies in the strategic choice of u and dv. A helpful guideline, often referred to as LIATE, can assist in this selection:
L: Logarithmic functions I: Inverse trigonometric functions A: Algebraic functions T: Trigonometric functions E: Exponential functions
The function that appears earlier in the list is generally chosen as u, as it tends to simplify when differentiated.
Logarithmic Properties: Logarithmic properties are essential for simplifying and manipulating logarithmic expressions, making them easier to integrate or differentiate. The key property used in solving ∫ x ln x² dx is the power rule:
ln a^b = b ln a
This property allows us to rewrite ln x² as 2 ln x, which simplifies the integral significantly.
Indefinite Integrals and the Constant of Integration: When finding an indefinite integral, we always include a constant of integration, denoted as C. This is because the derivative of a constant is zero, meaning that when we reverse the process of differentiation (i.e., integration), we lose information about any constant term that might have been present in the original function.
For example, consider the integral ∫ 2x dx. The result is x² + C, where C represents any constant. This means that x², x² + 1, x² - 5, and so on, are all valid antiderivatives of 2x.
Advanced Techniques: Alternative Approaches and Complex Scenarios
While the integration by parts method is effective, there can be variations and more complex scenarios. Here are a few points to consider:
Substitution Method: Although integration by parts is the primary method for ∫ x ln x² dx, sometimes a clever substitution can simplify the problem. However, for this particular integral, substitution alone is not as straightforward as integration by parts.
Definite Integrals: If we were dealing with a definite integral, such as ∫[1 to e] x ln x² dx, we would follow the same steps to find the indefinite integral and then evaluate it at the limits of integration:
∫[1 to e] x ln x² dx = [x² ln x - (1/2) x²] evaluated from 1 to e
= (e² ln e - (1/2) e²) - (1² ln 1 - (1/2) 1²) = (e² - (1/2) e²) - (0 - (1/2)) = (1/2) e² + (1/2)
More Complex Logarithmic Integrals: Integrals involving more complex logarithmic functions might require a combination of techniques. For example, consider ∫ ln(x² + 1) dx. This integral would typically be solved using integration by parts, where u = ln(x² + 1) and dv = dx. However, the resulting integral would require additional steps, possibly including trigonometric substitution.
Real-World Applications: Where This Integral Matters
Understanding integrals like ∫ x ln x² dx isn't just an academic exercise. They have practical applications in various fields:
Physics: In physics, integrals involving logarithmic functions can arise in problems related to entropy, thermodynamics, and electromagnetic theory. For instance, the entropy of an ideal gas involves logarithmic terms, and calculating changes in entropy often requires evaluating integrals of this form.
Engineering: Engineers use integrals to solve problems related to circuit analysis, signal processing, and control systems. Logarithmic functions appear in the analysis of frequency response and stability of systems.
Economics: In economics, logarithmic functions are used to model growth rates, utility functions, and income distribution. Integrals involving logarithmic terms can be used to calculate total utility or cumulative growth over time.
Statistics: In statistics, integrals of logarithmic functions appear in maximum likelihood estimation and information theory. For example, the likelihood function for certain probability distributions involves logarithmic terms, and maximizing the likelihood function requires solving integrals.
Tips & Expert Advice
Double-Check Your Work: Always double-check your work, especially when dealing with integration by parts. Ensure you’ve correctly chosen u and dv and accurately calculated du and v.
Practice Regularly: Practice is key to mastering integration techniques. Work through a variety of problems to build your skills and confidence.
Understand the Theory: Don’t just memorize formulas. Take the time to understand the underlying theory and principles of calculus. This will help you solve problems more effectively and adapt to new challenges.
Use Technology Wisely: Tools like Wolfram Alpha and online integral calculators can be helpful for checking your work or exploring complex integrals, but don’t rely on them exclusively. Develop your own problem-solving skills.
FAQ (Frequently Asked Questions)
Q: What is integration by parts, and when should I use it? A: Integration by parts is a technique used to integrate the product of two functions. It's particularly useful when one function simplifies upon differentiation while the other simplifies upon integration.
Q: How do I choose u and dv in integration by parts? A: Use the LIATE guideline: Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential. Choose the function that appears earlier in the list as u, as it tends to simplify when differentiated.
Q: What is the power rule of logarithms? A: The power rule of logarithms states that ln a^b = b ln a.
Q: Why do we add a constant of integration when finding indefinite integrals? A: The derivative of a constant is zero, so when we reverse the process of differentiation (i.e., integration), we lose information about any constant term that might have been present in the original function.
Conclusion
The integral of x ln x² dx is a compelling example of how calculus combines different types of functions to create intriguing problems. By mastering techniques like integration by parts and understanding logarithmic properties, you can successfully tackle such integrals and apply these skills in various practical contexts. Always remember to double-check your work, practice regularly, and understand the underlying theory to build your expertise in calculus.
How do you feel about this approach to solving complex integrals? Do you find integration by parts to be a valuable technique, and what are some other integrals you'd like to explore?
Latest Posts
Latest Posts
-
How To Determine End Behavior Of A Polynomial
Nov 21, 2025
-
How Do You Square Negative Numbers
Nov 21, 2025
-
Example Of Rate Of Change In Math
Nov 21, 2025
-
How Do You Find The Base Area
Nov 21, 2025
-
Periodic Table Of Elements States Of Matter
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X Ln X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.