Integral Of X Cos X Dx
pythondeals
Dec 05, 2025 · 9 min read
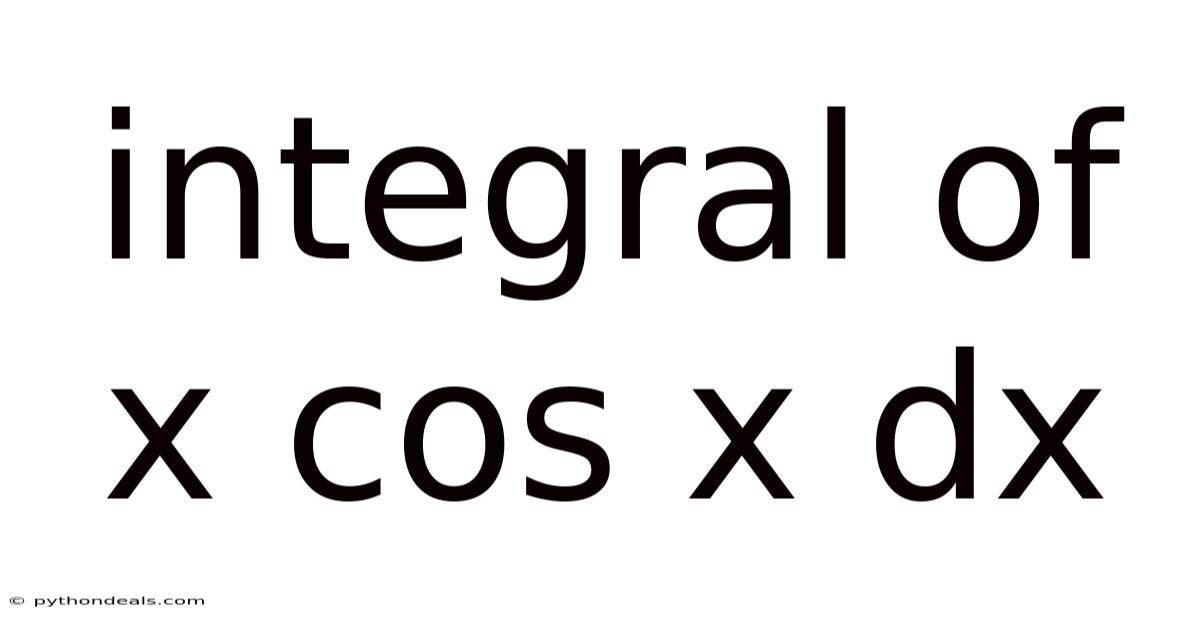
Table of Contents
Navigating the world of calculus can sometimes feel like traversing a complex labyrinth. Among the many tools and techniques available, integration by parts stands out as a particularly powerful method for tackling integrals involving products of functions. One such integral, ∫x cos x dx, perfectly illustrates the elegance and effectiveness of this technique. This article will delve into a comprehensive exploration of how to solve this integral, providing a step-by-step guide, theoretical background, practical tips, and additional insights to ensure a thorough understanding.
Introduction
Calculus, with its two major branches—differentiation and integration—is fundamental to many scientific and engineering disciplines. While differentiation deals with rates of change and slopes of curves, integration concerns accumulation and areas under curves. Integrating a function involves finding another function whose derivative is the original function. However, not all integrals are straightforward, and some require more sophisticated methods.
The integral ∫x cos x dx is a classic example that cannot be solved directly using basic integration rules. Instead, it requires the application of integration by parts, a technique derived from the product rule for differentiation. This method is particularly useful when dealing with integrals of products of functions, where one function becomes simpler upon differentiation and the other upon integration.
Understanding Integration by Parts
Before diving into the solution, it’s crucial to understand the theory behind integration by parts. The formula for integration by parts is derived from the product rule for differentiation.
The Product Rule for Differentiation
The product rule states that if you have two functions, u(x) and v(x), the derivative of their product is:
(uv)' = u'v + uv'
Deriving the Integration by Parts Formula
To derive the integration by parts formula, we start with the product rule and integrate both sides with respect to x:
∫(uv)' dx = ∫(u'v + uv') dx
This simplifies to:
uv = ∫u'v dx + ∫uv' dx
Rearranging the terms, we get the integration by parts formula:
∫uv' dx = uv - ∫u'v dx
In more concise notation, often used for convenience:
∫u dv = uv - ∫v du
Choosing u and dv
The key to successfully applying integration by parts lies in choosing appropriate functions for u and dv. The goal is to select u such that its derivative, du, simplifies the integral, and dv such that it is easily integrable to find v.
A helpful mnemonic device is LIATE, which stands for:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions
- Trigonometric functions
- Exponential functions
This acronym provides a guideline for choosing u. The function that appears earlier in the list is generally a good choice for u.
Step-by-Step Solution of ∫x cos x dx
Now, let’s apply the integration by parts technique to solve ∫x cos x dx.
Step 1: Identify u and dv
Following the LIATE rule, we identify the functions in our integral:
- x is an algebraic function (A)
- cos x is a trigonometric function (T)
Since algebraic functions come before trigonometric functions in the LIATE sequence, we choose:
u = xdv = cos x dx
Step 2: Calculate du and v
Next, we find du and v:
du = dx(the derivative of x with respect to x)v = ∫cos x dx = sin x(the integral of cos x is sin x)
Step 3: Apply the Integration by Parts Formula
Using the formula ∫u dv = uv - ∫v du, we substitute the values we found:
∫x cos x dx = x sin x - ∫sin x dx
Step 4: Evaluate the Remaining Integral
Now we need to evaluate ∫sin x dx, which is a standard integral:
∫sin x dx = -cos x + C
where C is the constant of integration.
Step 5: Final Solution
Substituting this result back into our equation, we get the final solution:
∫x cos x dx = x sin x - (-cos x) + C
Simplifying, we have:
∫x cos x dx = x sin x + cos x + C
Comprehensive Overview
Detailed Explanation
Let's break down the solution step by step to ensure clarity.
-
Initial Setup: The integral ∫x cos x dx presents a product of two functions, x and cos x, making it suitable for integration by parts.
-
Choosing u and dv: Following the LIATE mnemonic, we prioritize algebraic functions over trigonometric functions. Thus, u = x and dv = cos x dx.
-
Calculating du and v: Differentiating u gives du = dx. Integrating dv gives v = sin x. Remember, when finding v, we don't include the constant of integration, as it will be accounted for in the final step.
-
Applying the Formula: The integration by parts formula transforms the original integral into a new one:
∫x cos x dx = x sin x - ∫sin x dxThis step is crucial because it replaces the original integral with one that is easier to solve.
-
Evaluating the New Integral: The integral ∫sin x dx is a basic integral, and its antiderivative is -cos x.
-
Finalizing the Solution: Substituting -cos x back into the equation gives:
∫x cos x dx = x sin x + cos x + CHere, C represents the constant of integration, which is essential in indefinite integrals.
Common Mistakes to Avoid
When applying integration by parts, several common mistakes can lead to incorrect solutions:
- Incorrectly Choosing u and dv: Selecting inappropriate functions for u and dv can complicate the integral rather than simplify it. Always consider the LIATE mnemonic or other strategies to make the right choice.
- Forgetting the Constant of Integration: The constant of integration, C, is a crucial part of the indefinite integral. Forgetting to include it results in an incomplete solution.
- Sign Errors: Pay close attention to the signs, especially when integrating trigonometric functions. For example, the integral of sin x is -cos x, not cos x.
- Incorrectly Applying the Formula: Ensure that you correctly substitute u, v, du, and dv into the integration by parts formula.
Alternative Approaches
While integration by parts is the standard method for solving ∫x cos x dx, understanding why other methods might not work is equally important.
- Direct Integration: Attempting to directly integrate x cos x is not possible because there is no simple antiderivative for this product.
- Substitution: Simple substitution (u-substitution) is not applicable because there is no function and its derivative readily available in the integral.
Integration by parts remains the most efficient and reliable approach for this type of problem.
Tren & Perkembangan Terbaru
Integration by Parts in Modern Applications
Integration by parts is not just a theoretical exercise; it has numerous practical applications in various fields.
- Physics: In physics, integration by parts is used to solve problems in electromagnetism, quantum mechanics, and wave mechanics. For example, calculating the energy of a system or solving differential equations often involves integration by parts.
- Engineering: Engineers use integration by parts in signal processing, control systems, and structural analysis. It helps in analyzing complex systems and designing efficient solutions.
- Economics: Economists use integration by parts in economic modeling, particularly in problems involving discounted cash flows and present value calculations.
- Computer Science: In computer graphics and simulations, integration by parts can be used to optimize calculations and improve the efficiency of algorithms.
Recent Research
Recent research has focused on extending integration by parts to more complex functions and developing algorithms for automated integration. These advancements aim to make integration techniques more accessible and applicable in diverse fields.
- Symbolic Integration Software: Modern computer algebra systems (CAS) like Mathematica and Maple use advanced algorithms to perform symbolic integration, including integration by parts. These tools can handle highly complex integrals that would be difficult or impossible to solve manually.
- Fractional Calculus: Integration by parts has been extended to fractional calculus, which deals with integrals and derivatives of non-integer order. This extension has applications in viscoelasticity, diffusion processes, and control theory.
Tips & Expert Advice
Mastering Integration by Parts
To become proficient in integration by parts, consider the following tips:
- Practice Regularly: The more you practice, the more comfortable you will become with identifying suitable u and dv. Work through a variety of examples to build your skills.
- Use LIATE as a Guide: While LIATE is a useful mnemonic, understand its limitations. Sometimes, swapping the choices for u and dv can lead to a simpler solution.
- Simplify After Each Step: After applying the integration by parts formula, simplify the resulting integral as much as possible before proceeding.
- Check Your Work: Differentiate your final answer to verify that it matches the original integrand. This can help you catch errors and build confidence in your solutions.
- Understand the Theory: Don't just memorize the formula; understand the underlying theory and how it is derived from the product rule. This will help you apply the technique more effectively.
Advanced Techniques
For more challenging integrals, consider these advanced techniques:
- Tabular Integration: Tabular integration, also known as the "tic-tac-toe" method, is a streamlined approach for repeated integration by parts, especially when one function can be differentiated to zero.
- Reduction Formulas: For integrals involving powers of trigonometric functions or other complex expressions, derive reduction formulas to simplify the integration process.
- Complex Integration: In some cases, using complex integration techniques can simplify real integrals. This involves converting the real integral into a complex contour integral and applying the residue theorem.
FAQ (Frequently Asked Questions)
Q: Why can't I use simple u-substitution for ∫x cos x dx? A: Simple u-substitution requires a function and its derivative to be present in the integral. In ∫x cos x dx, while you have cos x, its direct "derivative" (-sin x) isn't explicitly there to allow for a straightforward substitution.
Q: How does LIATE help in choosing u and dv? A: LIATE provides a guideline for prioritizing functions when selecting u. Functions that appear earlier in the list are generally easier to differentiate and simplify the integral.
Q: What if I choose the wrong u and dv? A: If you choose the wrong u and dv, the resulting integral might become more complicated rather than simpler. If this happens, go back and try swapping your choices.
Q: Do I always need to include the constant of integration, C? A: Yes, you always need to include the constant of integration, C, in indefinite integrals. This constant represents the family of functions that have the same derivative.
Q: Can integration by parts be used for definite integrals? A: Yes, integration by parts can be used for definite integrals. In this case, you evaluate the uv term at the limits of integration and subtract the integral of v du over the same limits.
Conclusion
Solving ∫x cos x dx using integration by parts is a fundamental exercise in calculus that showcases the power and elegance of this technique. By carefully selecting u and dv, applying the integration by parts formula, and simplifying the resulting integral, we arrive at the solution: ∫x cos x dx = x sin x + cos x + C.
Understanding the theory behind integration by parts, avoiding common mistakes, and practicing regularly are essential for mastering this technique. Furthermore, recognizing the broader applications of integration by parts in various fields highlights its importance in mathematics, science, and engineering.
How do you feel about tackling similar integration problems now? Are you inspired to explore more complex applications of integration by parts?
Latest Posts
Latest Posts
-
How To Find Domain Of Logs
Dec 05, 2025
-
What Is The Relationship Between Ph And Pka
Dec 05, 2025
-
How Many Atp Molecules Are Produced In Aerobic Respiration
Dec 05, 2025
-
Finding Common Difference In Arithmetic Sequence
Dec 05, 2025
-
What Is The Origin And Insertion Of A Muscle
Dec 05, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X Cos X Dx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.