Integral Of X 2 Ln X
pythondeals
Nov 11, 2025 · 7 min read
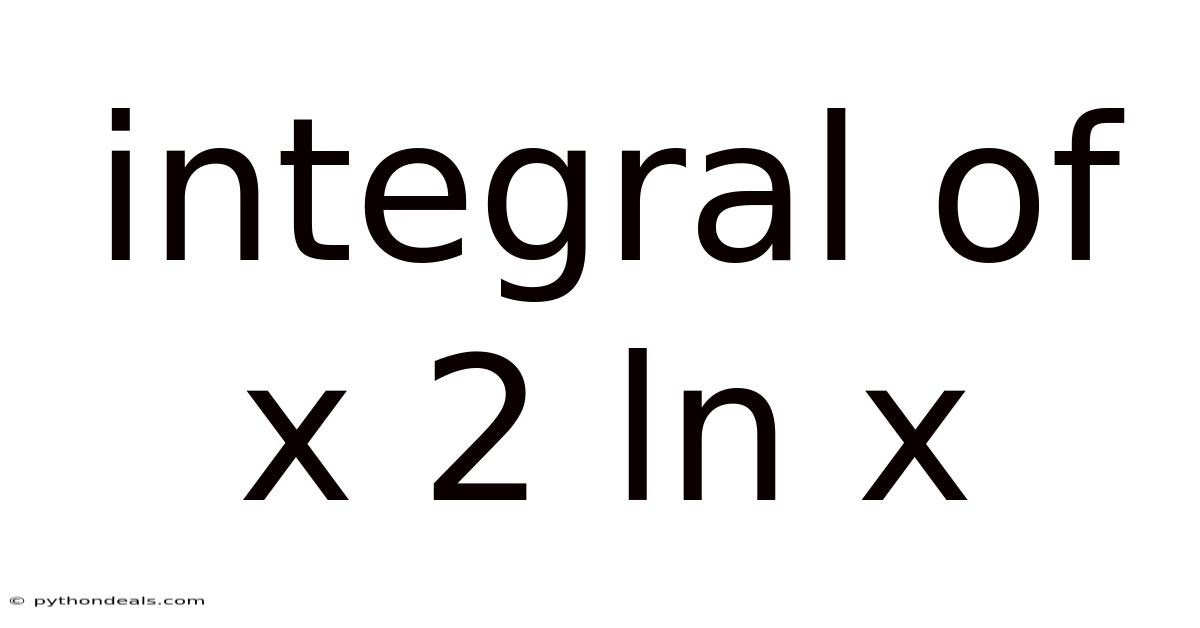
Table of Contents
Navigating the world of calculus can sometimes feel like traversing a dense forest, where each step requires careful planning and a keen understanding of fundamental principles. Among the many techniques and functions you’ll encounter, integration by parts stands out as a versatile tool for tackling integrals involving products of functions. In this comprehensive guide, we’ll explore the integral of x² ln x, a classic example that beautifully illustrates the power and elegance of integration by parts.
Introduction
The integral of x² ln x represents a common yet intriguing problem in calculus, blending a polynomial function (x²) with a logarithmic function (ln x). Solving this integral not only enhances your calculus skills but also deepens your appreciation for how different types of functions interact under integration. Let’s embark on a detailed journey to understand the process, nuances, and practical applications of this integral.
Understanding the Basics
Before diving into the solution, let’s briefly recap some foundational concepts. Integration is the inverse operation of differentiation, and it allows us to find the area under a curve. The indefinite integral, denoted by ∫f(x) dx, represents a family of functions whose derivative is f(x).
Integration by parts is a technique derived from the product rule for differentiation. The formula for integration by parts is:
∫u dv = uv - ∫v du
Where u and v are functions of x, and du and dv are their respective derivatives and integrals. The key to successfully applying integration by parts lies in choosing appropriate functions for u and dv.
Identifying u and dv
The selection of u and dv is crucial for simplifying the integral. A useful guideline is the acronym LIATE, which stands for:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions
- Trigonometric functions
- Exponential functions
This order suggests prioritizing functions higher on the list as u, as their derivatives often simplify the integral.
In the case of ∫x² ln x dx, we have a logarithmic function (ln x) and an algebraic function (x²). According to LIATE, we should choose:
- u = ln x
- dv = x² dx
Now, let's find du and v:
- du = (1/x) dx
- v = ∫x² dx = (x³/3)
Applying Integration by Parts
Using the integration by parts formula, we have:
∫x² ln x dx = (ln x) (x³/3) - ∫(x³/3) (1/x) dx
Simplify the integral:
∫x² ln x dx = (x³ ln x/3) - (1/3) ∫x² dx
Now, integrate x²:
∫x² dx = (x³/3)
Substitute this back into the equation:
∫x² ln x dx = (x³ ln x/3) - (1/3) (x³/3) + C
Finally, simplify to get the result:
∫x² ln x dx = (x³ ln x/3) - (x³/9) + C
Comprehensive Overview: Step-by-Step Breakdown
To ensure a clear understanding, let’s break down the solution into detailed steps.
-
Identify the Functions: Recognize that the integral involves a product of two functions, x² and ln x.
-
Choose u and dv:
- Let u = ln x (logarithmic function)
- Let dv = x² dx (algebraic function)
-
Find du and v:
- Differentiate u to find du: du = (1/x) dx
- Integrate dv to find v: v = ∫x² dx = (x³/3)
-
Apply the Integration by Parts Formula: ∫u dv = uv - ∫v du ∫x² ln x dx = (ln x) (x³/3) - ∫(x³/3) (1/x) dx
-
Simplify the New Integral: ∫x² ln x dx = (x³ ln x/3) - (1/3) ∫x² dx
-
Integrate the Simplified Term: ∫x² dx = (x³/3)
-
Substitute Back and Simplify: ∫x² ln x dx = (x³ ln x/3) - (1/3) (x³/3) + C ∫x² ln x dx = (x³ ln x/3) - (x³/9) + C
-
Final Result: ∫x² ln x dx = (x³/3) (ln x - 1/3) + C
The Importance of the Constant of Integration
It's crucial to include the constant of integration, C, in the final answer. The indefinite integral represents a family of functions, all differing by a constant. Including C acknowledges this family of solutions.
Practical Applications
Understanding how to solve integrals like ∫x² ln x dx has practical applications in various fields, including:
- Physics: Calculating work done by variable forces.
- Engineering: Analyzing stress and strain in materials.
- Economics: Modeling growth rates and economic behavior.
- Statistics: Finding moments and expected values of continuous random variables.
Advanced Techniques and Considerations
While integration by parts is effective for ∫x² ln x dx, there are other advanced techniques that can be used for more complex integrals. These include:
- Tabular Integration: A method that simplifies repeated integration by parts.
- Trigonometric Substitution: Useful for integrals involving square roots of quadratic expressions.
- Partial Fraction Decomposition: Used for integrating rational functions.
Common Mistakes to Avoid
When applying integration by parts, it's easy to make mistakes. Here are some common pitfalls to avoid:
- Incorrectly Choosing u and dv: Follow the LIATE rule to make the best choice.
- Forgetting the Constant of Integration: Always add C to the final result.
- Algebraic Errors: Double-check each step to ensure accuracy.
- Incorrectly Differentiating or Integrating: Review basic differentiation and integration rules.
Tren & Perkembangan Terbaru
In recent years, the integration by parts technique has seen enhanced applications in computational mathematics and symbolic computation software. Modern tools like Mathematica, Maple, and Python libraries (such as SymPy) offer sophisticated capabilities for solving complex integrals, including those requiring multiple iterations of integration by parts. These tools not only provide exact solutions but also aid in visualizing the integration process, making it easier to understand and apply in diverse scientific and engineering contexts.
Furthermore, the ongoing development of AI and machine learning algorithms has opened new avenues for tackling integrals. Neural networks, for example, can be trained to recognize patterns and approximate solutions for integrals that are analytically intractable. This synergy between classical calculus techniques and modern computational methods is shaping the future of mathematical problem-solving.
Tips & Expert Advice
Here are some expert tips to help you master integration by parts:
- Practice Regularly: The more you practice, the more comfortable you'll become with choosing u and dv.
- Use the LIATE Rule: This guideline helps simplify the integral.
- Check Your Work: Always verify your final answer by differentiating it.
- Break Down Complex Integrals: If necessary, break the integral into smaller, more manageable parts.
- Use Symbolic Math Software: Tools like Mathematica or Maple can help check your work and solve complex integrals.
Example: Consider the integral ∫x sin(x) dx. Applying LIATE, we choose u = x and dv = sin(x) dx. Then, du = dx and v = -cos(x). Using integration by parts:
∫x sin(x) dx = -x cos(x) - ∫(-cos(x)) dx ∫x sin(x) dx = -x cos(x) + ∫cos(x) dx ∫x sin(x) dx = -x cos(x) + sin(x) + C
This example showcases how a systematic approach can simplify seemingly complex integrals.
FAQ (Frequently Asked Questions)
Q: What is integration by parts?
A: Integration by parts is a technique used to integrate the product of two functions. It is derived from the product rule for differentiation and is represented by the formula ∫u dv = uv - ∫v du.
Q: How do I choose u and dv?
A: Use the LIATE rule as a guide. Prioritize functions higher on the list as u, as their derivatives often simplify the integral.
Q: What happens if I choose u and dv incorrectly?
A: Choosing u and dv incorrectly can lead to a more complicated integral, or even make the integral unsolvable. Always follow the LIATE rule to minimize this risk.
Q: Why is the constant of integration important?
A: The constant of integration, C, accounts for the family of functions that have the same derivative. Without it, the solution is incomplete.
Q: Can integration by parts be used for definite integrals?
A: Yes, integration by parts can be used for definite integrals. Just remember to evaluate the resulting expression at the limits of integration.
Conclusion
Mastering the integral of x² ln x dx is a significant step in understanding integration by parts. By carefully choosing u and dv, applying the integration by parts formula, and simplifying the resulting expression, you can confidently solve this and similar integrals. Remember to practice regularly, use the LIATE rule, and double-check your work to avoid common mistakes. With these skills, you'll be well-equipped to tackle a wide range of calculus problems and appreciate the beauty and utility of integral calculus.
How do you feel about applying these techniques in your own calculus journey? Are you ready to tackle more complex integrals with confidence?
Latest Posts
Latest Posts
-
How To Find Internal Resistance Of A Battery
Nov 11, 2025
-
What Type Of Bonds Would Be In Co2
Nov 11, 2025
-
What Is The Si Unit For Intensity
Nov 11, 2025
-
Where Does Pyruvate Go After Glycolysis
Nov 11, 2025
-
What Is A Zeroth Order Reaction
Nov 11, 2025
Related Post
Thank you for visiting our website which covers about Integral Of X 2 Ln X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.