Integral Of Sqrt A 2 X 2
pythondeals
Dec 04, 2025 · 9 min read
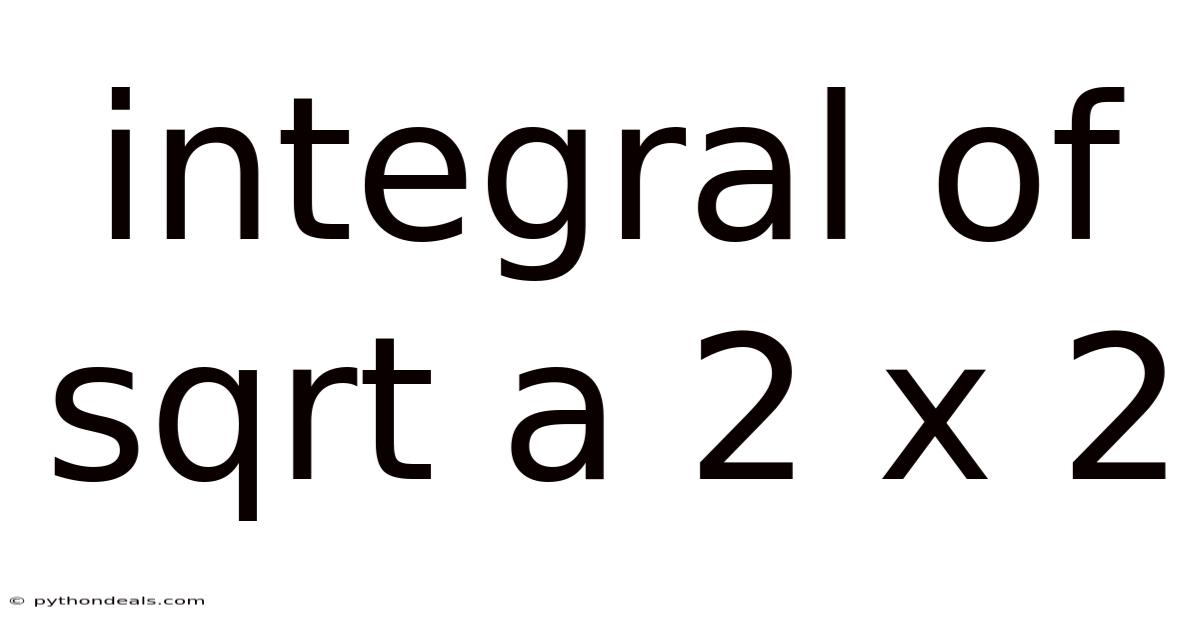
Table of Contents
The integral of √(a² - x²) dx is a classic problem in calculus, often encountered in physics, engineering, and other scientific disciplines. It represents the area under a semicircle with radius a. While the formula itself might seem daunting at first, the steps involved in solving it showcase several fundamental integration techniques, including trigonometric substitution and integration by parts. Understanding this integral provides valuable insights into manipulating complex expressions and applying core calculus principles.
The need to evaluate integrals like √(a² - x²) dx arises frequently when dealing with geometric problems involving circles, ellipses, and other curved shapes. It also appears in the context of physics problems, such as calculating the period of a pendulum or determining the magnetic field produced by certain current configurations. By mastering the solution to this integral, you equip yourself with a powerful tool for tackling a wide range of practical problems.
Breaking Down the Integral: A Step-by-Step Approach
The most common method to solve the integral ∫√(a² - x²) dx involves trigonometric substitution. Here’s a detailed breakdown of each step:
1. Trigonometric Substitution:
The key is to make a substitution that simplifies the square root term. Let’s set:
x = a sin θ
This implies:
dx = a cos θ dθ
The reason for choosing x = a sin θ becomes clear when you substitute it into the original expression:
√(a² - x²) = √(a² - (a sin θ)²) = √(a² - a² sin² θ) = √(a²(1 - sin² θ))
Since 1 - sin² θ = cos² θ, we have:
√(a²(1 - sin² θ)) = √(a² cos² θ) = a cos θ
This substitution effectively removes the square root, making the integral much easier to handle. Remember that this simplification relies on the identity cos² θ = 1 - sin² θ, a cornerstone of trigonometry.
2. Substitute Back into the Integral:
Now, replace x and dx in the original integral with their equivalent expressions in terms of θ:
∫√(a² - x²) dx = ∫(a cos θ)(a cos θ dθ) = a² ∫cos² θ dθ
3. Evaluate the Cosine Squared Integral:
The integral of cos² θ is a standard result, often solved using the double-angle formula. We can rewrite cos² θ as:
cos² θ = (1 + cos 2θ) / 2
Therefore, the integral becomes:
a² ∫cos² θ dθ = a² ∫(1 + cos 2θ) / 2 dθ = (a²/2) ∫(1 + cos 2θ) dθ
Now, we can integrate term by term:
(a²/2) ∫(1 + cos 2θ) dθ = (a²/2) [∫1 dθ + ∫cos 2θ dθ] = (a²/2) [θ + (1/2)sin 2θ] + C
Where C is the constant of integration. The integral of cos 2θ is (1/2)sin 2θ because the derivative of sin 2θ is 2cos 2θ, so we need to divide by 2 to compensate.
4. Convert Back to x:
The final step is to convert the expression back in terms of x. We know that x = a sin θ, which implies:
sin θ = x/a
Therefore,
θ = arcsin(x/a)
We also need to express sin 2θ in terms of x. Using the double-angle formula, sin 2θ = 2 sin θ cos θ. We know sin θ = x/a, but we need to find cos θ. Since cos θ = √(1 - sin² θ), we have:
cos θ = √(1 - (x/a)²) = √(1 - x²/a²) = √( (a² - x²) / a² ) = (1/a)√(a² - x²)
Now we can write sin 2θ in terms of x:
sin 2θ = 2 sin θ cos θ = 2 (x/a) (1/a)√(a² - x²) = (2x/a²) √(a² - x²)
5. Final Solution:
Substituting these expressions back into our result, we get:
(a²/2) [θ + (1/2)sin 2θ] + C = (a²/2) [arcsin(x/a) + (1/2) (2x/a²) √(a² - x²)] + C
Simplifying, we arrive at the final solution:
∫√(a² - x²) dx = (a²/2) arcsin(x/a) + (x/2)√(a² - x²) + C
This formula represents the indefinite integral of √(a² - x²) dx. The constant C signifies that there are infinitely many antiderivatives, each differing by a constant value.
Why Trigonometric Substitution Works: A Deeper Dive
The elegance of trigonometric substitution lies in its ability to transform a complex algebraic expression into a simpler trigonometric form. Specifically, the substitution x = a sin θ leverages the Pythagorean trigonometric identity sin² θ + cos² θ = 1 to eliminate the square root. By choosing x in this way, the expression a² - x² morphs into a²cos² θ, which is easily handled.
Think of the original integral as representing the area under the curve y = √(a² - x²). This curve is actually the upper half of a circle with radius a centered at the origin. The trigonometric substitution essentially parameterizes this circle using the angle θ, allowing us to calculate the area using trigonometric functions, which are much easier to integrate in this context.
Alternative Method: Integration by Parts
While trigonometric substitution is the most common approach, integration by parts can also be used to solve this integral, albeit with slightly more algebraic manipulation. Let's consider:
∫√(a² - x²) dx
We can rewrite this as:
∫1 * √(a² - x²) dx
Now, let's apply integration by parts:
u = √(a² - x²) and dv = dx
Then,
du = (-x / √(a² - x²)) dx and v = x
The integration by parts formula is: ∫u dv = uv - ∫v du
Substituting our values, we get:
∫√(a² - x²) dx = x√(a² - x²) - ∫x * (-x / √(a² - x²)) dx = x√(a² - x²) + ∫x² / √(a² - x²) dx
Now, we need to deal with the new integral, ∫x² / √(a² - x²) dx. We can manipulate this as follows:
∫x² / √(a² - x²) dx = ∫(x² - a² + a²) / √(a² - x²) dx = ∫(x² - a²) / √(a² - x²) dx + ∫a² / √(a² - x²) dx
Notice that (x² - a²) / √(a² - x²) = -√(a² - x²). Therefore:
∫x² / √(a² - x²) dx = -∫√(a² - x²) dx + a² ∫1 / √(a² - x²) dx
Substituting this back into our original equation from integration by parts:
∫√(a² - x²) dx = x√(a² - x²) - ∫x * (-x / √(a² - x²)) dx = x√(a² - x²) + [-∫√(a² - x²) dx + a² ∫1 / √(a² - x²) dx]
∫√(a² - x²) dx = x√(a² - x²) - ∫√(a² - x²) dx + a² ∫1 / √(a² - x²) dx
Now, add ∫√(a² - x²) dx to both sides:
2∫√(a² - x²) dx = x√(a² - x²) + a² ∫1 / √(a² - x²) dx
Finally, divide by 2:
∫√(a² - x²) dx = (x/2)√(a² - x²) + (a²/2) ∫1 / √(a² - x²) dx
The integral ∫1 / √(a² - x²) dx is a standard integral that evaluates to arcsin(x/a). Therefore:
∫√(a² - x²) dx = (x/2)√(a² - x²) + (a²/2) arcsin(x/a) + C
This is the same result we obtained using trigonometric substitution. While integration by parts requires more algebraic manipulation, it demonstrates an alternative route to the solution.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when evaluating this integral. Being aware of them can save you time and frustration:
- Forgetting the Constant of Integration (C): Always remember to add the constant of integration C to the final result of an indefinite integral. This represents the family of all possible antiderivatives.
- Incorrect Trigonometric Substitution: Choosing the wrong substitution can complicate the problem. x = a sin θ is the most effective choice for this specific integral.
- Errors in Trigonometric Identities: Make sure you accurately apply trigonometric identities such as sin² θ + cos² θ = 1 and the double-angle formulas.
- Difficulty Converting Back to x: Carefully convert the trigonometric expressions back to expressions in terms of x. This step requires a solid understanding of inverse trigonometric functions and trigonometric relationships.
- Algebraic Errors in Integration by Parts: Integration by parts involves more algebraic manipulation, increasing the chance of making a mistake. Double-check each step carefully.
Real-World Applications
The integral of √(a² - x²) dx finds applications in various fields:
- Area of a Circle or Ellipse: As mentioned earlier, this integral directly relates to finding the area of a circle or an ellipse. By evaluating the definite integral over a specific interval, you can determine the area of a segment or sector of these shapes.
- Physics: Period of a Pendulum: The period of a simple pendulum involves an integral that can be simplified to the form ∫√(a² - x²) dx, especially when dealing with large-angle oscillations.
- Engineering: Structural Analysis: Integrals of this form can appear in calculations related to stress and strain in structural components, particularly those with circular or elliptical cross-sections.
- Probability and Statistics: The normal distribution, a fundamental concept in statistics, involves integrals that are related to the integral of √(a² - x²) dx.
- Navigation and Cartography: Calculating distances along curved paths, such as those encountered in navigation or mapmaking, can sometimes involve this type of integral.
Frequently Asked Questions (FAQ)
Q: Why use trigonometric substitution instead of direct integration?
A: The function √(a² - x²) doesn't have a straightforward antiderivative that can be found using basic integration rules. Trigonometric substitution transforms the expression into a form that is easier to integrate using trigonometric identities.
Q: Can I use x = a cos θ as a substitution instead of x = a sin θ?
A: Yes, you can use x = a cos θ. The process will be very similar, but you'll be working with sine functions instead of cosine functions. The final result will be mathematically equivalent, although it might look slightly different due to trigonometric identities.
Q: What if the integral was ∫√(x² - a²) dx instead?
A: If the integral is ∫√(x² - a²) dx, you would use a different trigonometric substitution: x = a sec θ. This substitution utilizes the trigonometric identity sec² θ - 1 = tan² θ.
Q: Is there a geometrical interpretation of the constant of integration C?
A: Geometrically, the constant of integration represents a vertical shift of the area function. Since the derivative of a constant is zero, adding a constant to the antiderivative doesn't change its derivative.
Q: How does the value of a affect the integral?
A: The value of a determines the radius of the circle (or the semi-major axis of the ellipse) represented by the function √(a² - x²). A larger value of a corresponds to a larger area under the curve.
Conclusion
The integral of √(a² - x²) dx is a fundamental problem in calculus that demonstrates the power of trigonometric substitution and integration by parts. Understanding the steps involved in solving this integral not only provides a concrete solution but also reinforces key calculus concepts and techniques. From calculating areas of circles to modeling physical phenomena, this integral finds numerous applications across various scientific and engineering disciplines.
By mastering the techniques presented in this article and being mindful of common pitfalls, you can confidently tackle similar integration problems and gain a deeper appreciation for the beauty and utility of calculus. What other integration techniques do you find particularly challenging, and how can we further explore them? Are you now more confident in tackling other integrals involving square roots?
Latest Posts
Latest Posts
-
What Elements Does Carbon Bond With
Dec 04, 2025
-
When To Use Independent Sample T Test
Dec 04, 2025
-
Blood In The Inferior Mesenteric Artery Travels To What Organs
Dec 04, 2025
-
Which Step In The Figure Contains Compact Bone
Dec 04, 2025
-
Does Hf Have Dipole Dipole Forces
Dec 04, 2025
Related Post
Thank you for visiting our website which covers about Integral Of Sqrt A 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.