Integral Of Sin 2x X 2
pythondeals
Dec 01, 2025 · 9 min read
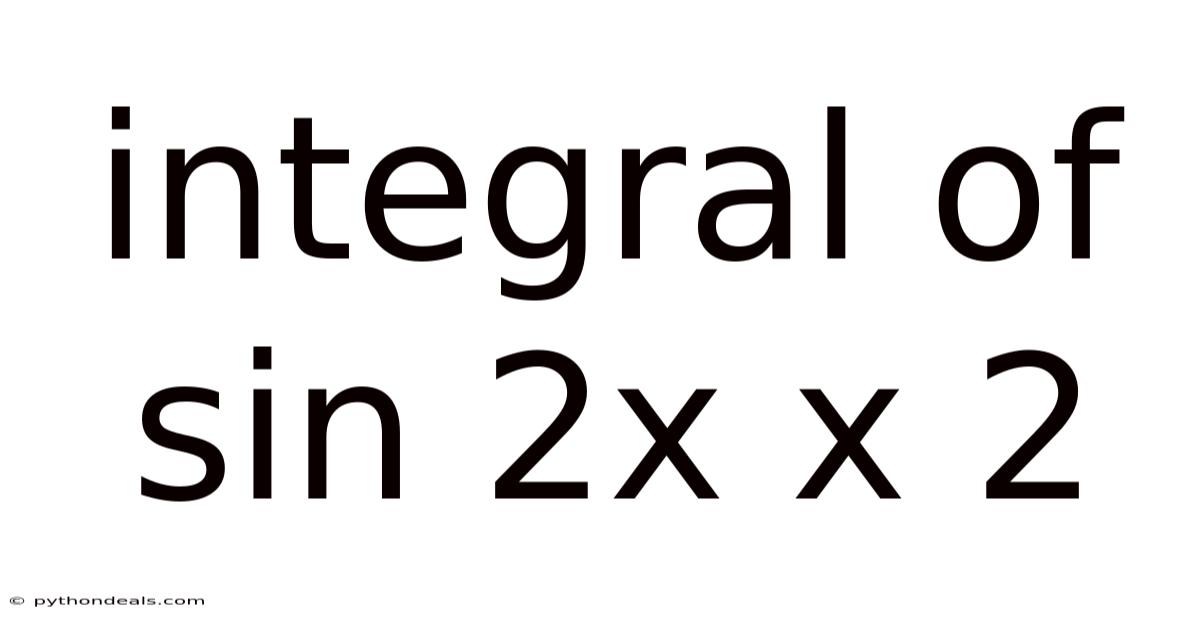
Table of Contents
Navigating the world of calculus can often feel like traversing a complex maze, especially when dealing with integrals involving trigonometric functions and polynomials. One such challenging yet intriguing problem is finding the integral of sin(2x) * x^2. This article offers a detailed, step-by-step guide to solving this integral, complete with explanations and expert tips to help you master this concept. Whether you're a student, an engineer, or simply a math enthusiast, understanding this integral will undoubtedly enhance your calculus skills.
Introduction
The integral of sin(2x) * x^2, often denoted as ∫sin(2x) * x^2 dx, combines trigonometric and polynomial functions, making it a perfect candidate for integration by parts. Integration by parts is a technique derived from the product rule of differentiation and is especially useful when dealing with integrals involving products of functions. The technique simplifies the integral by breaking it into more manageable parts.
In this article, we will delve deep into the process of solving this integral, providing a comprehensive overview, the necessary steps, and expert advice to ensure a clear understanding.
Comprehensive Overview: Integration by Parts
Before diving into the solution, it's essential to understand the method we'll be using: integration by parts. Integration by parts is based on the formula:
∫u dv = uv - ∫v du
Where:
- u is a function that we choose to differentiate.
- dv is a function that we choose to integrate.
- du is the derivative of u.
- v is the integral of dv.
The key to successfully applying integration by parts lies in choosing appropriate functions for u and dv. A common strategy is to choose u as the function that simplifies when differentiated, and dv as the function that is easy to integrate.
Step-by-Step Solution: Integral of sin(2x) * x^2
Step 1: First Application of Integration by Parts
Let's identify our u and dv. In the case of ∫sin(2x) * x^2 dx, it makes sense to choose:
- u = x^2
- dv = sin(2x) dx
Now, we find du and v:
- du = 2x dx
- v = ∫sin(2x) dx = -1/2 * cos(2x)
Using the integration by parts formula: ∫x^2 * sin(2x) dx = x^2 * (-1/2 * cos(2x)) - ∫(-1/2 * cos(2x)) * 2x dx = -1/2 * x^2 * cos(2x) + ∫x * cos(2x) dx
Step 2: Second Application of Integration by Parts
We still have an integral to solve: ∫x * cos(2x) dx. We apply integration by parts again:
- u = x
- dv = cos(2x) dx
Find du and v:
- du = dx
- v = ∫cos(2x) dx = 1/2 * sin(2x)
Applying the integration by parts formula: ∫x * cos(2x) dx = x * (1/2 * sin(2x)) - ∫(1/2 * sin(2x)) dx = 1/2 * x * sin(2x) - 1/2 * ∫sin(2x) dx = 1/2 * x * sin(2x) - 1/2 * (-1/2 * cos(2x)) = 1/2 * x * sin(2x) + 1/4 * cos(2x)
Step 3: Combine the Results
Now, we substitute the result from Step 2 back into the equation from Step 1: ∫x^2 * sin(2x) dx = -1/2 * x^2 * cos(2x) + [1/2 * x * sin(2x) + 1/4 * cos(2x)] = -1/2 * x^2 * cos(2x) + 1/2 * x * sin(2x) + 1/4 * cos(2x) + C
Therefore, the integral of sin(2x) * x^2 is: ∫sin(2x) * x^2 dx = -1/2 * x^2 * cos(2x) + 1/2 * x * sin(2x) + 1/4 * cos(2x) + C
Explanation of Each Step
Detailed Breakdown of Step 1
In Step 1, we identified u and dv as x^2 and sin(2x) dx, respectively. This choice is crucial because differentiating x^2 simplifies the term, reducing its power and making the subsequent integral easier to solve. When we found v by integrating sin(2x) dx, we obtained -1/2 * cos(2x). The application of the integration by parts formula yielded:
∫x^2 * sin(2x) dx = -1/2 * x^2 * cos(2x) + ∫x * cos(2x) dx
Here, the new integral ∫x * cos(2x) dx is simpler than the original, but it still requires another application of integration by parts.
Detailed Breakdown of Step 2
In Step 2, we focused on solving ∫x * cos(2x) dx. Again, we chose u = x and dv = cos(2x) dx. Differentiating u gives du = dx, further simplifying the integral. Integrating dv yields v = 1/2 * sin(2x). Applying integration by parts again:
∫x * cos(2x) dx = 1/2 * x * sin(2x) - ∫(1/2 * sin(2x)) dx = 1/2 * x * sin(2x) + 1/4 * cos(2x)
This step completes the integration process for the remaining part, resulting in a straightforward expression involving sine and cosine functions.
Detailed Breakdown of Step 3
Step 3 involves combining the results from the previous steps. We substitute the solution of ∫x * cos(2x) dx back into the equation from Step 1:
∫x^2 * sin(2x) dx = -1/2 * x^2 * cos(2x) + [1/2 * x * sin(2x) + 1/4 * cos(2x)] = -1/2 * x^2 * cos(2x) + 1/2 * x * sin(2x) + 1/4 * cos(2x) + C
The "+ C" is added to represent the constant of integration, which is always necessary when finding indefinite integrals.
Common Mistakes and How to Avoid Them
Incorrect Choice of u and dv
One of the most common mistakes is choosing the wrong functions for u and dv. The wrong choice can lead to a more complex integral instead of simplifying it. Always aim to choose u such that its derivative is simpler than itself.
How to avoid: Use the acronym LIATE to guide your choice:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (like polynomials)
- Trigonometric functions
- Exponential functions
The function that appears earlier in the list should generally be chosen as u.
Sign Errors
Sign errors are common when integrating trigonometric functions. For example, the integral of sin(2x) is -1/2 * cos(2x), not 1/2 * cos(2x).
How to avoid: Double-check your integration and differentiation, paying close attention to the signs.
Forgetting the Constant of Integration
Forgetting to add the constant of integration (+ C) in indefinite integrals is a frequent mistake.
How to avoid: Always remember to add "+ C" to the final answer of any indefinite integral.
Incorrect Application of the Integration by Parts Formula
Misapplying the integration by parts formula can lead to incorrect results.
How to avoid: Write down the formula explicitly before applying it, and double-check each term.
Advanced Techniques and Extensions
Using Tabular Integration
Tabular integration (also known as the "Tic-Tac-Toe" method) is an alternative approach for repeated integration by parts. It involves creating a table with three columns:
- Sign: Alternating signs (+, -, +, -...).
- u and its Derivatives: The function u and its successive derivatives until you reach zero.
- dv and its Integrals: The function dv and its successive integrals.
Multiply diagonally and sum the results to obtain the integral.
Definite Integrals
If the integral is a definite integral, you'll need to evaluate the result at the upper and lower limits of integration. For example:
∫[0 to π/2] sin(2x) * x^2 dx = [-1/2 * x^2 * cos(2x) + 1/2 * x * sin(2x) + 1/4 * cos(2x)] evaluated from 0 to π/2
Complex Numbers
Complex numbers can sometimes simplify integration problems. Using Euler's formula (e^(ix) = cos(x) + i sin(x)), you can express trigonometric functions in terms of complex exponentials, which can be easier to integrate.
Real-World Applications
Understanding how to solve integrals like ∫sin(2x) * x^2 dx is not just an academic exercise. These techniques are used in various fields:
Engineering
In electrical engineering, such integrals appear when analyzing AC circuits and signal processing. They help in determining the root mean square (RMS) values of signals and power calculations.
Physics
In physics, these integrals can be used in quantum mechanics to calculate probabilities and expectation values, particularly when dealing with wave functions that involve trigonometric and polynomial terms.
Computer Science
In computer graphics and simulations, understanding integrals is crucial for rendering realistic images and simulating physical phenomena.
Expert Advice
Practice Regularly
The key to mastering integration techniques is practice. Work through a variety of problems to build your skills and intuition.
Understand the Theory
Don't just memorize formulas; understand the underlying theory. This will help you apply the techniques more effectively and adapt them to new problems.
Use Online Resources
Take advantage of online resources such as Wolfram Alpha, Khan Academy, and MIT OpenCourseware to supplement your learning.
Seek Help When Needed
Don't hesitate to ask for help from teachers, tutors, or online forums if you're struggling with a particular concept.
FAQ (Frequently Asked Questions)
Q: Why do we use integration by parts? A: Integration by parts is used to integrate products of functions. It breaks down a complex integral into simpler parts that are easier to solve.
Q: How do I choose u and dv? A: Use the LIATE rule to guide your choice. Choose u as the function that becomes simpler when differentiated, and dv as the function that is easy to integrate.
Q: What if I choose the wrong u and dv? A: If you choose the wrong u and dv, you might end up with a more complex integral. Try switching your choices.
Q: Can I use tabular integration for this problem? A: Yes, tabular integration can be used for this problem, especially for repeated integration by parts.
Q: How do I handle definite integrals? A: Solve the indefinite integral first, then evaluate the result at the upper and lower limits of integration.
Q: What is the constant of integration? A: The constant of integration (+ C) is a term added to the result of an indefinite integral to represent the family of functions that have the same derivative.
Conclusion
Solving the integral of sin(2x) * x^2 involves a meticulous application of integration by parts. By breaking down the problem into manageable steps and understanding the underlying theory, you can master this technique and apply it to a wide range of calculus problems. Remember to choose your u and dv wisely, avoid common mistakes, and practice regularly to build your skills.
Calculus is a journey, and every integral you solve is a step forward. Keep exploring, keep learning, and keep pushing your boundaries. How will you apply this knowledge to your next calculus challenge? Are you ready to tackle more complex integrals?
Latest Posts
Latest Posts
-
Why Is Language Important To A Culture
Dec 01, 2025
-
Effects Of The Industrial Revolution On The Environment
Dec 01, 2025
-
Are Dividends Payable A Current Liability
Dec 01, 2025
-
Why Gravitational Potential Energy Is Negative
Dec 01, 2025
-
How To Calculate Mad In Math
Dec 01, 2025
Related Post
Thank you for visiting our website which covers about Integral Of Sin 2x X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.