Half Of 1 1 2 In Fraction
pythondeals
Dec 06, 2025 · 10 min read
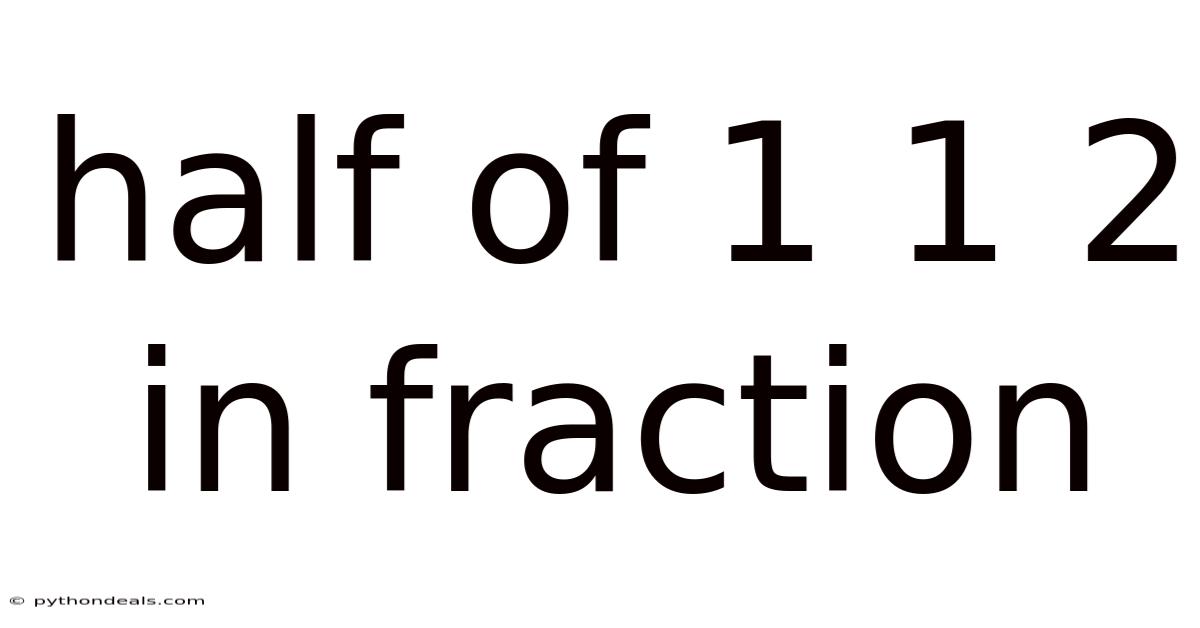
Table of Contents
The world of fractions can sometimes feel like a mathematical maze, especially when you encounter mixed numbers and compound fractions. You might find yourself scratching your head when asked to find half of 1 1/2. But don't worry! This seemingly complex problem is actually quite straightforward once you break it down into simpler steps. This article will guide you through the process of calculating half of 1 1/2 using various methods, ensuring you understand the logic behind each step. We'll explore the basics of fractions, delve into converting mixed numbers to improper fractions, and ultimately conquer the challenge of finding half of 1 1/2. So, buckle up and prepare to unravel the mystery of fractions!
Understanding the Basics of Fractions
Before diving into the specific problem of finding half of 1 1/2, it's crucial to have a solid grasp of the fundamentals of fractions. A fraction represents a part of a whole. It's written as two numbers separated by a line: the numerator (the top number) and the denominator (the bottom number).
- The numerator indicates how many parts of the whole you have.
- The denominator indicates the total number of equal parts that make up the whole.
For example, in the fraction 1/4, the numerator (1) tells us we have one part, and the denominator (4) tells us that the whole is divided into four equal parts.
Fractions can be classified into different types:
- Proper fractions: The numerator is smaller than the denominator (e.g., 1/2, 3/4, 5/8).
- Improper fractions: The numerator is greater than or equal to the denominator (e.g., 3/2, 5/4, 8/8). Improper fractions represent a quantity that is equal to or greater than one whole.
- Mixed numbers: A combination of a whole number and a proper fraction (e.g., 1 1/2, 2 1/4, 3 5/8).
Converting Mixed Numbers to Improper Fractions
The mixed number 1 1/2 represents one whole and one-half. To perform calculations with mixed numbers, it's often easier to convert them into improper fractions. Here's how to do it:
- Multiply the whole number by the denominator of the fraction: In this case, 1 (whole number) * 2 (denominator) = 2.
- Add the result to the numerator of the fraction: 2 + 1 (numerator) = 3.
- Keep the same denominator: The denominator remains 2.
Therefore, 1 1/2 is equivalent to the improper fraction 3/2. This means that one and a half is the same as having three halves.
Finding Half of a Fraction
Now that we've established the basics, let's address the core problem: finding half of 1 1/2. This can be interpreted as multiplying 1 1/2 by 1/2. We can approach this in a couple of ways:
Method 1: Converting to Improper Fractions and Multiplying
This is generally the most straightforward method.
- Convert the mixed number to an improper fraction: We've already done this: 1 1/2 = 3/2.
- Multiply the improper fraction by 1/2: (3/2) * (1/2).
- Multiply the numerators: 3 * 1 = 3.
- Multiply the denominators: 2 * 2 = 4.
- The result is 3/4. Therefore, half of 1 1/2 is 3/4.
Method 2: Visual Representation
Sometimes, visualizing the problem can help solidify your understanding.
- Imagine you have 1 1/2 pizzas. This means you have one whole pizza and half of another pizza.
- You want to find half of what you have. So, you need to divide both the whole pizza and the half pizza into two equal parts.
- Half of the whole pizza is simply 1/2 of a pizza.
- Half of the half pizza is 1/4 of a pizza (because half of one-half is one-quarter).
- Adding these together, you have 1/2 (from the whole pizza) + 1/4 (from the half pizza).
- To add these fractions, you need a common denominator, which is 4. So, 1/2 becomes 2/4.
- Now you have 2/4 + 1/4 = 3/4. This confirms that half of 1 1/2 is 3/4.
Method 3: Distributive Property (Slightly More Advanced)
This method utilizes the distributive property of multiplication.
- Think of 1 1/2 as (1 + 1/2).
- We want to find 1/2 of (1 + 1/2).
- Using the distributive property, we can write this as (1/2 * 1) + (1/2 * 1/2).
- 1/2 * 1 = 1/2.
- 1/2 * 1/2 = 1/4.
- So, we have 1/2 + 1/4.
- As before, we need a common denominator to add these fractions. 1/2 becomes 2/4.
- 2/4 + 1/4 = 3/4. Therefore, half of 1 1/2 is 3/4.
Why is Understanding Fractions Important?
Fractions are a fundamental concept in mathematics with applications in countless real-world scenarios. Here are just a few examples:
- Cooking and Baking: Recipes often use fractional amounts of ingredients (e.g., 1/2 cup of flour, 1/4 teaspoon of salt).
- Measurement: Units of length, weight, and volume are frequently expressed as fractions (e.g., 2 1/2 inches, 3/4 pound).
- Finance: Understanding fractions is crucial for calculating interest rates, discounts, and investment returns.
- Construction and Engineering: Fractions are essential for accurate measurements and calculations in building and design projects.
- Time: We often use fractions of an hour or a minute (e.g., a quarter past the hour, half an hour).
Comprehensive Overview of Related Concepts
To further solidify your understanding, let's explore some related concepts that build upon the foundation of fractions.
- Equivalent Fractions: These are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2, 2/4, and 4/8 are all equivalent fractions. To find equivalent fractions, you can multiply or divide both the numerator and denominator by the same non-zero number.
- Simplifying Fractions: This involves reducing a fraction to its simplest form by dividing both the numerator and denominator by their greatest common factor (GCF). For example, the GCF of 4 and 8 is 4. Dividing both by 4, we get 4/8 = 1/2.
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with that common denominator. Then, you can add or subtract the numerators and keep the same denominator.
- Dividing Fractions: To divide fractions, you invert the second fraction (the divisor) and multiply. For example, (1/2) / (1/4) becomes (1/2) * (4/1) = 4/2 = 2.
- Decimals and Fractions: Decimals and fractions are two different ways of representing the same values. You can convert fractions to decimals by dividing the numerator by the denominator. For example, 1/4 = 0.25. You can convert some decimals to fractions by expressing them as a fraction with a denominator of 10, 100, 1000, etc., and then simplifying. For example, 0.75 = 75/100 = 3/4.
- Percentages and Fractions: Percentages are a way of expressing a number as a fraction of 100. To convert a fraction to a percentage, multiply it by 100. For example, 1/2 = (1/2) * 100 = 50%. To convert a percentage to a fraction, divide it by 100. For example, 25% = 25/100 = 1/4.
Tren & Perkembangan Terbaru
While the fundamental principles of fractions remain constant, there are evolving trends in how they are taught and applied. One notable trend is the increasing emphasis on conceptual understanding over rote memorization. Educators are focusing on helping students develop a deep understanding of what fractions represent and how they relate to real-world situations. This approach encourages critical thinking and problem-solving skills, rather than simply memorizing rules and procedures.
Another trend is the integration of technology into fraction instruction. Interactive simulations, online games, and educational apps are being used to make learning fractions more engaging and accessible. These tools can provide students with visual representations of fractions, immediate feedback on their work, and opportunities to practice independently.
Furthermore, there's growing recognition of the importance of addressing learning gaps in fractions. Many students struggle with fractions because they haven't mastered the underlying concepts. Educators are implementing strategies to identify and address these gaps early on, providing targeted support to students who need it. This often involves revisiting foundational concepts and providing opportunities for hands-on learning and practice. For example, using manipulatives like fraction bars or pie pieces can help students visualize and understand fractional relationships.
Tips & Expert Advice
Here are some tips and expert advice to help you master fractions:
- Start with the Basics: Ensure you have a solid understanding of the basic concepts of fractions, including numerators, denominators, and equivalent fractions. Don't rush ahead until you've mastered these fundamentals.
- Visualize Fractions: Use visual aids such as diagrams, drawings, and manipulatives to help you understand fractions. This can make abstract concepts more concrete and easier to grasp.
- Practice Regularly: The more you practice working with fractions, the more confident and proficient you'll become. Dedicate time each day or week to practice fraction problems.
- Break Down Complex Problems: When faced with a complex fraction problem, break it down into smaller, more manageable steps. This will make the problem less intimidating and easier to solve.
- Check Your Work: Always check your work to ensure that you've made no errors. This is especially important when adding, subtracting, multiplying, and dividing fractions.
- Relate to Real-World Examples: Look for opportunities to apply your knowledge of fractions to real-world situations. This will help you see the relevance of fractions and make them more meaningful.
- Don't Be Afraid to Ask for Help: If you're struggling with fractions, don't be afraid to ask for help from a teacher, tutor, or friend. There are many resources available to support your learning.
- Use Online Resources: There are numerous online resources available to help you learn about fractions, including tutorials, practice problems, and interactive games. Khan Academy, for instance, offers a comprehensive collection of free math lessons, including extensive coverage of fractions.
- Focus on Conceptual Understanding: Strive to understand the underlying concepts of fractions, rather than simply memorizing rules and procedures. This will enable you to solve a wider range of fraction problems and apply your knowledge to new situations.
- Be Patient and Persistent: Learning fractions takes time and effort. Don't get discouraged if you don't understand everything right away. Be patient with yourself and keep practicing, and you'll eventually master fractions.
FAQ (Frequently Asked Questions)
- Q: What is a mixed number?
- A: A mixed number is a number consisting of a whole number and a proper fraction (e.g., 2 1/4).
- Q: How do I convert a mixed number to an improper fraction?
- A: Multiply the whole number by the denominator of the fraction, add the result to the numerator, and keep the same denominator.
- Q: What is an improper fraction?
- A: An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4).
- Q: How do I find half of a fraction?
- A: Multiply the fraction by 1/2.
- Q: Why is it important to understand fractions?
- A: Fractions are used in many real-world situations, including cooking, measurement, finance, and construction.
Conclusion
Finding half of 1 1/2 might seem daunting at first, but by understanding the fundamental principles of fractions and employing the right techniques, you can easily solve this problem. Remember to convert mixed numbers to improper fractions, and then multiply by 1/2. You can also visualize the problem or use the distributive property to arrive at the correct answer, which is 3/4. Mastering fractions is a valuable skill that will benefit you in many areas of life. Practice regularly, and don't be afraid to seek help when needed.
How do you plan to apply these fraction skills in your daily life? Are you ready to tackle more complex fraction problems now?
Latest Posts
Latest Posts
-
Definition Of Inclusion In Special Education
Dec 06, 2025
-
What Do Fungi And Bacteria Have In Common
Dec 06, 2025
-
What Are The Musical Instrument Families
Dec 06, 2025
-
How Are Kinetic Energy And Potential Energy Related
Dec 06, 2025
-
Cual Es El Pais Mas Pequeno De Centro America
Dec 06, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 1 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.