Explain How To Create An Equation With Infinitely Many Solutions
pythondeals
Nov 01, 2025 · 9 min read
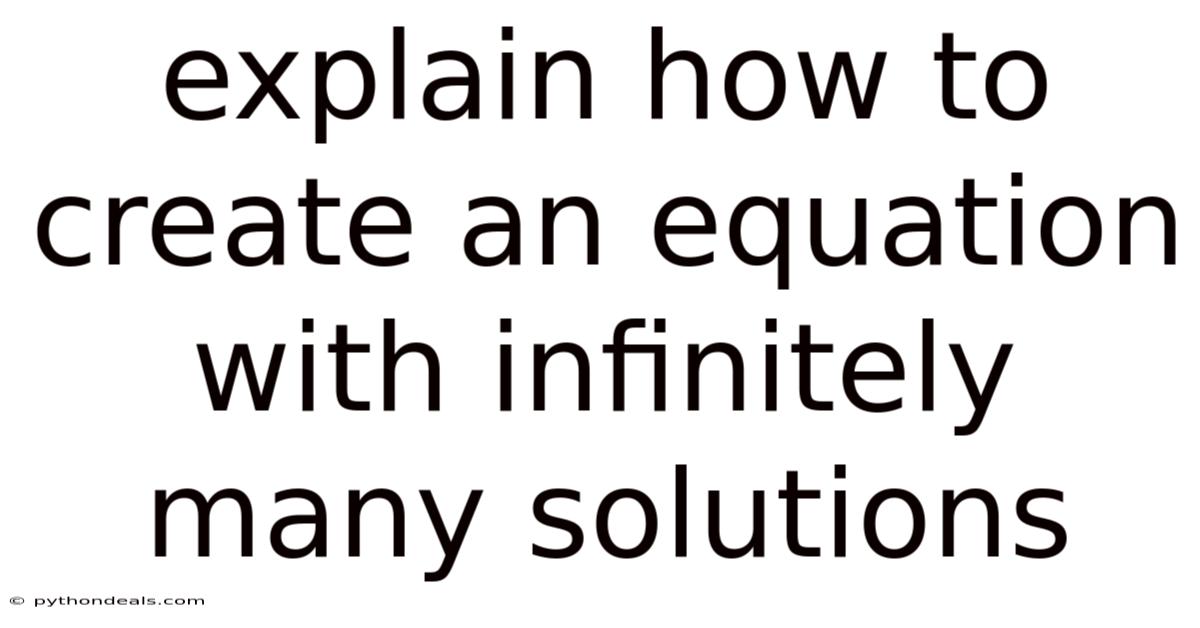
Table of Contents
The pursuit of mathematical solutions often leads us to a single, definitive answer. However, in the realm of equations, there exists a fascinating concept: equations with infinitely many solutions. These aren't your typical x = 5 scenarios. Instead, they represent a situation where any value substituted for the variable will satisfy the equation. This article delves into the mechanics of constructing such equations, providing a comprehensive guide for anyone seeking to master this intriguing aspect of algebra.
Introduction: The Allure of Infinite Solutions
Imagine an equation where you can plug in any number you desire, and the equation remains true. This is the essence of an equation with infinitely many solutions. These equations are not simply mathematical anomalies; they highlight the fundamental properties of equality and offer valuable insights into algebraic manipulation. Unlike equations with a single solution or no solution, equations with infinite solutions reveal a deeper connection between the two sides of the equation, essentially making them different representations of the same mathematical statement.
The concept of infinitely many solutions is encountered in various branches of mathematics, including linear algebra, calculus, and differential equations. Understanding how to create and identify these equations is crucial for advanced problem-solving and theoretical understanding. This article will guide you through the process of creating such equations, providing clear examples and step-by-step instructions.
Understanding the Foundation: Equivalent Equations
The cornerstone of creating an equation with infinitely many solutions lies in the concept of equivalent equations. Equivalent equations are equations that, despite appearing different, have the same solution set. For an equation to have infinitely many solutions, both sides of the equation must be equivalent expressions. This means that after simplification, both sides will be identical.
To illustrate, consider the equation:
2x + 4 = 2(x + 2)
Expanding the right side of the equation gives:
2x + 4 = 2x + 4
As you can see, both sides are identical. This means that any value you substitute for 'x' will satisfy the equation. For example:
- If x = 0: 2(0) + 4 = 2(0 + 2) -> 4 = 4 (True)
- If x = 1: 2(1) + 4 = 2(1 + 2) -> 6 = 6 (True)
- If x = -1: 2(-1) + 4 = 2(-1 + 2) -> 2 = 2 (True)
This simple example highlights the core principle: an equation with infinitely many solutions is essentially a statement that is always true, regardless of the variable's value.
Step-by-Step Guide: Creating Equations with Infinite Solutions
Now, let's break down the process of creating these equations into manageable steps:
-
Step 1: Start with a Basic Expression: Begin by creating a simple algebraic expression. This will form one side of your equation. For instance, let's start with the expression:
3x + 6
-
Step 2: Manipulate the Expression: Use algebraic manipulations to create an equivalent expression. Common techniques include:
- Distributive Property: Multiply a term by an expression inside parentheses.
- Factoring: Extract a common factor from multiple terms.
- Combining Like Terms: Simplify the expression by adding or subtracting similar terms.
In our example, we can factor out a 3 from the expression:
3(x + 2)
-
Step 3: Form the Equation: Set the original expression equal to its manipulated form. This creates the equation with infinitely many solutions:
3x + 6 = 3(x + 2)
-
Step 4: Verify the Equivalence: To ensure that the equation has infinitely many solutions, simplify both sides of the equation. If the simplified forms are identical, the equation is valid.
Expanding the right side of our equation gives:
3x + 6 = 3x + 6
Since both sides are the same, the equation 3x + 6 = 3(x + 2) indeed has infinitely many solutions.
Examples with Varying Complexity
To further illustrate the process, let's explore several examples with increasing complexity:
-
Example 1: Simple Linear Equation
- Start with: 4x - 8
- Manipulate: 4(x - 2)
- Equation: 4x - 8 = 4(x - 2)
Verification: Expanding the right side gives 4x - 8 = 4x - 8.
-
Example 2: Equation with Multiple Terms
- Start with: 2x + 3y - 5
- Manipulate: 2x + 3y - 5 + (0) (Adding zero in a creative way)
- Rewrite Zero: 2x + 3y - 5 + (x - x) + (y - y) + (1 - 1)
- Rearrange: (2x + x - x) + (3y + y - y) + (-5 + 1 - 1)
- Simplify: 3x-x + 4y-y - 5 -1 +1
- Equation: 2x + 3y - 5 = 3x-x + 4y-y - 5 -1 +1
Verification: Simplifying both sides will lead back to 2x + 3y - 5 = 2x + 3y - 5. In this case, while x and y can vary infinitely, they are connected (or dependent).
-
Example 3: Quadratic Equation
- Start with: x^2 + 4x + 4
- Manipulate: (x + 2)(x + 2) or (x+2)^2
- Equation: x^2 + 4x + 4 = (x + 2)^2
Verification: Expanding the right side gives x^2 + 4x + 4 = x^2 + 4x + 4.
-
Example 4: More Complex Linear Equation
- Start with: 5x - 2(x + 3)
- Manipulate: 5x - 2x - 6 = 3x - 6
- Further manipulate: 3(x - 2)
- Equation: 5x - 2(x + 3) = 3(x - 2)
Verification: Expanding both sides gives 5x - 2x - 6 = 3x - 6, which simplifies to 3x - 6 = 3x - 6.
-
Example 5: Rational Equation (Be Cautious with Restrictions)
- Start with: (x^2 - 1) / (x + 1) (Note: x cannot be -1)
- Manipulate: [(x + 1)(x - 1)] / (x + 1) = x - 1
- Equation: (x^2 - 1) / (x + 1) = x - 1
Verification: Simplifying the left side yields x - 1 = x - 1, provided x ≠ -1. Technically, because of the restriction, this isn't perfectly infinite solutions. It's infinite except for one single point. However, it's a good example of where this concept can be applied with a nuanced understanding.
Advanced Techniques and Considerations
While the basic principle of creating equivalent expressions is straightforward, mastering the art of generating equations with infinitely many solutions involves understanding more advanced techniques and considerations:
-
Using Identities: Leverage trigonometric, logarithmic, and algebraic identities to create equivalent expressions. For example:
- sin^2(x) + cos^2(x) = 1
- log(ab) = log(a) + log(b)
-
Parameterization: Introduce a parameter to create a family of equivalent expressions. This is particularly useful in linear algebra and differential equations.
-
Restrictions and Domains: Be mindful of restrictions on the variables. Certain operations, such as division by zero or taking the logarithm of a negative number, can introduce limitations on the solution set. As seen in Example 5, these restrictions must be clearly stated to avoid misinterpretations.
-
Matrices: In linear algebra, you can create systems of equations with infinitely many solutions. This happens when the number of variables exceeds the number of independent equations, leading to a situation where there are free variables that can take on any value, resulting in infinite solutions.
Identifying Equations with Infinite Solutions
Knowing how to create these equations is only half the battle. Recognizing them when you encounter them in a problem is equally important. Here are key indicators:
- Simplification Leads to Identity: The most direct way is to simplify both sides of the equation. If they become identical, you have an equation with infinitely many solutions.
- Zero Equals Zero: When solving the equation, if you arrive at a statement like 0 = 0, this indicates that the equation is true for all values of the variable.
- Dependent Equations: In a system of equations, if one equation is a multiple of another, they are dependent and contribute to infinite solutions (or no solutions if they are contradictory).
- Graphical Representation: For single-variable equations, if the graph of both sides of the equation is the same line, it signifies infinitely many solutions. For systems of two-variable equations, infinite solutions occur when the lines representing the equations are coincident (overlap).
Common Pitfalls to Avoid
- Incorrect Simplification: Double-check your algebraic manipulations to avoid errors that could lead to incorrect conclusions.
- Ignoring Restrictions: Always consider restrictions on variables, especially in rational and logarithmic equations.
- Assuming All Equations with Variables on Both Sides Have One Solution: This is a common misconception. Always simplify before drawing conclusions.
The Significance of Infinite Solutions in Advanced Mathematics
The concept of infinite solutions extends far beyond basic algebra and plays a vital role in more advanced mathematical fields:
- Linear Algebra: In systems of linear equations, infinite solutions arise when the system is underdetermined (more variables than equations) or when equations are linearly dependent. This is crucial in fields like computer graphics, data analysis, and optimization.
- Differential Equations: Many differential equations have infinitely many solutions, often represented by a family of functions. Understanding these families is essential for modeling physical phenomena like oscillations and population growth.
- Calculus: The concept of limits and continuity is closely related to infinite solutions. For example, a function may have a limit at a point even if it's not defined there, leading to infinitely many ways to "fill in" the missing value.
- Numerical Analysis: When solving equations numerically, algorithms may converge to a solution or indicate that there are infinitely many solutions or no solutions within a certain tolerance.
FAQ: Frequently Asked Questions
-
Q: Can an equation have infinitely many solutions for only a specific range of values?
- A: No. If an equation has infinitely many solutions, it must be true for all values of the variable within its domain (excluding any restricted values).
-
Q: How do I know if my equation truly has infinitely many solutions and isn't just very close?
- A: Simplify both sides algebraically. If they are identically the same, it's infinitely many solutions. Numerical approximation can be misleading.
-
Q: Is it possible to create an equation with infinitely many solutions but that is still false sometimes?
- A: No. The very definition of infinitely many solutions means the equation is always true (within its domain). If it's sometimes false, it's not infinitely many solutions.
-
Q: Can I have an equation with infinitely many solutions where the variable doesn't cancel out?
- A: Yes. For example,
2x + 4 = 2(x+2)simplifies to2x+4 = 2x+4. Thexterms don't disappear, but the equation is true regardless of the value ofx.
- A: Yes. For example,
-
Q: What's the difference between infinitely many solutions and no solution?
- A: Infinitely many solutions means the equation is always true (e.g., 0 = 0). No solution means the equation is never true (e.g., 0 = 1).
Conclusion: Embracing the Infinite
Creating and identifying equations with infinitely many solutions is a powerful skill that enhances your algebraic proficiency and deepens your understanding of mathematical principles. By mastering the art of equivalent expressions and being mindful of restrictions, you can confidently navigate the world of equations with infinite possibilities. Remember to always verify your results by simplifying both sides and ensuring that the equation holds true for all valid values of the variable.
The beauty of mathematics lies in its ability to reveal hidden connections and unexpected relationships. Equations with infinitely many solutions are a testament to this, showcasing the elegant interplay between variables and the boundless nature of mathematical truths. How will you apply this newfound knowledge to your future mathematical endeavors? What other mathematical concepts will you explore to further expand your understanding of the world around you?
Latest Posts
Related Post
Thank you for visiting our website which covers about Explain How To Create An Equation With Infinitely Many Solutions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.