Derivative Of X 2 X 2 3
pythondeals
Nov 21, 2025 · 9 min read
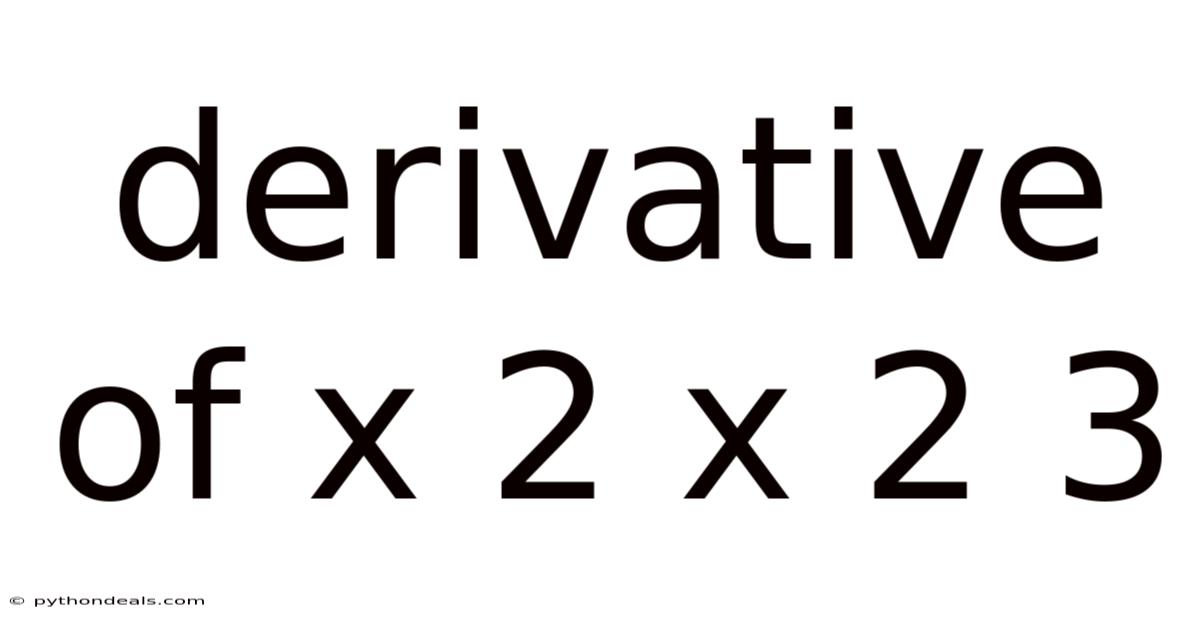
Table of Contents
Here's a comprehensive article on the derivative of x² + 2x + 3, designed to be educational, engaging, and optimized for readability and SEO:
Unlocking the Secrets: Mastering the Derivative of x² + 2x + 3
Have you ever wondered how mathematicians and scientists calculate the instantaneous rate of change of a curve? The concept of a derivative lies at the heart of this fascinating field. Let's embark on a journey to demystify the derivative of the quadratic expression x² + 2x + 3. Understanding this seemingly simple derivative unlocks a gateway to more complex calculus concepts and real-world applications.
Derivatives aren't just abstract mathematical concepts; they're the cornerstone of understanding motion, optimization, and various other phenomena in physics, engineering, and economics. In this article, we’ll break down the process step-by-step, making it accessible even if you're new to calculus.
What is a Derivative? The Essence of Change
At its core, a derivative represents the instantaneous rate of change of a function. Imagine you're driving a car. Your speedometer indicates your speed at any given moment. That's essentially a derivative – it tells you how your position (distance traveled) is changing with respect to time.
Mathematically, the derivative of a function f(x) is denoted as f'(x) (read as "f prime of x") or dy/dx (if y = f(x)). It's defined using the concept of a limit:
f'(x) = lim (h->0) [f(x + h) - f(x)] / h
This formula might look intimidating, but it simply formalizes the idea of finding the slope of a tangent line to the curve of the function at a specific point. The tangent line is the line that "just touches" the curve at that point, and its slope represents the instantaneous rate of change.
The Power Rule: Your Best Friend for Polynomials
Fortunately, we don't always have to resort to the limit definition to find derivatives. For polynomial functions (expressions with terms like x², x³, x, and constants), we have a powerful tool called the power rule.
The power rule states: If f(x) = xⁿ, then f'(x) = nxⁿ⁻¹.
In simpler terms, you multiply the term by the exponent and then reduce the exponent by 1. This rule is incredibly efficient for differentiating polynomial terms.
Deconstructing x² + 2x + 3: A Step-by-Step Guide
Now, let's apply the power rule and other essential derivative rules to find the derivative of our target expression, f(x) = x² + 2x + 3.
-
The Sum/Difference Rule: The derivative of a sum (or difference) of terms is the sum (or difference) of the derivatives of those individual terms. In other words, we can differentiate each term separately and then combine the results.
- f'(x) = d/dx (x²) + d/dx (2x) + d/dx (3)
-
Differentiating x²: Apply the power rule. Here, n = 2.
- d/dx (x²) = 2x²⁻¹ = 2x¹ = 2x
-
Differentiating 2x: We can use the constant multiple rule, which states that the derivative of a constant multiplied by a function is the constant multiplied by the derivative of the function.
- d/dx (2x) = 2 * d/dx (x)
- Since x is the same as x¹, applying the power rule gives us: d/dx (x) = 1x¹⁻¹ = 1x⁰ = 1
- Therefore, d/dx (2x) = 2 * 1 = 2
-
Differentiating 3: The derivative of any constant is always zero. This is because a constant doesn't change, so its rate of change is zero.
- d/dx (3) = 0
-
Putting it All Together: Now, combine the derivatives of each term:
- f'(x) = 2x + 2 + 0
- f'(x) = 2x + 2
Therefore, the derivative of x² + 2x + 3 is 2x + 2.
Visualizing the Derivative: Connecting Algebra to Geometry
The derivative 2x + 2 represents the slope of the tangent line to the curve y = x² + 2x + 3 at any point x. Let's visualize this:
- The graph of y = x² + 2x + 3 is a parabola.
- The derivative y' = 2x + 2 is a linear function.
For example:
- At x = -2, the slope of the tangent line to the parabola is 2(-2) + 2 = -2. The tangent line is decreasing (negative slope).
- At x = -1, the slope of the tangent line is 2(-1) + 2 = 0. The tangent line is horizontal (zero slope). This is the vertex of the parabola, where it changes direction.
- At x = 0, the slope of the tangent line is 2(0) + 2 = 2. The tangent line is increasing (positive slope).
This visual connection between the derivative and the tangent line reinforces the fundamental concept of the derivative as an instantaneous rate of change.
Why is the Derivative of a Constant Zero? A Deeper Look
The fact that the derivative of a constant is zero often raises questions. Let's understand why this is the case.
Consider the constant function f(x) = c, where c is any constant (e.g., 3, -5, π). No matter what value of x you input into the function, the output is always c. The graph of this function is a horizontal line.
The slope of a horizontal line is always zero. Since the derivative represents the slope of the tangent line, and the tangent line to a horizontal line is the line itself, the derivative of a constant function must be zero.
Mathematically, using the limit definition:
f'(x) = lim (h->0) [f(x + h) - f(x)] / h
Since f(x) = c for all x, we have f(x + h) = c as well. Therefore:
f'(x) = lim (h->0) [c - c] / h = lim (h->0) 0 / h = lim (h->0) 0 = 0
This confirms that the derivative of a constant is always zero.
Applications of Derivatives: Beyond the Textbook
Derivatives are not just theoretical tools; they have wide-ranging applications in various fields:
- Physics: Derivatives are used to calculate velocity (the derivative of position with respect to time) and acceleration (the derivative of velocity with respect to time). Understanding motion relies heavily on derivatives.
- Engineering: Engineers use derivatives to optimize designs, such as minimizing the drag on an aircraft wing or maximizing the strength of a bridge.
- Economics: Economists use derivatives to analyze marginal cost and marginal revenue, helping businesses make optimal decisions about production and pricing.
- Computer Science: Derivatives are used in machine learning algorithms, particularly in gradient descent, to find the minimum of a cost function. This allows algorithms to learn from data.
- Optimization Problems: Derivatives are crucial for finding maximum and minimum values of functions. This is essential in many applications, such as maximizing profit, minimizing cost, or finding the shortest distance.
Tips for Mastering Derivatives
- Practice Regularly: The key to mastering derivatives is consistent practice. Work through a variety of examples, starting with simple polynomials and progressing to more complex functions.
- Understand the Rules: Memorize and understand the basic derivative rules (power rule, constant multiple rule, sum/difference rule, product rule, quotient rule, chain rule).
- Visualize the Concepts: Use graphs and diagrams to visualize the relationship between a function and its derivative. This will help you develop a deeper understanding of the concepts.
- Use Online Resources: Take advantage of online resources such as Khan Academy, Wolfram Alpha, and Symbolab to practice problems and get help with challenging concepts.
- Don't Be Afraid to Ask Questions: If you're struggling with a particular concept, don't hesitate to ask your teacher, professor, or a tutor for help.
Advanced Techniques: Beyond the Basics
While we focused on the power rule, constant multiple rule, and sum/difference rule, there are more advanced techniques for finding derivatives of more complex functions. These include:
- The Product Rule: Used to differentiate the product of two functions: d/dx [u(x)v(x)] = u'(x)v(x) + u(x)v'(x)
- The Quotient Rule: Used to differentiate the quotient of two functions: d/dx [u(x)/v(x)] = [u'(x)v(x) - u(x)v'(x)] / [v(x)]²
- The Chain Rule: Used to differentiate composite functions (functions within functions): d/dx [f(g(x))] = f'(g(x)) * g'(x)
Mastering these rules expands your ability to differentiate a wider range of functions.
FAQ (Frequently Asked Questions)
- Q: What is the difference between a derivative and an integral?
- A: A derivative is the instantaneous rate of change of a function, while an integral is the area under the curve of a function. They are inverse operations of each other (fundamental theorem of calculus).
- Q: Why is calculus important?
- A: Calculus provides the tools to model and analyze change and motion, making it essential in science, engineering, economics, and many other fields.
- Q: Can I use a calculator to find derivatives?
- A: Yes, many calculators have built-in functions for finding derivatives. However, it's important to understand the underlying concepts and rules so you can solve problems effectively.
- Q: What is a higher-order derivative?
- A: A higher-order derivative is the derivative of a derivative. For example, the second derivative is the derivative of the first derivative, the third derivative is the derivative of the second derivative, and so on. They provide information about the concavity and inflection points of a function.
- Q: How does the derivative relate to optimization problems?
- A: Derivatives are used to find critical points (where the derivative is zero or undefined) of a function. These critical points can be local maxima, local minima, or saddle points. By analyzing the first and second derivatives, you can determine the nature of these critical points and solve optimization problems (finding maximum or minimum values).
Conclusion
Understanding the derivative of x² + 2x + 3 is more than just a mathematical exercise; it's a gateway to grasping fundamental concepts in calculus and their vast applications. By mastering the power rule, constant multiple rule, and sum/difference rule, you can confidently differentiate polynomial expressions and unlock the power of calculus. Remember to practice regularly, visualize the concepts, and don't hesitate to seek help when needed.
Calculus is a fascinating and powerful tool that can help you understand the world around you in new and exciting ways. So, embrace the challenge, explore the concepts, and unlock your mathematical potential!
How do you plan to apply your newfound understanding of derivatives to solve real-world problems? Are you excited to explore more advanced calculus concepts?
Latest Posts
Latest Posts
-
According To The Law Of Conservation Of Mass
Nov 21, 2025
-
What Are Affirmative Commands In Spanish
Nov 21, 2025
-
Dow Jones Total Completion Stock Market Index
Nov 21, 2025
-
Create A New Table Using Table Datasheet View
Nov 21, 2025
-
Acid Base Titration Weak Acid Strong Base
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.