Cos 2 X Sin 2 X
pythondeals
Nov 27, 2025 · 14 min read
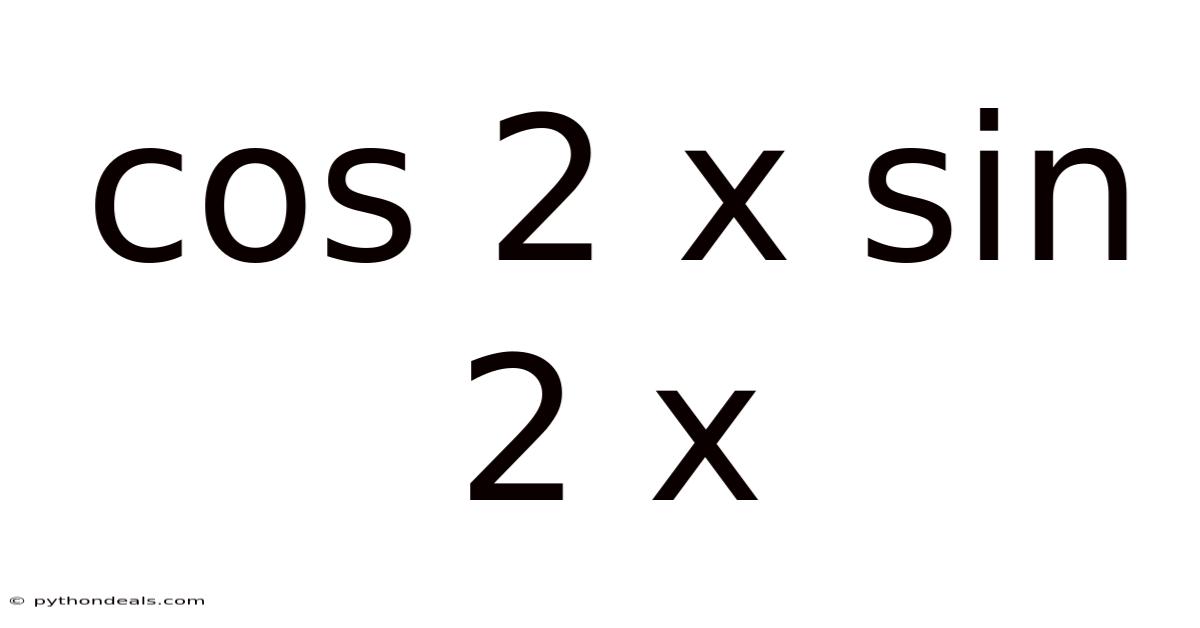
Table of Contents
In the realm of trigonometry, navigating through trigonometric identities and expressions can sometimes feel like deciphering a complex code. Among these trigonometric functions, cos 2x sin 2x presents an intriguing case. This expression, a product of cosine and sine functions with a doubled angle, is not just a mathematical curiosity but a fundamental building block in more advanced calculations and applications.
Understanding cos 2x sin 2x requires more than just memorizing formulas. It demands a deeper appreciation of how trigonometric identities interconnect and how we can manipulate them to simplify expressions, solve equations, and model real-world phenomena. In this comprehensive exploration, we will delve into the intricacies of cos 2x sin 2x, starting from the basics and gradually unraveling its applications and transformations. Whether you are a student seeking clarity or a seasoned professional brushing up on fundamentals, this guide aims to provide a thorough understanding of this trigonometric gem.
Introduction to cos 2x sin 2x
At its core, cos 2x sin 2x is a trigonometric expression that combines the cosine and sine functions, each with a doubled angle. To truly grasp its significance, we must first revisit the fundamental identities and properties that govern these functions. Understanding these basics will enable us to appreciate the elegance and utility of this expression.
The expression cos 2x sin 2x involves two primary trigonometric functions:
- Cosine (cos): In a right-angled triangle, the cosine of an angle is defined as the ratio of the adjacent side to the hypotenuse. The cosine function is periodic, oscillating between -1 and 1.
- Sine (sin): The sine of an angle in a right-angled triangle is the ratio of the opposite side to the hypotenuse. Like cosine, the sine function is also periodic and oscillates between -1 and 1.
Now, let’s explore the double angle formulas:
- Double Angle Formula for Cosine: The double angle formula for cosine can be expressed in three common forms:
- cos 2x = cos²x - sin²x
- cos 2x = 2cos²x - 1
- cos 2x = 1 - 2sin²x
- Double Angle Formula for Sine: The double angle formula for sine is given by:
- sin 2x = 2sin x cos x
These formulas are derived from the fundamental trigonometric identities and the angle sum formulas. They are essential for simplifying expressions and solving trigonometric equations. With this groundwork laid, we can now turn our attention to understanding and manipulating cos 2x sin 2x. This expression is not just a combination of these functions; it’s a gateway to understanding more complex trigonometric relationships and applications.
Comprehensive Overview of cos 2x sin 2x
To fully understand cos 2x sin 2x, we need to explore its properties, transformations, and potential applications. By examining its composition and how it interacts with other trigonometric identities, we can unlock deeper insights into its utility and significance.
Let's break down the expression cos 2x sin 2x step by step:
- Expanding the Expression: Using the double angle formulas, we can rewrite cos 2x sin 2x as follows:
- Substitute sin 2x = 2 sin x cos x:
- cos 2x sin 2x = cos 2x (2 sin x cos x)
- Further, substitute cos 2x with cos²x - sin²x:
- cos 2x sin 2x = (cos²x - sin²x) (2 sin x cos x)
- Distribute the terms:
- cos 2x sin 2x = 2 sin x cos³x - 2 sin³x cos x
- Substitute sin 2x = 2 sin x cos x:
- Factoring the Expression: The expanded form can be factored to reveal underlying symmetries:
- 2 sin x cos³x - 2 sin³x cos x = 2 sin x cos x (cos²x - sin²x)
- Recognize that 2 sin x cos x = sin 2x and cos²x - sin²x = cos 2x:
- cos 2x sin 2x = sin 2x cos 2x
- Further Simplification: Notice that the expression sin 2x cos 2x looks like half of the double angle formula for sine. To make this explicit, we can multiply and divide by 2:
- cos 2x sin 2x = (1/2) * 2 sin 2x cos 2x
- Using the double angle formula, 2 sin 2x cos 2x = sin 4x:
- cos 2x sin 2x = (1/2) sin 4x
Therefore, cos 2x sin 2x simplifies to (1/2) sin 4x. This transformation is highly useful because it converts a product of trigonometric functions into a single sine function with a different angle, which is often easier to handle in calculations and applications.
Understanding these transformations allows us to see cos 2x sin 2x not just as an isolated expression but as part of a broader network of trigonometric relationships. Recognizing this allows for efficient problem-solving and deeper insight into mathematical structures.
Trigonometric Identities and Transformations
The manipulation of trigonometric expressions heavily relies on identities that relate different trigonometric functions. These identities act as the fundamental rules of engagement, allowing us to transform complex expressions into simpler, more manageable forms.
- Pythagorean Identity: The most fundamental identity is the Pythagorean identity:
- sin²x + cos²x = 1
- This identity can be rearranged to express sin²x or cos²x in terms of the other, which is often useful in simplifying expressions.
- Double Angle Formulas: As previously mentioned, the double angle formulas are essential for dealing with expressions involving multiples of angles:
- sin 2x = 2 sin x cos x
- cos 2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x
- Sum and Difference Formulas: These formulas are used to express trigonometric functions of sums or differences of angles:
- sin(A + B) = sin A cos B + cos A sin B
- sin(A - B) = sin A cos B - cos A sin B
- cos(A + B) = cos A cos B - sin A sin B
- cos(A - B) = cos A cos B + sin A sin B
- Product-to-Sum Formulas: These formulas transform products of trigonometric functions into sums or differences:
- sin A cos B = (1/2) [sin(A + B) + sin(A - B)]
- cos A sin B = (1/2) [sin(A + B) - sin(A - B)]
- cos A cos B = (1/2) [cos(A + B) + cos(A - B)]
- sin A sin B = (1/2) [cos(A - B) - cos(A + B)]
- Half Angle Formulas: These formulas express trigonometric functions of half angles in terms of the original angle:
- sin(x/2) = ±√((1 - cos x) / 2)
- cos(x/2) = ±√((1 + cos x) / 2)
Understanding how to apply these identities is crucial for simplifying and manipulating trigonometric expressions. For example, let's revisit cos 2x sin 2x:
- Starting with cos 2x sin 2x, we can apply the double angle formula for sine:
- cos 2x sin 2x = cos 2x (2 sin x cos x)
- Then, we can use the double angle formula for cosine:
- cos 2x sin 2x = (cos²x - sin²x) (2 sin x cos x)
- By recognizing that 2 sin x cos x = sin 2x, we get:
- cos 2x sin 2x = cos 2x sin 2x
- Finally, multiplying and dividing by 2 and using the double angle formula for sine again:
- cos 2x sin 2x = (1/2) (2 sin 2x cos 2x) = (1/2) sin 4x
Applications of cos 2x sin 2x
While the expression cos 2x sin 2x may seem purely theoretical, it has significant applications in various fields. Understanding these applications helps to appreciate the real-world relevance of trigonometric identities and transformations.
- Physics:
- Wave Mechanics: In physics, particularly in wave mechanics, trigonometric functions are used to describe the behavior of waves. The expression cos 2x sin 2x can appear when analyzing wave interference patterns or in solving differential equations related to wave propagation.
- Harmonic Motion: Trigonometric functions are fundamental to describing simple harmonic motion. Expressions like cos 2x sin 2x can emerge when analyzing the superposition of different harmonic motions or when dealing with damped oscillations.
- Engineering:
- Signal Processing: In electrical engineering, signal processing often involves decomposing complex signals into simpler sinusoidal components using Fourier analysis. The expression cos 2x sin 2x can arise when analyzing modulated signals or in filter design.
- Structural Analysis: Trigonometric functions are used to analyze stresses and strains in structures. Expressions involving cos 2x sin 2x can appear when dealing with bending moments or shear forces in structural elements.
- Mathematics:
- Calculus: In calculus, trigonometric functions are frequently encountered in integration and differentiation problems. The expression cos 2x sin 2x can be integrated or differentiated using standard calculus techniques.
- Complex Analysis: In complex analysis, trigonometric functions are related to complex exponentials through Euler's formula. The expression cos 2x sin 2x can be expressed in terms of complex exponentials, which can simplify certain calculations.
- Computer Graphics:
- 3D Transformations: Trigonometric functions are used extensively in computer graphics for rotations, scaling, and translations of objects in 3D space. The expression cos 2x sin 2x can arise when calculating transformations involving multiple rotations or shears.
- Shading and Lighting: Trigonometric functions are also used in shading and lighting models to calculate the intensity of light reflected from surfaces. Expressions involving cos 2x sin 2x can appear when modeling specular reflections or diffuse lighting.
To illustrate, consider a simple example in wave mechanics: Suppose you have two waves described by the functions cos 2x and sin 2x. The product of these waves, cos 2x sin 2x, can be simplified to (1/2) sin 4x. This simplification allows for easier analysis of the resulting wave pattern, revealing its amplitude and frequency.
Advanced Techniques and Identities
As we delve deeper into trigonometry, it becomes evident that mastering advanced techniques and identities is essential for tackling complex problems. These techniques not only simplify calculations but also provide deeper insights into the relationships between trigonometric functions.
- Triple Angle Formulas: These formulas express trigonometric functions of triple angles in terms of the original angle:
- sin 3x = 3 sin x - 4 sin³x
- cos 3x = 4 cos³x - 3 cos x
- Power Reduction Formulas: These formulas reduce higher powers of trigonometric functions to lower powers, which is useful in integration and simplification:
- sin²x = (1 - cos 2x) / 2
- cos²x = (1 + cos 2x) / 2
- Weierstrass Substitution: Also known as the tangent half-angle substitution, this technique expresses trigonometric functions in terms of the tangent of half the angle:
- t = tan(x/2)
- sin x = (2t) / (1 + t²)
- cos x = (1 - t²) / (1 + t²)
- tan x = (2t) / (1 - t²)
- R-Formula: This formula expresses a sum of sine and cosine functions as a single trigonometric function with a phase shift:
- a cos x + b sin x = R cos(x - α)
- Where R = √(a² + b²) and α = arctan(b/a)
- Complex Numbers and Trigonometry: Complex numbers provide a powerful tool for analyzing trigonometric functions. Euler's formula relates complex exponentials to trigonometric functions:
- e^(ix) = cos x + i sin x
- This allows trigonometric functions to be expressed in terms of complex exponentials, which can simplify certain calculations and provide deeper insights into their properties.
For example, consider integrating cos²x sin²x. Using power reduction formulas, we can rewrite this as:
- cos²x sin²x = [(1 + cos 2x) / 2] [(1 - cos 2x) / 2]
- cos²x sin²x = (1 - cos²2x) / 4
- Using the power reduction formula again:
- cos²2x = (1 + cos 4x) / 2
- Substituting back:
- cos²x sin²x = (1 - (1 + cos 4x) / 2) / 4
- cos²x sin²x = (1 - cos 4x) / 8
- Now, the integral becomes:
- ∫ cos²x sin²x dx = ∫ (1 - cos 4x) / 8 dx
- ∫ cos²x sin²x dx = (1/8) ∫ (1 - cos 4x) dx
- ∫ cos²x sin²x dx = (1/8) [x - (1/4) sin 4x] + C
- ∫ cos²x sin²x dx = (x / 8) - (sin 4x / 32) + C
Tips & Expert Advice
As an educator and blogger, I’ve gathered a few tips and advice that can significantly enhance your understanding and application of trigonometric functions, particularly when dealing with expressions like cos 2x sin 2x.
- Master the Basic Identities: Before diving into complex problems, ensure you have a solid grasp of the fundamental trigonometric identities. These are the building blocks upon which all other techniques are based. Regularly practice manipulating these identities to become comfortable with their applications.
- Use Visual Aids: Trigonometry is inherently geometric, so using visual aids like unit circles and graphs can be incredibly helpful. Visualize the behavior of trigonometric functions and their relationships to gain a deeper understanding.
- Practice, Practice, Practice: The more you practice solving trigonometric problems, the more intuitive the techniques will become. Work through a variety of examples, starting with simple ones and gradually progressing to more complex problems.
- Learn to Recognize Patterns: Many trigonometric problems involve recognizing patterns and applying the appropriate identities. Develop the ability to spot these patterns quickly, which will save time and reduce errors.
- Use Technology Wisely: While it’s important to understand the underlying principles, don’t hesitate to use technology to check your work or explore complex expressions. Tools like graphing calculators and computer algebra systems can be valuable aids.
- Apply Transformations Strategically: When simplifying trigonometric expressions, think strategically about which transformations to apply. Sometimes, there are multiple approaches, but one may be more efficient than others.
- Check Your Work: Always double-check your work, especially when dealing with complex expressions. Trigonometric problems are prone to errors, so careful verification is essential.
- Relate to Real-World Applications: To make trigonometry more engaging and relevant, try to relate it to real-world applications. This will not only deepen your understanding but also make the subject more interesting.
Consider this practical tip: When faced with an expression like cos 2x sin 2x, always look for opportunities to apply the double angle formulas. This is often the key to simplifying the expression and revealing its underlying structure. Remember, cos 2x sin 2x can be transformed into (1/2) sin 4x, which is often easier to work with.
FAQ (Frequently Asked Questions)
To address common questions and misconceptions about cos 2x sin 2x and related trigonometric concepts, here is a concise FAQ:
- Q: What is the double angle formula for sin 2x?
- A: sin 2x = 2 sin x cos x
- Q: What is the double angle formula for cos 2x?
- A: cos 2x can be expressed in three forms: cos 2x = cos²x - sin²x, cos 2x = 2cos²x - 1, and cos 2x = 1 - 2sin²x
- Q: How can I simplify cos 2x sin 2x?
- A: cos 2x sin 2x can be simplified to (1/2) sin 4x using the double angle formulas.
- Q: Why are trigonometric identities important?
- A: Trigonometric identities allow us to simplify complex expressions, solve equations, and model real-world phenomena involving periodic functions.
- Q: What is the Pythagorean identity?
- A: The Pythagorean identity is sin²x + cos²x = 1.
- Q: Can you express cos 2x in terms of sine only?
- A: Yes, cos 2x = 1 - 2sin²x.
- Q: Can you express cos 2x in terms of cosine only?
- A: Yes, cos 2x = 2cos²x - 1.
- Q: How do you integrate cos²x sin²x?
- A: Integrate cos²x sin²x by using power reduction formulas to simplify the expression to (1 - cos 4x) / 8, then integrate term by term.
- Q: What are some real-world applications of trigonometric functions?
- A: Trigonometric functions are used in physics (wave mechanics, harmonic motion), engineering (signal processing, structural analysis), mathematics (calculus, complex analysis), and computer graphics (3D transformations, shading and lighting).
Conclusion
In summary, the expression cos 2x sin 2x is a valuable component of trigonometry, demonstrating the interconnectedness of trigonometric identities and their practical applications. By understanding its transformations and simplifications, you can tackle a wide range of problems in various fields. Mastering the double angle formulas and other trigonometric identities not only enhances your mathematical skills but also deepens your appreciation for the elegance and utility of trigonometry.
We’ve explored how cos 2x sin 2x can be simplified to (1/2) sin 4x, which often makes it easier to work with in calculations and applications. We’ve also discussed the importance of mastering basic trigonometric identities, using visual aids, practicing regularly, and relating trigonometry to real-world scenarios. These tips and techniques are essential for building a solid foundation in trigonometry and excelling in related fields.
As you continue your exploration of trigonometry, remember that practice and persistence are key. The more you work with these concepts, the more intuitive they will become. Embrace the challenge, and don’t hesitate to seek help when needed. Trigonometry is a rewarding subject that offers powerful tools for understanding and modeling the world around us.
How do you plan to apply these insights in your future studies or projects?
Latest Posts
Latest Posts
-
Which Of The Following Gives A Word Meaning
Nov 27, 2025
-
Epithelial Tissue In Proximal Convoluted Tubule
Nov 27, 2025
-
Add Mixed Fractions With Unlike Denominators
Nov 27, 2025
-
How To Make A Topographic Profile
Nov 27, 2025
-
Labelled Diagram Of Parts Of A Flower
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about Cos 2 X Sin 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.