A Negative Number Plus A Positive Number
pythondeals
Nov 07, 2025 · 8 min read
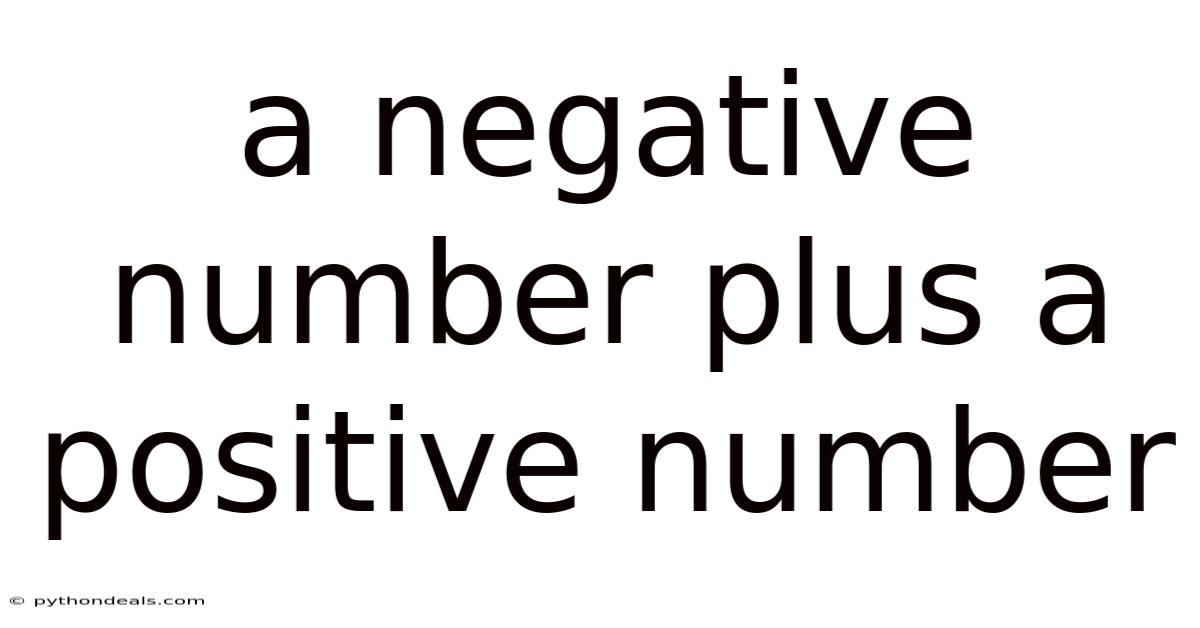
Table of Contents
Navigating the world of mathematics can sometimes feel like traversing a landscape filled with peaks and valleys. You might find yourself confidently ascending a well-known concept, only to stumble into an unexpected dip. One such area that often causes a bit of confusion is the interaction between negative and positive numbers. While the basic principles of addition and subtraction are usually straightforward, adding a negative number to a positive number (or vice versa) introduces a layer of complexity that necessitates a deeper understanding.
This article aims to provide a comprehensive guide to mastering the art of adding negative numbers to positive numbers. We'll break down the concept into digestible parts, explore real-world applications, and equip you with the tools and techniques needed to confidently tackle any problem involving this seemingly tricky operation. Whether you're a student struggling with algebra, a professional needing a refresher, or simply someone curious about the intricacies of mathematics, this guide will serve as your reliable companion.
Unveiling the Basics: Understanding Positive and Negative Numbers
Before diving into the specifics of adding negative and positive numbers, it's crucial to establish a solid understanding of what these numbers represent. Positive numbers are those greater than zero, representing quantities we can count, measure, or possess. They extend infinitely in one direction on the number line. Negative numbers, on the other hand, are those less than zero. They represent the opposite of positive quantities. Think of owing money (debt) or measuring temperatures below zero.
The number line is a powerful visual tool for understanding positive and negative numbers. Imagine a straight line with zero at the center. Positive numbers are located to the right of zero, increasing as you move further right. Negative numbers reside to the left of zero, decreasing (becoming more negative) as you move further left. This visual representation is particularly helpful when visualizing addition and subtraction.
The Mechanics of Addition: Combining Positive and Negative Quantities
At its core, addition is the process of combining two or more quantities to find their total. When dealing with positive numbers, this concept is intuitive. For example, 3 + 4 = 7 simply means combining three items with four items results in a total of seven items. However, when we introduce negative numbers, the process requires a slightly different perspective.
Adding a negative number to a positive number is essentially the same as subtracting the absolute value of the negative number from the positive number. The absolute value of a number is its distance from zero on the number line, regardless of direction. It's always a positive value or zero. For example, the absolute value of -5 is 5, written as |-5| = 5.
Therefore, the expression 5 + (-3) can be interpreted as "start at 5 and move 3 units to the left on the number line." This is equivalent to 5 - 3, which equals 2.
Rule of Thumb: Simplifying Addition with Negative Numbers
To simplify the process, remember this key rule: Adding a negative number is the same as subtracting a positive number.
Here are a few examples to illustrate this principle:
- 7 + (-2) = 7 - 2 = 5
- 10 + (-5) = 10 - 5 = 5
- -3 + 8 = 8 - 3 = 5 (Remember that the order of addition doesn't change the result)
Scenarios and Examples: Putting Theory into Practice
Let's explore some practical scenarios to solidify your understanding of adding negative and positive numbers:
Scenario 1: Bank Account Balance
Imagine you have $100 in your bank account. This is represented as +$100. You then spend $30, which can be represented as -$30 (a withdrawal). Your new balance is:
$100 + (-$30) = $100 - $30 = $70
You now have $70 in your account.
Scenario 2: Temperature Changes
The temperature is initially 5 degrees Celsius. It then drops by 8 degrees Celsius. This can be represented as:
5 + (-8) = 5 - 8 = -3
The new temperature is -3 degrees Celsius.
Scenario 3: Football Field
A football team starts at the 20-yard line. They gain 15 yards on one play (+15) and then lose 7 yards on the next play (-7). Their new position is:
20 + 15 + (-7) = 20 + 15 - 7 = 28
They are now at the 28-yard line.
Scenario 4: Altitude
You are standing on a hill that is 50 meters above sea level (+50). You then descend 75 meters (-75). Your new altitude relative to sea level is:
50 + (-75) = 50 - 75 = -25
You are now 25 meters below sea level.
The Number Line Visualization: A Powerful Tool
The number line is an invaluable tool for visualizing addition with negative numbers. To add a positive number, move to the right on the number line. To add a negative number, move to the left.
For example, to calculate -2 + 5:
- Start at -2 on the number line.
- Move 5 units to the right (because you are adding a positive number).
- You will end up at 3.
Therefore, -2 + 5 = 3.
Similarly, to calculate 4 + (-6):
- Start at 4 on the number line.
- Move 6 units to the left (because you are adding a negative number).
- You will end up at -2.
Therefore, 4 + (-6) = -2.
Addressing Common Misconceptions
One common misconception is that adding a negative number always results in a negative answer. This is not true. The result depends on the magnitude of the positive and negative numbers being added. If the absolute value of the positive number is greater than the absolute value of the negative number, the result will be positive. If the absolute value of the negative number is greater, the result will be negative. If the absolute values are equal, the result will be zero.
Another misconception is that adding a negative number is different from subtracting a positive number. As we have established, these are equivalent operations. Understanding this equivalence is key to mastering addition with negative numbers.
More Complex Scenarios and Examples
Let's delve into more complex examples to further refine your skills.
Example 1: Multiple Additions
Calculate: 12 + (-5) + (-3) + 7
- Combine the positive numbers: 12 + 7 = 19
- Combine the negative numbers: -5 + (-3) = -8
- Add the results: 19 + (-8) = 19 - 8 = 11
Therefore, 12 + (-5) + (-3) + 7 = 11.
Example 2: Dealing with Larger Numbers
Calculate: -45 + 72
- Recognize that this is the same as 72 - 45.
- Perform the subtraction: 72 - 45 = 27
Therefore, -45 + 72 = 27.
Example 3: Practical Application - Business Finances
A business has revenues of $5000 (+5000) and expenses of $6200 (-6200). What is the business's net profit or loss?
5000 + (-6200) = 5000 - 6200 = -1200
The business has a net loss of $1200.
The Importance of Understanding Signed Numbers in Advanced Mathematics
The concepts discussed here aren't just confined to basic arithmetic. A firm grasp of signed numbers is fundamental to success in more advanced mathematical fields, including:
- Algebra: Solving equations and inequalities often involves manipulating signed numbers.
- Calculus: Understanding limits, derivatives, and integrals relies heavily on working with positive and negative values.
- Physics: Many physical quantities, such as velocity, acceleration, and electric charge, are represented by signed numbers.
- Computer Science: Signed numbers are used to represent various data types and perform arithmetic operations in computer programs.
Mastering the Art: Tips and Techniques
Here are some practical tips to help you master the art of adding negative and positive numbers:
- Visualize the Number Line: Always use the number line to visualize the process, especially when you are starting out.
- Convert Addition to Subtraction: Remember that adding a negative number is the same as subtracting a positive number.
- Group Like Signs: When dealing with multiple additions, group positive and negative numbers separately before combining them.
- Practice Regularly: The more you practice, the more comfortable you will become with these operations.
- Use Real-World Examples: Relate the concepts to real-world scenarios to make them more meaningful.
- Don't Be Afraid to Ask for Help: If you are struggling, don't hesitate to seek assistance from teachers, tutors, or online resources.
Frequently Asked Questions (FAQ)
Q: Is adding a negative number always negative?
A: No. The result depends on the magnitudes of the positive and negative numbers. If the absolute value of the positive number is greater, the result will be positive.
Q: What is the absolute value?
A: The absolute value of a number is its distance from zero on the number line, regardless of direction. It's always a positive value or zero.
Q: How does the number line help with addition?
A: Moving to the right on the number line represents adding a positive number, while moving to the left represents adding a negative number.
Q: What is the difference between adding a negative number and subtracting a positive number?
A: There is no difference. They are equivalent operations.
Q: Why is it important to understand signed numbers?
A: A firm grasp of signed numbers is crucial for success in advanced mathematical fields such as algebra, calculus, physics, and computer science.
Conclusion
Adding negative numbers to positive numbers might seem daunting at first, but with a clear understanding of the underlying principles, visualization techniques, and consistent practice, it can become a straightforward and even enjoyable process. Remember the key concepts: the number line, the equivalence of adding a negative number and subtracting a positive number, and the importance of absolute value. By mastering these fundamentals, you will not only conquer this specific mathematical operation but also lay a solid foundation for future success in more advanced mathematical endeavors.
Now that you've explored the ins and outs of adding negative and positive numbers, how do you plan to apply this knowledge in your daily life or future studies? What strategies will you use to reinforce your understanding and avoid common pitfalls? The journey of mathematical learning is a continuous process, and your dedication to understanding these foundational concepts will undoubtedly pave the way for greater achievements.
Latest Posts
Latest Posts
-
Determine The Degree Of The Polynomial
Nov 07, 2025
-
How To Find Grams Per Mole
Nov 07, 2025
-
Bacteria And Are Collectively Referred To As Prokaryotes
Nov 07, 2025
-
How Do You Simplify Fractions With Square Roots
Nov 07, 2025
-
What Is The Difference Between Absolute Threshold And Difference Threshold
Nov 07, 2025
Related Post
Thank you for visiting our website which covers about A Negative Number Plus A Positive Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.