6 - 1 X 0 + 2 / 2
pythondeals
Nov 14, 2025 · 9 min read
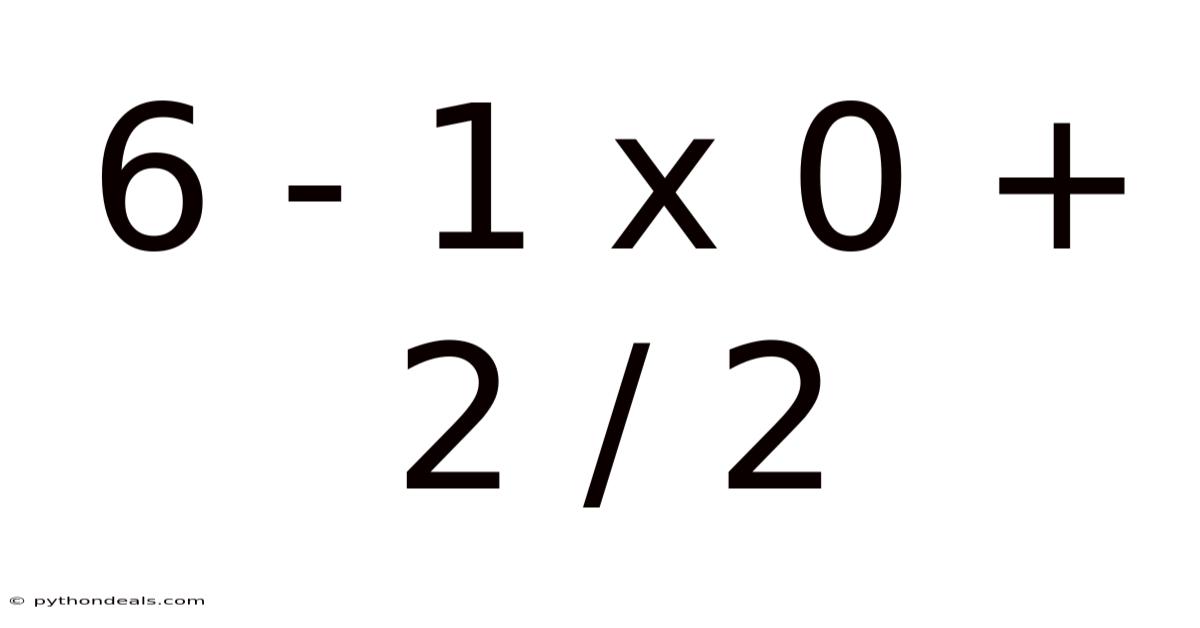
Table of Contents
Alright, let's break down the mathematical expression "6 - 1 x 0 + 2 / 2" and explore the fascinating world of order of operations, common mistakes, and the fundamental principles that govern how we solve mathematical problems. This might seem like a simple problem, but it highlights critical concepts that are essential for accurate calculations and understanding mathematical logic.
Introduction: The Power of Order
At first glance, the expression "6 - 1 x 0 + 2 / 2" might appear straightforward. However, without a clear understanding of the order of operations, you might arrive at an incorrect answer. This expression perfectly demonstrates why mathematical conventions are crucial for ensuring consistency and accuracy in calculations. These conventions, known as the order of operations, dictate the sequence in which we perform different mathematical operations. The most common mnemonic for remembering this order is PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). Adhering to this order is not just a matter of following rules; it's about maintaining the integrity and logical structure of mathematics.
The order of operations ensures that everyone, regardless of their location or background, arrives at the same correct answer when solving a mathematical problem. Imagine the chaos if different people followed different orders of operations! Consistency is paramount, and understanding PEMDAS is the key to unlocking accurate mathematical solutions. In this article, we will dissect the expression "6 - 1 x 0 + 2 / 2," explain the step-by-step process of solving it correctly, and delve into the underlying principles that make the order of operations so vital.
Decoding "6 - 1 x 0 + 2 / 2": A Step-by-Step Guide
To correctly solve the expression "6 - 1 x 0 + 2 / 2," we must adhere to the order of operations, commonly remembered as PEMDAS. Let's break down each step:
-
Multiplication and Division (from left to right):
- First, we address the multiplication: 1 x 0 = 0.
- Next, we handle the division: 2 / 2 = 1.
- The expression now simplifies to: 6 - 0 + 1.
-
Addition and Subtraction (from left to right):
- Starting from the left, we perform the subtraction: 6 - 0 = 6.
- Then, we perform the addition: 6 + 1 = 7.
Therefore, the correct answer to the expression "6 - 1 x 0 + 2 / 2" is 7. This step-by-step approach highlights the importance of following the correct order to avoid errors and arrive at the accurate result.
The Importance of PEMDAS: A Comprehensive Overview
PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) is the cornerstone of mathematical operations. It is a set of rules that dictate the sequence in which mathematical operations should be performed to ensure accuracy and consistency. Let's delve deeper into each component of PEMDAS:
-
Parentheses: Operations within parentheses (or brackets) are always performed first. This allows you to group parts of an expression and prioritize their calculation. For example, in the expression 2 x (3 + 4), you would first add 3 and 4 to get 7, and then multiply by 2 to get 14.
-
Exponents: Exponents indicate the power to which a number is raised. For example, in the expression 3^2 (3 squared), you would calculate 3 x 3, which equals 9. Exponents are performed after parentheses but before multiplication, division, addition, and subtraction.
-
Multiplication and Division: These operations are performed from left to right. It's important to note that multiplication and division have equal priority, so you perform whichever comes first as you read the expression from left to right. For example, in the expression 10 / 2 x 3, you would first divide 10 by 2 to get 5, and then multiply by 3 to get 15.
-
Addition and Subtraction: Similar to multiplication and division, addition and subtraction are performed from left to right. They also have equal priority. For example, in the expression 8 - 3 + 2, you would first subtract 3 from 8 to get 5, and then add 2 to get 7.
The order of operations is not arbitrary; it is a fundamental convention that ensures mathematical expressions are unambiguous and can be interpreted consistently. Without PEMDAS, the same expression could yield different results depending on the order in which operations are performed, leading to confusion and errors.
Common Pitfalls and How to Avoid Them
Even with a solid understanding of PEMDAS, it's easy to make mistakes if you're not careful. Here are some common pitfalls to watch out for:
-
Forgetting the Order: One of the most common mistakes is simply forgetting the correct order of operations. This can lead to performing addition or subtraction before multiplication or division, resulting in an incorrect answer.
- Solution: Always write out the PEMDAS mnemonic as a reminder and consciously follow the order.
-
Misinterpreting Left-to-Right Rule: It's crucial to remember that multiplication and division (and addition and subtraction) are performed from left to right. Many people mistakenly assume that multiplication always comes before division, or addition always comes before subtraction, regardless of their position in the expression.
- Solution: Carefully read the expression from left to right and perform the operations in the order they appear.
-
Ignoring Parentheses: Parentheses are powerful tools for overriding the default order of operations. Failing to recognize and address parentheses first can lead to significant errors.
- Solution: Always start by simplifying any expressions within parentheses before moving on to other operations.
-
Rushing Through the Problem: Rushing through a problem increases the likelihood of making careless errors. It's important to take your time, double-check your work, and ensure you're following each step correctly.
- Solution: Work methodically and deliberately, checking each step before proceeding to the next.
By being aware of these common pitfalls and actively working to avoid them, you can significantly improve your accuracy and confidence in solving mathematical expressions.
Real-World Applications of Order of Operations
The order of operations is not just an abstract mathematical concept; it has numerous practical applications in various fields. Here are a few examples:
-
Computer Programming: In programming, the order of operations is crucial for writing code that performs calculations correctly. Programming languages use a similar set of rules to PEMDAS to determine the order in which operations are executed. Incorrectly applying the order of operations in code can lead to bugs and unexpected results.
-
Financial Calculations: Financial calculations often involve complex formulas with multiple operations. Whether you're calculating interest rates, investment returns, or loan payments, it's essential to follow the order of operations to ensure accurate results. A small error in the order of operations can lead to significant discrepancies in financial calculations.
-
Engineering: Engineers use mathematical models and calculations to design and analyze structures, systems, and processes. The order of operations is critical for ensuring that these calculations are accurate and reliable. Incorrect calculations can have serious consequences in engineering applications, potentially leading to structural failures or other safety hazards.
-
Science: Scientific calculations often involve complex formulas with multiple variables and operations. Whether you're calculating the trajectory of a projectile, the rate of a chemical reaction, or the energy of a particle, it's essential to follow the order of operations to ensure accurate results.
These examples illustrate that the order of operations is a fundamental skill that is essential for success in many different fields. Understanding and applying PEMDAS correctly can help you avoid errors, improve your accuracy, and make informed decisions in various real-world situations.
Advanced Applications and Extensions
While the basic order of operations is straightforward, there are some advanced applications and extensions that are worth exploring:
-
Nested Parentheses: Expressions can contain nested parentheses, where one set of parentheses is inside another. In these cases, you work from the innermost parentheses outward. For example, in the expression 2 x (3 + (4 x 2)), you would first calculate 4 x 2, then add 3, and finally multiply by 2.
-
Complex Fractions: Complex fractions involve fractions within fractions. To simplify complex fractions, you need to apply the order of operations to both the numerator and the denominator before dividing.
-
Functions: Functions are mathematical operations that take one or more inputs and produce an output. Functions are typically performed before other operations, similar to parentheses. For example, in the expression sin(30) + 2, you would first calculate the sine of 30 degrees and then add 2.
-
Operator Precedence in Programming: Different programming languages may have slightly different rules for operator precedence. It's important to consult the documentation for the specific language you're using to ensure that you're following the correct order of operations.
These advanced applications and extensions demonstrate that the order of operations is a flexible and powerful tool that can be applied to a wide range of mathematical problems. By mastering the basic principles of PEMDAS and understanding how to apply them in more complex situations, you can significantly enhance your mathematical skills and problem-solving abilities.
FAQ (Frequently Asked Questions)
-
Q: What if I forget the order of operations?
- A: Use the mnemonic PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) to help you remember the correct order.
-
Q: Does multiplication always come before division?
- A: No, multiplication and division have equal priority and are performed from left to right.
-
Q: What if an expression has no parentheses?
- A: Follow the order of operations (PEMDAS) without the parentheses step.
-
Q: Why is the order of operations important?
- A: The order of operations ensures that mathematical expressions are unambiguous and can be interpreted consistently, leading to accurate and reliable results.
-
Q: Can I use a calculator to solve expressions with multiple operations?
- A: Yes, but be sure to enter the expression correctly and understand how your calculator handles the order of operations. Many calculators follow PEMDAS automatically.
Conclusion: Mastering the Fundamentals
The expression "6 - 1 x 0 + 2 / 2" might seem simple, but it underscores the critical importance of understanding and applying the order of operations. By following PEMDAS, we can ensure accuracy and consistency in our mathematical calculations. From computer programming to financial analysis, the order of operations is a fundamental skill that is essential for success in many different fields. So, embrace the power of PEMDAS and continue to refine your mathematical abilities.
How do you feel about the importance of order of operations in everyday calculations? Are you ready to tackle more complex mathematical challenges with confidence?
Latest Posts
Latest Posts
-
What Is Gram Positive Cocci In Clusters
Nov 14, 2025
-
Why Are Substances Able To Diffuse Through The Capillaries
Nov 14, 2025
-
What Kind Of Bonds Hold Amino Acids Together
Nov 14, 2025
-
Difference Between Adaptation And Natural Selection
Nov 14, 2025
-
A Metric Unit Of Measurement For Volume
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about 6 - 1 X 0 + 2 / 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.