5/8 As A Percent And Decimal
pythondeals
Nov 21, 2025 · 9 min read
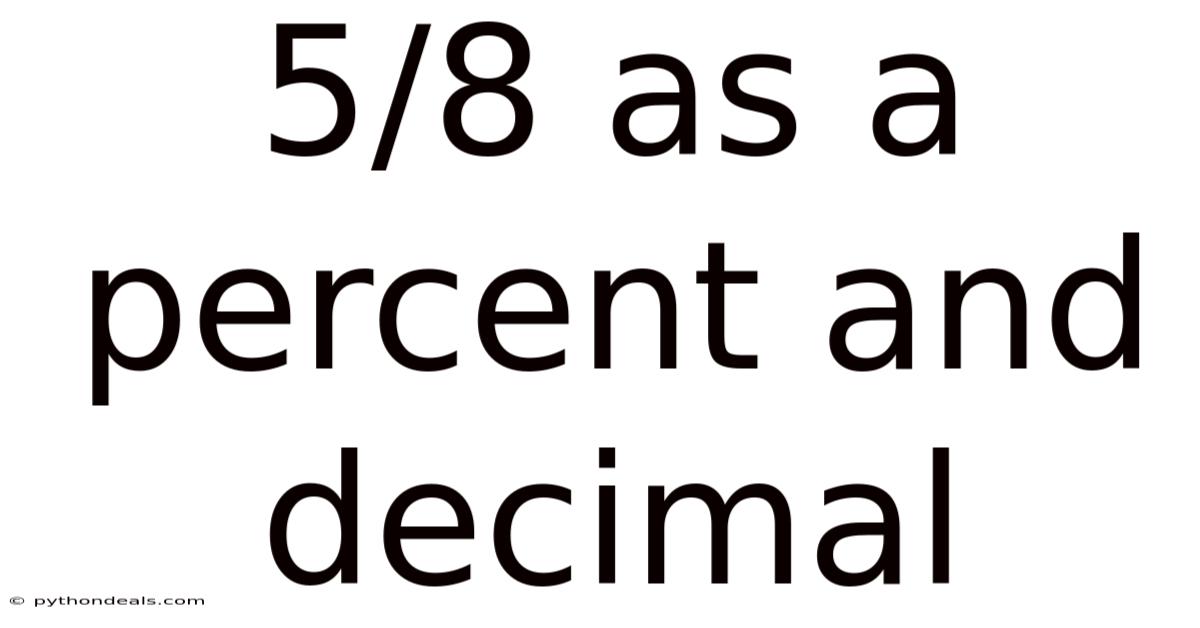
Table of Contents
Navigating fractions, percentages, and decimals can sometimes feel like traversing a complex maze. However, understanding how these concepts relate to each other is a fundamental skill in mathematics. Today, we're going to demystify the fraction 5/8, exploring how to convert it into both a percentage and a decimal. Whether you're a student brushing up on your math skills or just curious about numbers, this comprehensive guide will provide you with clear, step-by-step instructions and valuable insights.
Understanding the Basics
Before we dive into the specifics of converting 5/8, let's quickly review the basic concepts of fractions, decimals, and percentages.
- Fraction: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The fraction 5/8 means we have 5 parts out of a total of 8 equal parts.
- Decimal: A decimal is another way of representing a fraction. It uses a base-10 system, where numbers to the right of the decimal point represent fractional parts of 1. For example, 0.5 represents one-half.
- Percentage: A percentage is a way of expressing a number as a fraction of 100. The term "percent" means "per hundred." So, 50% means 50 out of 100.
Converting 5/8 to a Decimal
The most straightforward method to convert a fraction to a decimal is by dividing the numerator by the denominator. In this case, we need to divide 5 by 8.
Step-by-Step Guide:
- Set up the division: Write the division problem as 5 ÷ 8.
- Perform the division: Since 5 is smaller than 8, we need to add a decimal point and a zero to 5, making it 5.0. Now we divide 5.0 by 8.
- Divide:
- 8 goes into 50 six times (6 x 8 = 48).
- Subtract 48 from 50, which leaves 2.
- Add another zero to the dividend, making it 20.
- 8 goes into 20 two times (2 x 8 = 16).
- Subtract 16 from 20, which leaves 4.
- Add another zero, making it 40.
- 8 goes into 40 exactly five times (5 x 8 = 40).
- Subtract 40 from 40, which leaves 0.
Therefore, 5 ÷ 8 = 0.625.
Result: 5/8 as a decimal is 0.625.
Converting 5/8 to a Percentage
To convert a fraction to a percentage, you first convert the fraction to a decimal (as shown above) and then multiply the decimal by 100. This is because a percentage represents a fraction out of 100.
Step-by-Step Guide:
-
Convert to decimal: As we've already determined, 5/8 = 0.625.
-
Multiply by 100: Multiply 0.625 by 100 to convert it to a percentage.
-
- 625 x 100 = 62.5
-
-
Add the percent sign: Affix the percent sign (%) to the result.
Result: 5/8 as a percentage is 62.5%.
Comprehensive Overview of Fractions, Decimals, and Percentages
To fully grasp the conversion process, it's helpful to understand the broader context of fractions, decimals, and percentages. These are different ways of representing the same underlying value, and the ability to convert between them is crucial in various mathematical applications.
Fractions
A fraction is a way to represent a part of a whole. It is written as a ratio of two numbers, the numerator and the denominator.
- Numerator: The top number in a fraction, representing the number of parts we have.
- Denominator: The bottom number in a fraction, representing the total number of equal parts that make up the whole.
Fractions can be classified into several types:
- Proper Fractions: The numerator is less than the denominator (e.g., 1/2, 3/4, 5/8).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 5/3, 8/8, 11/4).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 2/3, 3 1/4).
Decimals
A decimal is a way to represent numbers using a base-10 system. Each position to the right of the decimal point represents a fraction with a denominator that is a power of 10.
- Tenths: The first digit to the right of the decimal point represents tenths (e.g., 0.1 = 1/10).
- Hundredths: The second digit represents hundredths (e.g., 0.01 = 1/100).
- Thousandths: The third digit represents thousandths (e.g., 0.001 = 1/1000).
Decimals can be terminating (ending) or repeating:
- Terminating Decimals: Decimals that have a finite number of digits (e.g., 0.5, 0.25, 0.625).
- Repeating Decimals: Decimals that have a pattern of digits that repeats indefinitely (e.g., 0.333..., 0.142857142857...).
Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "per hundred."
- Understanding Percentages: A percentage is always out of 100. For example, 75% means 75 out of 100.
- Converting to and from Percentages: To convert a decimal to a percentage, multiply by 100. To convert a percentage to a decimal, divide by 100.
Historical Context
The concepts of fractions, decimals, and percentages have evolved over centuries, playing a crucial role in mathematics, commerce, and science.
- Fractions: Ancient civilizations, including the Egyptians and Babylonians, used fractions extensively. The Egyptians used unit fractions (fractions with a numerator of 1), while the Babylonians used a base-60 system, which allowed for more complex fractional calculations.
- Decimals: Decimals were independently developed in China and Europe. The Chinese used decimal fractions as early as the 3rd century AD, while the European development is attributed to Simon Stevin in the late 16th century.
- Percentages: The concept of percentages emerged in ancient Rome, where taxes were often calculated as a percentage of assets. However, the modern notation of using the percent sign (%) developed much later.
Tren & Perkembangan Terbaru
In today's digital age, understanding fractions, decimals, and percentages remains essential, with numerous applications in finance, statistics, and everyday problem-solving. Current trends include:
- Financial Literacy: Emphasis on understanding percentages in personal finance, such as interest rates, discounts, and investment returns.
- Data Analysis: Use of decimals and percentages in statistical analysis to interpret and present data effectively.
- E-commerce: Application of percentages in online retail for calculating discounts, sales tax, and profit margins.
- Education: Innovative teaching methods to help students grasp these concepts, using visual aids, interactive tools, and real-world examples.
Tips & Expert Advice
Here are some expert tips to help you master the conversion of fractions to decimals and percentages:
- Memorize Common Conversions: Familiarize yourself with common fraction-decimal-percentage equivalents, such as 1/2 = 0.5 = 50%, 1/4 = 0.25 = 25%, and 3/4 = 0.75 = 75%. This can save time and improve accuracy.
- Practice Regularly: Consistent practice is key to mastering these conversions. Work through various examples and exercises to reinforce your understanding.
- Use Visual Aids: Utilize visual aids like pie charts or number lines to understand the relationship between fractions, decimals, and percentages. This can make the concepts more intuitive.
- Apply Real-World Examples: Relate these concepts to real-world situations. For example, calculate discounts at a store or determine the percentage of a sports team's wins.
- Understand the Underlying Logic: Instead of just memorizing formulas, try to understand the reasoning behind the conversions. This will help you apply the concepts in different contexts.
Practical Applications
Understanding how to convert fractions to decimals and percentages has numerous practical applications in everyday life. Here are a few examples:
- Cooking: Recipes often use fractions to specify ingredient quantities. Converting these fractions to decimals or percentages can help you scale recipes up or down.
- Shopping: Calculating discounts and sales tax involves converting percentages to decimals to determine the final price of an item.
- Finance: Understanding interest rates and investment returns requires proficiency in converting between fractions, decimals, and percentages.
- Construction: Measurements in construction often involve fractions. Converting these fractions to decimals can simplify calculations and ensure accuracy.
- Data Analysis: Interpreting statistical data often involves converting fractions or decimals to percentages to understand proportions and trends.
Common Mistakes to Avoid
When converting fractions to decimals and percentages, it's important to avoid common mistakes that can lead to incorrect answers. Here are a few pitfalls to watch out for:
- Incorrect Division: Make sure to divide the numerator by the denominator correctly. Double-check your work to avoid errors.
- Misplacing the Decimal Point: Ensure that you place the decimal point correctly when converting to a decimal. A misplaced decimal point can significantly alter the value of the number.
- Forgetting to Multiply by 100: When converting a decimal to a percentage, remember to multiply by 100. Forgetting this step will result in an incorrect percentage.
- Rounding Errors: Be mindful of rounding errors when dealing with decimals. Round to the appropriate number of decimal places to maintain accuracy.
- Confusing Numerator and Denominator: Always remember that the numerator is divided by the denominator. Mixing these up will lead to an incorrect result.
FAQ (Frequently Asked Questions)
Q: How do I convert a mixed number to a decimal?
A: First, convert the mixed number to an improper fraction. Then, divide the numerator by the denominator to get the decimal.
Q: Can all fractions be converted to terminating decimals?
A: No, only fractions whose denominators have prime factors of 2 and/or 5 can be converted to terminating decimals.
Q: How do I convert a repeating decimal to a fraction?
A: This process involves algebraic manipulation. For example, if x = 0.333..., then 10x = 3.333.... Subtracting x from 10x gives 9x = 3, so x = 3/9 = 1/3.
Q: Why is understanding percentages important?
A: Percentages are used extensively in finance, statistics, and everyday life. Understanding percentages is essential for making informed decisions about money, interpreting data, and understanding proportions.
Q: Is there an easier way to convert fractions to percentages without using a calculator?
A: Yes, if you can simplify the fraction to have a denominator of 100, the numerator will be the percentage. For example, 20/50 can be simplified to 40/100, which is 40%.
Conclusion
Converting fractions to decimals and percentages is a fundamental skill that has wide-ranging applications. By understanding the underlying concepts and following the step-by-step guides provided in this article, you can confidently perform these conversions and apply them in various contexts. Remember to practice regularly, use visual aids, and relate these concepts to real-world examples to reinforce your understanding.
So, how do you feel about tackling fractions, decimals, and percentages now? Are you ready to put these steps into practice and see how they can simplify your daily calculations?
Latest Posts
Latest Posts
-
Social Structure In Old Kingdom Egypt
Nov 21, 2025
-
How To Calculate Upper And Lower Bounds
Nov 21, 2025
-
What Are The 4 Types Of Fossils
Nov 21, 2025
-
Write The Equation Of A Parabola In Vertex Form
Nov 21, 2025
-
How Do You Draw An Ion
Nov 21, 2025
Related Post
Thank you for visiting our website which covers about 5/8 As A Percent And Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.