2 3 X 2 9 As A Fraction
pythondeals
Nov 06, 2025 · 9 min read
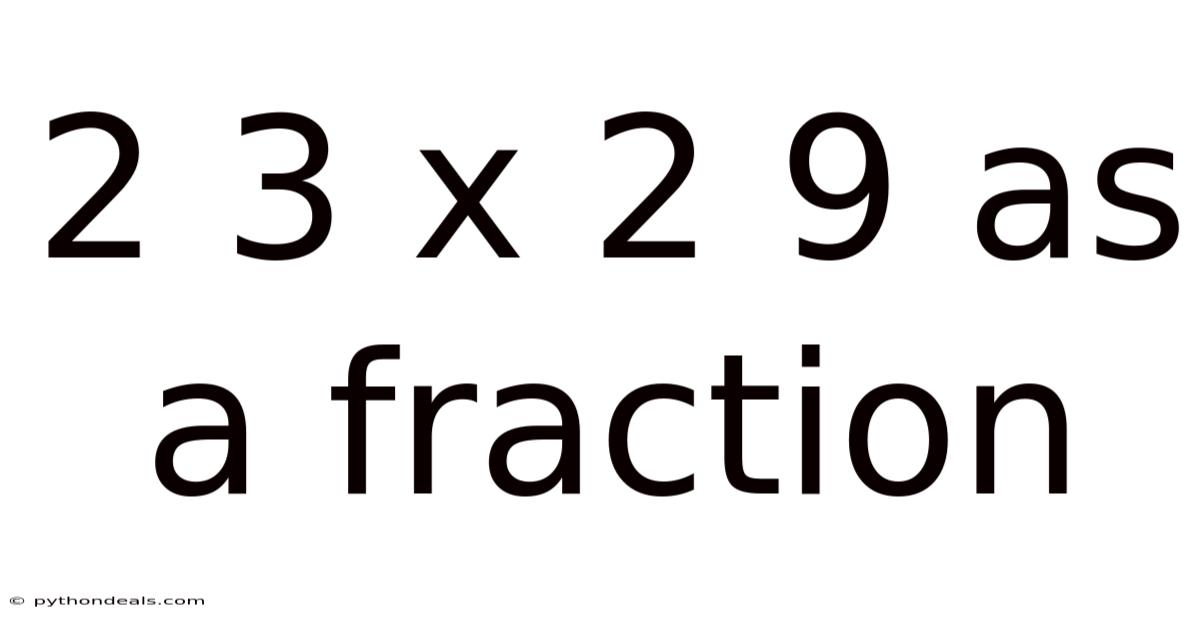
Table of Contents
Navigating the World of Fractions: Expressing 2.3 x 2.9
The world of mathematics is filled with fascinating concepts, and fractions are undoubtedly one of the most fundamental. Fractions help us understand parts of a whole, express ratios, and perform various calculations. Among the myriad of operations we can perform with fractions, converting decimal products into fractional form is particularly useful. In this comprehensive guide, we will explore how to express the product of 2.3 and 2.9 as a fraction. We will delve into the step-by-step process, providing clear explanations and examples to ensure a thorough understanding.
Multiplying Decimals: A Foundation Before we dive into converting the product of 2.3 and 2.9 into a fraction, it is essential to understand how to multiply decimals. Multiplying decimals involves a few key steps:
Remove the Decimal Points: Initially, treat the decimals as whole numbers. This means you would multiply 23 and 29 as if they were integers.
Perform the Multiplication: Multiply the two whole numbers using standard multiplication techniques.
Place the Decimal Point: Count the total number of decimal places in the original numbers. In this case, 2.3 has one decimal place, and 2.9 has one decimal place, totaling two decimal places. Place the decimal point in the product so that there are two decimal places from the right.
Step-by-Step Calculation of 2.3 x 2.9 Let's walk through the multiplication of 2.3 and 2.9 step-by-step:
Remove the Decimal Points: Treat 2.3 as 23 and 2.9 as 29.
Multiply the Whole Numbers: Multiply 23 by 29:
23 x 29 = 667
Place the Decimal Point: Since there is a total of two decimal places in the original numbers (one in 2.3 and one in 2.9), we place the decimal point two places from the right in the product.
667 becomes 6.67
So, 2.3 x 2.9 = 6.67.
Understanding Fractions Now that we have the decimal product, we can convert it into a fraction. A fraction represents a part of a whole and is expressed as a numerator over a denominator. The numerator indicates how many parts of the whole you have, and the denominator indicates the total number of parts that make up the whole.
Converting Decimals to Fractions Converting a decimal to a fraction involves the following steps:
Identify the Decimal Places: Determine the number of decimal places in the decimal. This will help you determine the denominator of the fraction.
Write the Decimal as a Fraction: Write the decimal as a fraction with the decimal number as the numerator and a power of 10 as the denominator. The power of 10 corresponds to the number of decimal places. For example, if there are two decimal places, the denominator will be 100.
Simplify the Fraction: Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD). This ensures that the fraction is in its simplest form.
Converting 6.67 to a Fraction Let's convert 6.67 to a fraction:
Identify the Decimal Places: 6.67 has two decimal places.
Write the Decimal as a Fraction: Write 6.67 as a fraction with 667 as the numerator and 100 as the denominator:
6.67 = 667/100
Simplify the Fraction: In this case, 667 and 100 do not have any common factors other than 1. Therefore, the fraction 667/100 is already in its simplest form.
Expressing 667/100 as a Mixed Number While 667/100 is a valid fraction, it is an improper fraction (the numerator is greater than the denominator). It can also be expressed as a mixed number, which consists of a whole number and a proper fraction.
To convert an improper fraction to a mixed number:
Divide the Numerator by the Denominator: Divide 667 by 100.
Identify the Whole Number and Remainder: The quotient (the result of the division) will be the whole number, and the remainder will be the numerator of the fractional part. The denominator remains the same.
Converting 667/100 to a Mixed Number Divide 667 by 100:
667 ÷ 100 = 6 with a remainder of 67
So, 667/100 as a mixed number is:
6 67/100
Thus, 2.3 x 2.9 can be expressed as the fraction 667/100 or the mixed number 6 67/100.
Detailed Explanation of Decimal Multiplication To reinforce our understanding, let's explore the concept of decimal multiplication more deeply.
Understanding Decimal Places: Each decimal place represents a fraction with a power of 10 as the denominator. For example:
0.1 = 1/10 0.01 = 1/100 0.001 = 1/1000
When multiplying decimals, you are essentially multiplying fractions. For instance:
2.3 x 2.9 = (23/10) x (29/10)
Multiplying the numerators and denominators gives:
(23 x 29) / (10 x 10) = 667 / 100
This illustrates why we count the decimal places and place the decimal point accordingly in the final product.
Alternative Method for Decimal Multiplication Another way to approach decimal multiplication is by using the distributive property:
2.3 x 2.9 = (2 + 0.3) x (2 + 0.9)
Using the distributive property:
(2 x 2) + (2 x 0.9) + (0.3 x 2) + (0.3 x 0.9) = 4 + 1.8 + 0.6 + 0.27 = 6.67
This method breaks down the multiplication into smaller, more manageable parts, which can be particularly useful for mental calculations or when dealing with more complex decimals.
Simplifying Fractions: A Deeper Dive Simplifying fractions is an essential skill in mathematics. A fraction is in its simplest form when the numerator and denominator have no common factors other than 1.
Finding the Greatest Common Divisor (GCD): The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder. There are several methods to find the GCD, including:
Listing Factors: List all the factors of both numbers and identify the largest factor they have in common.
Euclidean Algorithm: The Euclidean algorithm is an efficient method for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The GCD is the last non-zero remainder.
Example: Finding the GCD of 667 and 100 In our case, we need to find the GCD of 667 and 100 to determine if the fraction 667/100 can be simplified.
Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100 Factors of 667: 1, 23, 29, 667
The only common factor between 667 and 100 is 1. Therefore, the GCD is 1, and the fraction 667/100 is already in its simplest form.
Converting Improper Fractions to Mixed Numbers: A Detailed Look Converting an improper fraction to a mixed number involves dividing the numerator by the denominator and expressing the result as a whole number and a proper fraction.
Understanding the Process: When you divide the numerator by the denominator, the quotient represents the number of whole units, and the remainder represents the fractional part. The denominator of the fractional part remains the same as the original denominator.
Example: Converting 667/100 to a Mixed Number Divide 667 by 100:
667 ÷ 100 = 6 with a remainder of 67
The quotient is 6, which is the whole number part of the mixed number. The remainder is 67, which is the numerator of the fractional part. The denominator remains 100.
So, 667/100 as a mixed number is:
6 67/100
Practical Applications Understanding how to convert decimal products into fractions has numerous practical applications in various fields, including:
Finance: In financial calculations, decimals are often used to represent interest rates, percentages, and monetary values. Converting these decimals to fractions can simplify calculations and provide a clearer understanding of the relationships between different quantities.
Engineering: Engineers frequently work with decimals in measurements and calculations. Converting these decimals to fractions can help in precise calculations and in expressing measurements in a more standardized form.
Science: Scientists use decimals to represent experimental data and results. Converting decimals to fractions can aid in data analysis and in comparing different values.
Everyday Life: In everyday situations, such as cooking, baking, and measuring, decimals are commonly used. Converting these decimals to fractions can simplify recipes and ensure accurate measurements.
Conclusion Converting the product of decimals, such as 2.3 x 2.9, into a fraction is a valuable skill that combines the principles of decimal multiplication and fraction conversion. By following the step-by-step process outlined in this guide, you can confidently express any decimal product as a fraction in its simplest form. Whether you are a student, a professional, or simply someone who enjoys working with numbers, mastering this skill will enhance your mathematical abilities and provide you with a deeper understanding of fractions. Understanding how to perform this conversion not only solidifies your grasp on fundamental mathematical concepts but also equips you with a versatile tool applicable in a wide array of practical scenarios. Whether you choose to represent 2.3 x 2.9 as the improper fraction 667/100 or the mixed number 6 67/100, you are accurately conveying the same value in different but equally valid forms. This exercise underscores the importance of flexibility and precision in mathematical operations, reinforcing the idea that numbers can be represented and manipulated in various ways to suit different contexts and purposes.
Frequently Asked Questions (FAQ)
Q: Why is it important to convert decimals to fractions? A: Converting decimals to fractions can simplify calculations, provide a clearer understanding of the relationships between quantities, and ensure accurate measurements in various applications.
Q: How do I convert a decimal to a fraction? A: Write the decimal as a fraction with the decimal number as the numerator and a power of 10 as the denominator, then simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (GCD).
Q: What is the greatest common divisor (GCD)? A: The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder.
Q: How do I find the GCD of two numbers? A: You can find the GCD by listing factors, using the Euclidean algorithm, or other methods.
Q: How do I convert an improper fraction to a mixed number? A: Divide the numerator by the denominator. The quotient is the whole number, and the remainder is the numerator of the fractional part, with the denominator remaining the same.
Q: Can all fractions be simplified? A: No, a fraction can only be simplified if the numerator and denominator have common factors other than 1. If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form.
Q: Are mixed numbers and improper fractions interchangeable? A: Yes, mixed numbers and improper fractions are different ways of representing the same value. You can convert between them as needed.
Q: Is it possible to convert a repeating decimal to a fraction? A: Yes, it is possible to convert a repeating decimal to a fraction, but the process is slightly different from converting a terminating decimal. It involves setting up an equation and solving for the fraction.
Latest Posts
Latest Posts
-
What Is The Difference Between Sympatric And Allopatric Speciation
Nov 06, 2025
-
What Are The 3 Basic Parts Of An Atom
Nov 06, 2025
-
Is Wedge Up Or Down Chemistry
Nov 06, 2025
-
What Is The Difference Between Celsius And Fahrenheit
Nov 06, 2025
-
What Is The Asthenosphere Composed Of
Nov 06, 2025
Related Post
Thank you for visiting our website which covers about 2 3 X 2 9 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.