1/4 Plus 1/4 Plus 1/4 Equals
pythondeals
Nov 17, 2025 · 9 min read
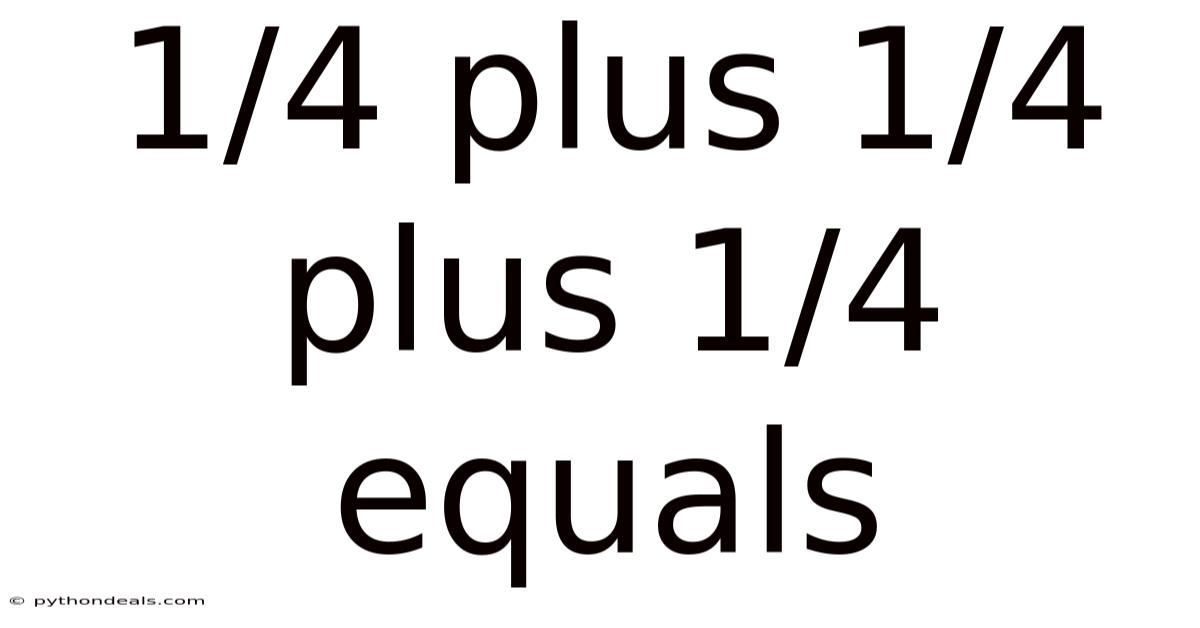
Table of Contents
Let's dive into a seemingly simple yet fundamental mathematical concept: adding fractions. Specifically, let's explore what happens when you add 1/4 plus 1/4 plus 1/4. While the answer might seem obvious (and indeed, it is!), the process and the implications extend far beyond basic arithmetic. Understanding how to add fractions is crucial for various applications in everyday life, from cooking and baking to managing finances and understanding proportions. So, let's embark on this mathematical journey, uncovering the nuances and practical uses of adding these fractions together.
Understanding fractions is essential for grasping more complex mathematical concepts. A fraction represents a part of a whole. In the fraction 1/4, the '1' is the numerator, representing the number of parts we have, and the '4' is the denominator, representing the total number of equal parts that make up the whole. Therefore, 1/4 signifies one part out of four equal parts. Adding fractions involves combining these parts to determine the total fraction of the whole we have. In the case of 1/4 + 1/4 + 1/4, we are simply adding the numerators together while keeping the denominator the same, since the denominators are already common. This leads to a straightforward and intuitive result. But let's not stop there; let's delve deeper into the mechanics and applications of this simple addition.
The Mechanics of Adding 1/4 + 1/4 + 1/4
Adding fractions is relatively straightforward when the fractions share a common denominator, as is the case with 1/4 + 1/4 + 1/4. The process involves the following steps:
-
Identify the Common Denominator: In this case, the denominator for all three fractions is 4. This means that each fraction represents a portion of a whole divided into four equal parts.
-
Add the Numerators: Since the denominators are the same, you simply add the numerators together. So, 1 + 1 + 1 = 3.
-
Write the Result: The sum of the numerators becomes the new numerator, and the common denominator remains the same. Therefore, 1/4 + 1/4 + 1/4 = 3/4.
Thus, 1/4 + 1/4 + 1/4 equals 3/4. This means that you have three out of four equal parts of a whole. It’s a simple operation, but it’s the foundation for more complex fractional arithmetic. To solidify this concept, let's visualize it. Imagine a pie cut into four equal slices. If you have one slice (1/4), and then you get another slice (1/4), and finally a third slice (1/4), you now have three slices out of the four, which is 3/4 of the pie.
Comprehensive Overview: Fractions and Their Significance
Fractions are a fundamental part of mathematics and are used extensively in various real-world applications. Understanding fractions involves grasping several key concepts:
-
Types of Fractions: Fractions can be categorized into different types, including:
- Proper Fractions: These are fractions where the numerator is less than the denominator, such as 1/2, 3/4, and 5/8. Proper fractions represent a value less than one whole.
- Improper Fractions: These are fractions where the numerator is greater than or equal to the denominator, such as 5/4, 7/3, and 8/8. Improper fractions represent a value equal to or greater than one whole.
- Mixed Numbers: These consist of a whole number and a proper fraction, such as 1 1/2, 2 3/4, and 3 1/4. Mixed numbers are another way to represent values greater than one.
-
Equivalent Fractions: Equivalent fractions are different fractions that represent the same value. For example, 1/2 is equivalent to 2/4, 3/6, and 4/8. You can create equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number.
-
Simplifying Fractions: Simplifying fractions involves reducing them to their simplest form by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, the fraction 4/8 can be simplified to 1/2 by dividing both the numerator and the denominator by 4.
-
Adding and Subtracting Fractions: As we've already seen, adding and subtracting fractions with a common denominator is straightforward. However, when fractions have different denominators, you need to find a common denominator before performing the addition or subtraction. This involves finding the least common multiple (LCM) of the denominators.
-
Multiplying Fractions: Multiplying fractions involves multiplying the numerators together and multiplying the denominators together. For example, 1/2 * 2/3 = (1 * 2) / (2 * 3) = 2/6, which can be simplified to 1/3.
-
Dividing Fractions: Dividing fractions involves multiplying the first fraction by the reciprocal of the second fraction. For example, 1/2 ÷ 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4.
Fractions are not just abstract mathematical concepts; they are integral to many aspects of our daily lives. From measuring ingredients in a recipe to calculating discounts while shopping, fractions are essential tools that help us navigate the world around us. Understanding the basics of fractions, including how to add, subtract, multiply, and divide them, empowers us to make informed decisions and solve practical problems.
Tren & Perkembangan Terbaru
While the basic principles of adding fractions remain constant, their application in modern contexts is continually evolving. Here are a few current trends and developments:
-
Educational Technology: Technology is transforming how fractions are taught and learned. Interactive apps, online games, and virtual manipulatives make it easier for students to visualize and understand fractional concepts. These tools often provide immediate feedback, personalized learning paths, and engaging challenges that enhance the learning experience.
-
Data Analysis: In data science and statistics, fractions are often used to represent proportions and percentages. Understanding how to manipulate fractions is crucial for analyzing datasets, interpreting statistical results, and making informed decisions based on data.
-
Financial Literacy: Fractions play a significant role in financial literacy. Understanding interest rates, loan terms, and investment returns often involves working with fractions and percentages. A solid grasp of fractional concepts can help individuals make sound financial decisions and manage their money effectively.
-
Cooking and Baking: Chefs and bakers rely heavily on fractions to accurately measure ingredients and scale recipes. Whether it's halving a recipe or doubling it, a solid understanding of fractions is essential for consistent and delicious results.
-
Construction and Engineering: Fractions are essential in construction and engineering for measuring lengths, calculating areas, and determining proportions. Accurate fractional calculations are critical for ensuring structural integrity and precision in building projects.
The ongoing development of technology and the increasing emphasis on data-driven decision-making highlight the continued importance of understanding fractions in various professional fields and everyday situations.
Tips & Expert Advice
To master the art of adding fractions and applying them effectively, consider these tips and expert advice:
-
Visualize Fractions: Use visual aids such as fraction bars, pie charts, or number lines to help you understand and compare fractions. Visualization can make abstract concepts more concrete and easier to grasp. For example, when adding 1/4 + 1/4 + 1/4, picture three slices of a pie, each representing one-quarter of the pie. Combining these slices visually reinforces the concept that you now have three-quarters of the pie.
-
Practice Regularly: Like any mathematical skill, proficiency in fractions requires consistent practice. Work through a variety of problems, starting with simple examples and gradually progressing to more complex ones. Regular practice will help you build confidence and improve your speed and accuracy. Use online resources, textbooks, or worksheets to find practice problems.
-
Understand Equivalent Fractions: Mastering equivalent fractions is crucial for adding and subtracting fractions with different denominators. Learn how to find equivalent fractions by multiplying or dividing both the numerator and the denominator by the same number. This skill will enable you to rewrite fractions with a common denominator, making addition and subtraction much easier.
-
Simplify Your Answers: Always simplify your answers to their simplest form. Simplifying fractions involves dividing both the numerator and the denominator by their greatest common divisor (GCD). This ensures that your answers are expressed in the most concise and easily understandable manner. For example, if you arrive at an answer of 2/4, simplify it to 1/2.
-
Apply Fractions to Real-World Problems: Look for opportunities to apply your knowledge of fractions to real-world situations. This will help you understand the practical relevance of fractions and make the learning process more engaging. For example, when cooking, practice doubling or halving recipes that involve fractional measurements. Or, when shopping, calculate discounts and sales taxes using fractions and percentages.
-
Use Technology Wisely: Take advantage of technology to enhance your learning experience. There are many excellent apps and websites that offer interactive lessons, practice problems, and helpful resources for learning about fractions. However, be mindful of relying too heavily on technology; it's essential to develop a solid understanding of the underlying concepts and be able to solve problems manually as well.
FAQ (Frequently Asked Questions)
Q: What is a fraction? A: A fraction represents a part of a whole. It consists of a numerator (the number of parts you have) and a denominator (the total number of equal parts that make up the whole).
Q: How do you add fractions with a common denominator? A: To add fractions with a common denominator, simply add the numerators together and keep the denominator the same.
Q: What do you do if fractions have different denominators? A: If fractions have different denominators, you need to find a common denominator before adding or subtracting them. This involves finding the least common multiple (LCM) of the denominators.
Q: What is an equivalent fraction? A: Equivalent fractions are different fractions that represent the same value. For example, 1/2 is equivalent to 2/4, 3/6, and 4/8.
Q: How do you simplify a fraction? A: To simplify a fraction, divide both the numerator and the denominator by their greatest common divisor (GCD).
Q: Why are fractions important? A: Fractions are essential for various real-world applications, including cooking, baking, finance, construction, and data analysis. Understanding fractions empowers us to make informed decisions and solve practical problems.
Conclusion
In summary, 1/4 + 1/4 + 1/4 equals 3/4. While the arithmetic is simple, the underlying concepts of fractions are fundamental to mathematics and have widespread applications in everyday life. By understanding the mechanics of adding fractions, exploring their significance, staying abreast of current trends, and following expert advice, you can master this essential skill and apply it effectively in various contexts. From baking a cake to managing your finances, fractions are a valuable tool that can help you navigate the world around you.
Adding fractions, especially when they share a common denominator, is a foundational skill that unlocks doors to more complex mathematical concepts and practical applications. The ability to quickly and accurately add fractions, like 1/4 + 1/4 + 1/4, empowers individuals to make informed decisions in a variety of real-world scenarios. So, embrace the world of fractions, practice regularly, and discover the power of this essential mathematical tool!
How do you plan to incorporate your understanding of fractions into your daily life or professional endeavors? Are you interested in exploring more complex fractional arithmetic or delving into the applications of fractions in specific fields?
Latest Posts
Latest Posts
-
What Is Micro And Macro Economics
Nov 17, 2025
-
Micro Mezzo And Macro Levels Of Social Work
Nov 17, 2025
-
What Is A One Solution In Math
Nov 17, 2025
-
What Is The Ph Value Of Lemon
Nov 17, 2025
-
Ammonium Chloride Is Acid Or Base
Nov 17, 2025
Related Post
Thank you for visiting our website which covers about 1/4 Plus 1/4 Plus 1/4 Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.