1 3 X 2 3 X 1 2
pythondeals
Nov 02, 2025 · 9 min read
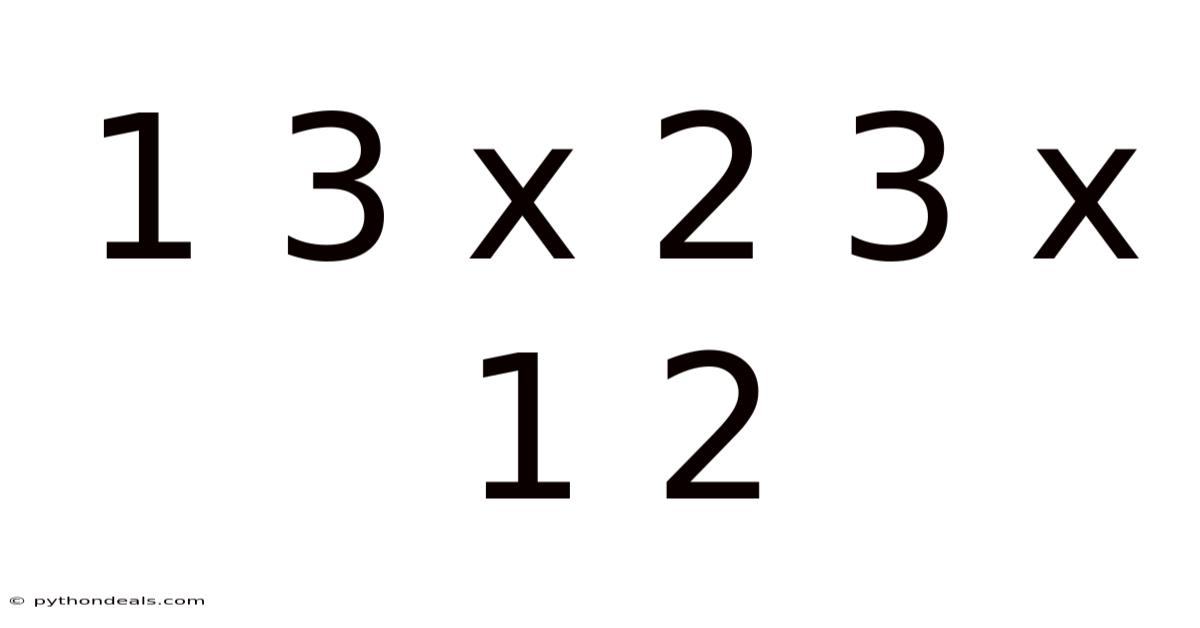
Table of Contents
Let's delve into the fascinating world of fractions and explore the multiplication of three specific fractions: 1/3, 2/3, and 1/2. While it may seem like a simple arithmetic problem, understanding the underlying principles and applications of fraction multiplication is crucial for various fields, from cooking and baking to engineering and finance. This article will provide a comprehensive breakdown of the concept, step-by-step calculations, real-world examples, and frequently asked questions to solidify your understanding.
Introduction
Fractions are a fundamental part of mathematics, representing parts of a whole. They are used daily in various contexts, from dividing a pizza equally among friends to calculating proportions in recipes. Understanding how to perform operations with fractions, such as multiplication, is essential for navigating these everyday situations and more complex mathematical problems. The expression 1/3 x 2/3 x 1/2 represents the multiplication of three fractions, each representing a different proportion. Let's break down what this means and how to solve it.
Understanding Fractions: A Quick Recap
Before we jump into the multiplication, let's refresh our understanding of what fractions are. A fraction consists of two parts:
- Numerator: The top number, which represents the number of parts we have.
- Denominator: The bottom number, which represents the total number of equal parts the whole is divided into.
For instance, in the fraction 1/3, 1 is the numerator (the number of parts we have), and 3 is the denominator (the total number of parts the whole is divided into). It signifies that we have one part out of three equal parts.
Fraction Multiplication: The Basics
Multiplying fractions is straightforward. The basic rule is: multiply the numerators together and multiply the denominators together.
Mathematically:
(a/b) x (c/d) = (a x c) / (b x d)
Where 'a' and 'c' are numerators, and 'b' and 'd' are denominators.
Applying the Rule to 1/3 x 2/3 x 1/2
Now, let's apply this rule to our specific problem: 1/3 x 2/3 x 1/2.
-
Step 1: Multiply the Numerators:
Multiply all the numerators together: 1 x 2 x 1 = 2
-
Step 2: Multiply the Denominators:
Multiply all the denominators together: 3 x 3 x 2 = 18
-
Step 3: Form the Resulting Fraction:
Combine the results to form the new fraction: 2/18
-
Step 4: Simplify the Fraction (if possible):
The fraction 2/18 can be simplified. Both the numerator and the denominator are divisible by 2.
2 ÷ 2 = 1
18 ÷ 2 = 9
So, the simplified fraction is 1/9.
Therefore, 1/3 x 2/3 x 1/2 = 1/9.
Comprehensive Overview: Why Does This Work?
Understanding why multiplying fractions works this way is crucial for a deeper understanding. Think of fractions as operators that scale down a whole.
Let's visualize it:
- 1/3: Imagine a pie cut into three equal slices. 1/3 represents one of those slices.
- 2/3: Imagine the same pie cut into three equal slices. 2/3 represents two of those slices.
- 1/2: Imagine a different pie cut into two equal slices. 1/2 represents one of those slices.
Now, multiplying these fractions together can be visualized as taking a fraction of a fraction.
- 1/3 x 2/3: This means taking 1/3 of 2/3. In other words, we're finding a portion of the 2/3 of the pie we already have.
- (1/3 x 2/3) x 1/2: This then means taking 1/2 of the result we got from multiplying 1/3 and 2/3.
By multiplying numerators and denominators, we're essentially finding a smaller and smaller portion of the original whole. This concept is fundamental in understanding ratios, proportions, and scaling in mathematics.
Real-World Applications of Fraction Multiplication
The multiplication of fractions isn't just an abstract mathematical concept; it has numerous practical applications in everyday life. Here are a few examples:
-
Cooking and Baking:
- Scaling Recipes: If a recipe calls for 1/2 cup of flour but you only want to make half the recipe, you would multiply 1/2 by 1/2 to find the new amount of flour needed (1/4 cup).
- Adjusting Ingredients: Suppose a cake recipe requires 2/3 cup of sugar, but you want to make 3/4 of the cake. You'd multiply 2/3 by 3/4 to determine the adjusted amount of sugar.
-
Construction and Engineering:
- Calculating Materials: Architects and engineers frequently use fractions to calculate material requirements. For instance, determining the length of a beam that is 1/4 the length of a 2/3 meter section.
- Measuring Dimensions: Precisely measuring dimensions and cuts is critical in construction. Multiplying fractions helps in calculating the required dimensions for various components.
-
Finance and Business:
- Calculating Discounts: If an item is 1/3 off and you have a coupon for an additional 1/2 off, you would need to multiply the fractions to determine the total discount percentage.
- Calculating Profits: In business, profits are often calculated as a fraction of revenue. Multiplying these fractions helps in determining various financial metrics.
-
Time Management:
- Allocating Time: If you allocate 1/2 of your day to work and then spend 2/3 of that time on a specific project, multiplying these fractions tells you what fraction of your day is spent on that project (1/2 x 2/3 = 1/3 of the day).
These examples demonstrate the versatility and importance of fraction multiplication in diverse real-world contexts.
Tren & Perkembangan Terbaru
While the basic principles of fraction multiplication remain constant, its application in technology and data analysis is evolving.
- Algorithmic Trading: Financial algorithms use complex calculations involving fractions to make split-second decisions in stock trading. High-frequency trading relies heavily on these fractional calculations.
- Data Science and Machine Learning: In data science, fractional values are used to represent probabilities, weights, and scaling factors in machine learning models. Understanding fraction multiplication is crucial for building accurate and efficient models.
- Computer Graphics: Computer graphics use fractions extensively for scaling, rotating, and transforming objects in 3D space. Fractional arithmetic is fundamental for creating realistic visual effects.
The digital age has amplified the importance of understanding and applying fractional calculations in these advanced fields.
Tips & Expert Advice
Here are some tips and expert advice to help you master fraction multiplication:
-
Simplify Before Multiplying:
Sometimes, you can simplify fractions before multiplying to make the calculation easier. For example, if you have (2/4) x (1/2), you can simplify 2/4 to 1/2 first. This results in (1/2) x (1/2), which is easier to calculate.
-
Convert Mixed Numbers to Improper Fractions:
If you encounter mixed numbers (e.g., 1 1/2), convert them to improper fractions before multiplying. To convert 1 1/2 to an improper fraction, multiply the whole number (1) by the denominator (2) and add the numerator (1), then place the result over the original denominator. So, 1 1/2 becomes (1x2 + 1)/2 = 3/2.
-
Use Visual Aids:
Visual aids such as fraction bars or pie charts can be incredibly helpful in understanding the concept of multiplying fractions. Draw diagrams to represent the fractions and visualize the multiplication process.
-
Practice Regularly:
Like any mathematical skill, practice is key. Work through various examples and problems to build your confidence and fluency in fraction multiplication.
-
Check Your Answers:
After multiplying and simplifying, always double-check your answer. Make sure the fraction is in its simplest form and that the result makes sense in the context of the problem.
-
Understand the "Of" Concept:
Remember that multiplication can be thought of as "of." So, 1/3 x 1/2 means "1/3 of 1/2." This conceptual understanding can make the process more intuitive.
-
Use Online Tools and Resources:
There are numerous online tools and resources available that can help you practice and learn fraction multiplication. Websites, apps, and video tutorials can provide valuable assistance.
-
Don't Fear the Complex Fractions: Even complex fractions can be solved by applying the same rules. Just break them down step by step and simplify as you go.
By following these tips and practicing consistently, you can become proficient in fraction multiplication and confidently apply it in various situations.
FAQ (Frequently Asked Questions)
Here are some frequently asked questions about fraction multiplication:
-
Q: Can I multiply more than two fractions at once?
- A: Yes, you can multiply any number of fractions by simply multiplying all the numerators together and all the denominators together. For example, 1/2 x 2/3 x 3/4 = (1 x 2 x 3) / (2 x 3 x 4) = 6/24 = 1/4.
-
Q: What happens if I multiply a fraction by a whole number?
- A: To multiply a fraction by a whole number, treat the whole number as a fraction with a denominator of 1. For example, 3 x 1/4 is the same as 3/1 x 1/4 = 3/4.
-
Q: Do I always need to simplify fractions after multiplying?
- A: It's best practice to always simplify fractions to their simplest form. This makes the fraction easier to understand and use in further calculations.
-
Q: What if I have a negative fraction?
- A: The rules for multiplying negative fractions are the same as for multiplying negative numbers. If you multiply a negative fraction by a positive fraction, the result is negative. If you multiply two negative fractions, the result is positive.
-
Q: Can I use a calculator to multiply fractions? A: Yes, many calculators have fraction functions, or you can convert the fractions to decimals and multiply. However, understanding the process is important for conceptual understanding.
Conclusion
Multiplying fractions like 1/3 x 2/3 x 1/2 is a fundamental skill with widespread applications. By understanding the basic principles, applying the multiplication rule, simplifying the results, and practicing regularly, you can master this skill and confidently use it in various real-world scenarios. Remember, fraction multiplication isn't just about numbers; it's about understanding proportions, scaling, and relationships between different parts of a whole. The answer to 1/3 x 2/3 x 1/2 is 1/9.
How do you plan to use your newfound knowledge of fraction multiplication in your daily life or work? Are you interested in exploring more complex fraction operations, such as division or addition?
Latest Posts
Related Post
Thank you for visiting our website which covers about 1 3 X 2 3 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.